Difference between revisions of "Place value activity 1"
CHaitra BS (talk | contribs) |
Gurumurthy (talk | contribs) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 10: | Line 10: | ||
==Prerequisites/Instructions, if any== | ==Prerequisites/Instructions, if any== | ||
==Multimedia resources== | ==Multimedia resources== | ||
| − | ==Website interactives/ links/ simulations== | + | ==Website interactives / links/ simulations== |
==Process (How to do the activity)== | ==Process (How to do the activity)== | ||
[[File:32 squares.png|400px|link=]] | [[File:32 squares.png|400px|link=]] | ||
| − | *Print 32 | + | *Above is a sheet with 10 vertical lines and 10 horizontal lines. Taken together, we can see 10 'cells' in each row and 10 'cells' in each column. |
| + | *Print 32 sheets of this '10 * 10' squares. | ||
*Distribute into 8 groups of 4 children each. | *Distribute into 8 groups of 4 children each. | ||
| − | *Each group will get 4 | + | *Each group will get 4 such sheets. |
*The value of 4 squares will be 4x100 = 400 | *The value of 4 squares will be 4x100 = 400 | ||
| − | *Each group | + | *Each group will cut the sheets such that |
| − | *Each one of those | + | *They can cut 2 sheets along the solid (darker / vertical) lines; here each sheet (10*10 square) will have 10 such "strips". These are "tens", each strip has 10 cells. So each square has 10 “tens” (They can either *cut, or work without cutting – up to the children) |
| + | *They can cut the other two sheets along both solid (darker / vertical) and the less dark / horizontal lines | ||
| + | *Each one of those sheets will have 100 cells | ||
| − | == Developmental | + | == Developmental points/questions == |
*Let the children make numbers and write them down | *Let the children make numbers and write them down | ||
*Ask them what is the largest number each group can make? 400 is the answer – but check if children understand this. | *Ask them what is the largest number each group can make? 400 is the answer – but check if children understand this. | ||
'''II. Abstraction from here (1 period)''' | '''II. Abstraction from here (1 period)''' | ||
| − | Now let us assume children have 9 such squares. | + | In the previous activity we gave 4 sheets to students to actually cut and play with. Now let us assume children have 9 such squares. |
In each group, how many hundreds are possible ? – 9 | In each group, how many hundreds are possible ? – 9 | ||
| Line 31: | Line 34: | ||
In each group, how many tens are there ? – 9 x 10 = 90 | In each group, how many tens are there ? – 9 x 10 = 90 | ||
| − | In each group, how many | + | In each group, how many ones are there ? – 90 x 10 = 900 |
'''1-9 ones are possible; 10 ones means one ten. Ten ones is the same as one ten''' | '''1-9 ones are possible; 10 ones means one ten. Ten ones is the same as one ten''' | ||
| Line 126: | Line 129: | ||
==Evaluation (Questions for assessment of the child)== | ==Evaluation (Questions for assessment of the child)== | ||
| + | #Making numbers | ||
| + | Suppose we have 4 digits 7, 8, 3, 5. We want to make different 4-digit numbers using these digits such that no digits are repeated in each number. For example, you can make 7835 and 3578 but 7738 is not allowed because 7 is repeated and 5 is not used. | ||
| + | |||
| + | a. What is the greatest number you can make? | ||
| + | |||
| + | b. What is the smallest number? | ||
| + | |||
| + | c. Can you write down how you make the greatest number and the smallest number? | ||
| + | |||
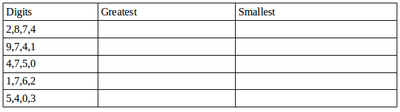
| + | Use the given digits without repetition and make the greatest and smallest 4-digit numbers. Note that 0753 is a 3 digit number and is therefore not allowed. | ||
| + | |||
| + | [[File:gretest and smallest.png|400px|link=]] | ||
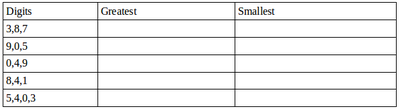
| + | #Now make the greatest and smallest 4-digit numbers by using any one digit twice. | ||
| + | Hint: Think about which digit you will use twice. | ||
| + | |||
| + | [[File:3 digit numbers.png|400px|link=]] | ||
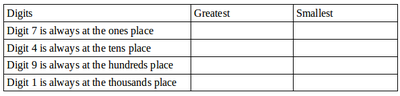
| + | #Make the greatest/ smallest 4-digit numbers using any 4 different digits with conditions as given | ||
| + | [[File:4 different digits.png|400px|link=]] | ||
| + | |||
==Question Corner== | ==Question Corner== | ||
==Activity Keywords== | ==Activity Keywords== | ||
'''To link back to the concept page''' | '''To link back to the concept page''' | ||
| − | + | ||
| − | [ | + | [[Category:Number system]] |
Latest revision as of 16:49, 28 January 2021
Activity - Making Hundreds, Tens and Ones
Estimated Time
35-40 minutes
Materials/ Resources needed
Paper, scale, pencil, marker, a pair of scissors
Prerequisites/Instructions, if any
Multimedia resources
Website interactives / links/ simulations
Process (How to do the activity)
- Above is a sheet with 10 vertical lines and 10 horizontal lines. Taken together, we can see 10 'cells' in each row and 10 'cells' in each column.
- Print 32 sheets of this '10 * 10' squares.
- Distribute into 8 groups of 4 children each.
- Each group will get 4 such sheets.
- The value of 4 squares will be 4x100 = 400
- Each group will cut the sheets such that
- They can cut 2 sheets along the solid (darker / vertical) lines; here each sheet (10*10 square) will have 10 such "strips". These are "tens", each strip has 10 cells. So each square has 10 “tens” (They can either *cut, or work without cutting – up to the children)
- They can cut the other two sheets along both solid (darker / vertical) and the less dark / horizontal lines
- Each one of those sheets will have 100 cells
Developmental points/questions
- Let the children make numbers and write them down
- Ask them what is the largest number each group can make? 400 is the answer – but check if children understand this.
II. Abstraction from here (1 period)
In the previous activity we gave 4 sheets to students to actually cut and play with. Now let us assume children have 9 such squares.
In each group, how many hundreds are possible ? – 9
In each group, how many tens are there ? – 9 x 10 = 90
In each group, how many ones are there ? – 90 x 10 = 900
1-9 ones are possible; 10 ones means one ten. Ten ones is the same as one ten
1-9 tens are possible; 10 tens means one hundred. Ten tens is the same as one hundred.
What happens when we have 10 hundreds? What is it the same as?
What is the importance of ten? We count in groups of tens
9+1= 10 = 10 x 1
99 + 1 = 100 = 10 x 10
999 + 1 = 1000 = 10 x 100
Greatest 1-digit number + 1 = Smallest 2-digit number
Greatest 2-digit number + 1 = Smallest 3-digit number
Greatest 3-digit number + 1 = Smallest 4-digit number
Following the pattern, we can expect that, on adding 1 to the greatest 4-digit number
(9999 – nine thousand nine hundred and ninety nine) we get the smallest 5-digit number
(9999 + 1 = 10,000 or ten thousand). Further we can expect that 10 x 1000 = 10,000 i.e.
9999 + 1 = 10,000 = 10 x 1000.
Do this only when children are confident – this is for advanced students
| Hundreds | Tens | Ones | Number | Comments |
|---|---|---|---|---|
| 3 | 8 | 3 | 383 | Watch if students are stating numbers are correct |
| 4 | 7 | 2 | Watch if students are stating numbers are correct | |
| 0 | 3 | 5 | Ask how many hundreds there are? They should say this number is less than hundred | |
| 1 | 10 | 5 | Do they say 205? What is the answer? | |
| 2 | 8 | 3 | Without forming the number can they say if number >200? Can they say if this is greater than number below? | |
| 2 | 7 | 5 | Without forming the number can they say if number >200? | |
| 10 | 7 | 3 | What is the answer here?Point out “regrouping”. This is important for addition/ subtraction | |
| 11 | 8 | 2 | What is the answer here? Think about how students are doing 10 hundreds plus 1 hundred. Point out “regrouping”. This is important for addition/ subtraction | |
| 1 | 7 | 4 | 3 | Without forming the number can they say if number >200? |
Evaluation (Questions for assessment of the child)
- Making numbers
Suppose we have 4 digits 7, 8, 3, 5. We want to make different 4-digit numbers using these digits such that no digits are repeated in each number. For example, you can make 7835 and 3578 but 7738 is not allowed because 7 is repeated and 5 is not used.
a. What is the greatest number you can make?
b. What is the smallest number?
c. Can you write down how you make the greatest number and the smallest number?
Use the given digits without repetition and make the greatest and smallest 4-digit numbers. Note that 0753 is a 3 digit number and is therefore not allowed.
- Now make the greatest and smallest 4-digit numbers by using any one digit twice.
Hint: Think about which digit you will use twice.
- Make the greatest/ smallest 4-digit numbers using any 4 different digits with conditions as given
Question Corner
Activity Keywords
To link back to the concept page