Similarity and Congruence

The Story of Mathematics

Philosophy of Mathematics

Teaching of Mathematics

Curriculum and Syllabus

Topics in School Mathematics

Textbooks

Question Bank

While creating a resource page, please click here for a resource creation checklist.

Concept Map

Error: Mind Map file 5a._Similar_and_Congruent_triangles.mm not found

Textbook

To add textbook links, please follow these instructions to: (Click to create the subpage)

Teaching Outlines

Concept #1 - Understanding similarity

Learning objectives

1. To show similar planar figures, discuss congruence and properties of congruent/ similar triangles

Notes for teachers

These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.

Activity No #1 Identifying similar shapes, similar triangles

Click to Comment

• Estimated Time - 80 minutes (40 +40)
• Materials/ Resources needed - Blackboard, Geogebra files + projector, Calculator
• Prerequisites/Instructions, if any
• Multimedia resources
• Website interactives/ links/ Geogebra Applets
• Process (How to do the activity)

1. Draw figures on the boards - planar figures and triangles
2. Draw pairs of figures on the board [ both similar and dissimilar]; they can identify overlap of congruent figures
3. Demonstrate using Geogebra files and discuss
4. As part of the procedure, the teacher can use the following points to evaluate the activity as well as evaluate student understanding

• Confusion between congruence and similarity
• When they give the theorem, if they cannot identify included side and angle
• When there is a wrong answer, identify what is the source of the confusion – sides, ratio and proportion
• Developmental Questions (What discussion questions)

1. Can you identify similar figures?
2. If the children know the names of the theorem, can they explain SSS, AAA, ASA?
3. What does a ratio of side mean? What is proportionality?
4. In the Geogebra files, when I change the sides/ proportion, the triangles change in size. But the proportion remains the same, angle remains the same
5. With calculator verify the proportion (this is very very useful for involving the whole class) they all can see the proportion remains constant though the size changes
6. Show the arithmetic behind the proportion

• Evaluation

1. Direct substitution in simple textbook problems
2. With a pencil and a ruler, how can you estimate the height of a pole

• Question Corner

Activity No # 2 Review of the concepts of similarity and congruence

Click to Comment

• Estimated Time - 30 minutes
• Materials/ Resources needed -Projector, Computer
• Prerequisites/Instructions, if any
• Multimedia resources

• Website interactives/ links/ Geogebra Applets
• Process (How to do the activity)
• Developmental Questions (What discussion questions)
• Evaluation (Questions for assessment of the child)
• Question Corner

Concept #

Notes for teachers

These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.

Activity No #

Click to Comment

• Estimated Time
• Materials/ Resources needed
• Prerequisites/Instructions, if any
• Multimedia resources
• Website interactives/ links/ Geogebra Applets
• Process (How to do the activity)
• Developmental Questions (What discussion questions)
• Evaluation (Questions for assessment of the child)
• Question Corner

Activity No #

Click to Comment

• Estimated Time
• Materials/ Resources needed
• Prerequisites/Instructions, if any
• Multimedia resources

Suchetha . S. S Asst. Teacher ( Mathematics ) GJC Thyamagondlu. Nelamangala Talluk Bangalore Rural District doing the activity below on a lesson on similar triangles using GeoGebra in the classroom

• Website interactives/ links/ Geogebra Applets
• Process (How to do the activity)
• Developmental Questions (What discussion questions)
• Evaluation (Questions for assessment of the child)
• Question Corner

Math Fun

Usage

Create a new page and type {{subst:Math-Content}} to use this template

Pythagorean Theorem

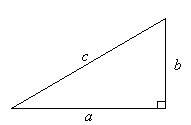
Pythagoras' Theorem was discovered by Pythagoras, a Greek mathematician and philosopher who lived between approximately 569 BC and 500 BC.

Pythagoras' Theorem states that:

In any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. That is:

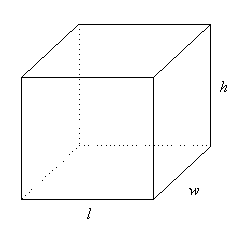
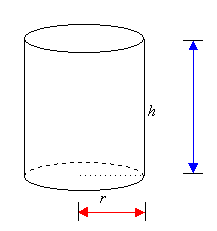
Pythagoras' Theorem in Three Dimensions

A three-dimensional object can be described by three measurements - length, width and height.

We can use Pythagoras' Theorem to find the length of the longest straw that will fit inside

the box or cylinder.

GeoGebra Contributions

1. The GeoGebra file below to understand Similar Triangles
   
   1. Similar Triangles Part 1 http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_1.html
   2. Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_1.ggb
   3. Similar Triangles Part 2 http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_2.html
   4. Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_2.ggb
   5. Similar Triangles Part 3 http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_3.html
   6. Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_3.ggb

1. The GeoGebra file below verifies the Thales theorem
   
   1. Thales Theorem http://www.karnatakaeducation.org.in/KOER/Maths/thales_theorem.html
   2. Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/thales_theorem.ggb
   3. See a video that proves this theorem http://www.youtube.com/watch?v=Y-6yYsuGLoc