Difference between revisions of "Triangles"
| Line 99: | Line 99: | ||
# They should have prior knowledge about angles formed when a transversal cuts a pair of parallel lines and the relationship between them. | # They should have prior knowledge about angles formed when a transversal cuts a pair of parallel lines and the relationship between them. | ||
* Multimedia resources:Laptop | * Multimedia resources:Laptop | ||
| − | * Website interactives/ links/ Geogebra Applets: | + | * Website interactives/ links/ Geogebra Applets: Geogebra file 1. |
| − | <ggb_applet width="1000" height=" | + | <ggb_applet width="1000" height="600" version="4.0" ggbBase64="UEsDBBQACAAIAHSHmkMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ2WVeVQS6BrGsRhDpERNyWUKCTU1NMdlKrdQXEDHJXXyuuUQUWriCS2XcglTEdQU3LdGtBKXcdArLmQ65eSCmjOlJjDaWBqlKJppwugM595z77nd+eP9Ped73vd9znfO98eX4+vtvh+sCwYAAPuxHpizCh1SVChIWUGzVhkfAFAuxGLQAYkCSXWMb0DgoXR2JOG9e93UyY8ZkUaVbeVVHCPVDo7sJ7G1v/83aRWy2nvezsNlZSB2Ge7Vvjkc/tinHJPvbx8pxqYPgam5TXtoN0GjsmJKQy74oaRbmOmqHapuzpPaW62KeDee1TgkbKVsLvde2gpVU0onrb0yBJyBAoBK/8U7TBx9iG/CvXinJThW2hSR8ojXgmiJCevcXtZMwrs8k8Td73Vb1eyqhVeOxOQwAmYLrZ8ZCafcV8UeiI6qH90JL4hCybAOV74xwYe0G618CDltXNs46Ggw59WeuWPbS5L3BHj9NudXuvN6g4wjydc370x32vF80uFhE5qkm8FvMf72xcfWCfjBndVlSVWoxRVNnfIXNmyJU/mkjO4AYsU+X+Ja1E35nI87Tp2frEbc2elbqTZfT3R+yxULq38zPlOQvVthhVr6ZUksOVeVYBUadxeABkCB/8Fnh8/wb60v/bS99nQvJd4AicSE6zkErohibDeSQoJD7PrE7cSPLIacSFmTip9f9wKrDWbVmnt8zIwqtycVNVdsZ4lIPSSv2I4UXiIqCJ43Njb/bsnsgrYFyWf00uJ48VptrSDGQSAQ6CckOToiamoQR93itZFWz7mkI2+f2V3J9iHUQ7a2pklNXLHEl//axkawjvNnah8Q3oJn6PlHcpHHZUHkuDTm5Pk8Gy+G3KmbVzfos1ZCWtSo/Mr1zWyvY3R21N7eYagWkhRSsOwDKaHR8DNxJ8IRj1LDVmajyKvVUZfhdPX6O/nox47F807cEe4TlfnOq1mJY6nBizdtcfYPblAHISHSyT1ZzfAmilPBR7YTNniF2H2tO5yeVdGOp4EnkhnY75hDoEM9FH26ahTsiWMRcoZPHGpp0v5qT9aPcI7ql2CWJ6ODoMvoh2ojiehOSlcGchySkigVgoDvUPcbth0UA2SkKPaM4dV4t+nUstd+fAAl/pseu7Gp1qBbagcxrsx7T6eEkHRklNcE37Oe84ut+Umi1/Sb69akl2Hlvz+J6Qz8h1yyxR8Y5hmYe7hc667yzrmGg4Yxqhba3yQHsj034DuBylBM3aYYzR7BJQQrWstKDCB0wNd7Nb/U7BLtMA6KvGVw1CPhAnwcxzogLQSilVHjVT8l+x5sOY/489uyYV2gzm2KfQRkYOaEqzJ1AWNengHPoP/hKEYXKGZb4YUfZF5QJLoA/XOe4AN+9vDkA0rDsZlDNCRofvdF+S5jxIUnD4VqGbfMs2VKaFGJ1TsVMgfZeh7odxVhMmr6yrxNBS1iPv7kKghyS1OhKNam9Okqy+dOKeJFuv4balkgFssahZaPweBUYcERnYgyuOmIFXNB9AhFgFG69rmfk+uZUmltvTlkU8MSiAt0enFx4bQJFvx1qOJe0M5+sr276YErelB0PHbUxJKgS+kyep+ocG/0A/38kk4GjgepzSqhQ/NZ+z0X3FIW0sEs1vu7vWcZDxm5irDHBKlO8z7s2S5barMLFKYx0G/5r9ijc5nJUIfGFsbBARRSDiWkR0Yz/6AmmRtTwZ5X8w8a/wDfq0541ZUyyTKsNVM8NJ5WY9GC2hrCAC1r6Mbr9ccv1PHBvyZy3LTd0gzSzKvzkSC8vXpTX5FN32iJaiARZWB8XG/1LAXz52EjnSThzwkL2W1mUqY346XPKTDoV4vb42k+5PXr9Lmn5YLJuvwi/YkSWONYsOhhwKUyCPtUpbAVfy+7Z6S4R7+KtrBmdXFsOUdDnZPfjIFmALeneA5KO8y+wsYRxmZNfd8NZrQWsZtgG1mburub1H/yVMLl0rKEgSF2NYdMXtJVuWvll7o7HkI/sSR7WerGjzvqhPcOA1pmaaXGRpIhelNGmYtP2uxtuvi5Ocka07Ddlp3YsMzTJD+mfcOxoK26641BeQ8afNsfNXly2U7fsVXXL6vDkF9EZ9yD2/qatTrv7OIm/Us42ErYpyvh91/ALg7nyUxRpPDGay+JNk12cI++10t6iNnW3I5NRGy0Q46sKF+2mxLiHKIZZvjPChOOdUqGTWpxnLwTVx2ooXWOTxNqzkhaKaqgeaogmA78IlN6YC8FAAcB/g9/d/7XPtMnPTL/PS9iztLkd8UfBcC6emN+cI6g/AVQSwcIUrT7SrUGAADKBgAAUEsDBBQACAAIAHSHmkMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAB0h5pDAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1ZW3PbNhZ+Tn8Fhg992YjClZdUTsf2TGczkzaZOt3Z6RtEQjJrimBJyJY7/VO5/I78ph4ApERatmPH3m5SjSUQxOE5ON+5Ep59v1mV6Fw1baGrg4CEOECqynReVMuDYG0WkyT4/vk3s6XSSzVvJFroZiXNQcAtZZEfBDjlUTrnarIgUTLhC6kmyZynk0ilCcOxEvM8DxDatMWzSv8kV6qtZaZOslO1ki91Jo0TfGpM/Ww6vbi4CHtRoW6W0+VyHm5aYADbrNqDoLt4BuxGD10wR04xJtP//vjSs58UVWtklakAWRXWxfNvnswuiirXF+iiyM0pKEwT0ONUFctTUCoWNEBTS1UDIrXKTHGuWnh2MHVKm1UdODJZ2fUn/gqVW30ClBfnRa4aAChklCQ4EQRHLKFpnIgA6aZQlemIcSd02rObnRfqwvO1V04kD5DRupxLyxL9+SeimGL01A7EDxSGKPJL2N/DzA/UD9wPwtNw/zj3pNzTcE/DWYDOi7aYl+ogWMiyBQyLatGA/bbz1lyWyu2nu7FTnzwlsF78AcQMg3oedLiP8VP7jeDLcaf3QEkykGqa9f2E4l5kRMTdRdIHKUq3akZsXyYVN6gZ3SLU630buL1MIgbQgij35757Etltal6V6OcPExjxv0XF2bQPlVkXHag9tbSd9xi1am28sBSJ1Lo9QQJiI4rBywUiKQwxRRANiAjEBUxJgiI7xojFsMARQwmydIQhFxwigR8eO2YREsDM3o0hJhEBQRwJhoiLKY4gkpCLS4hRyoBCCCTgISueUMuCRYhHMGMJ4rBHG5IxAUIGD8IcxFPECGL2YRIjGqHI8iPchnqU2K0DS4oijCJiGUJUQ0T7aAb6BDGrTdTBVVT12owgylZ5f2l0vbUFUEM+2qU9n59GWfHJrJRzVUKlOLGWROhcluBpgRO00JVBvRGpv7dsZH1aZO2JMgaeatFv8ly+lEZtfgDqtpftaDNdta8bbY51uV5VLUKZLvF2z7okg2u63TVM2GCBDxfEYCEaXMfXytWwgtatAvm6aXtymecvLMUuNQCSr6ry8qhR8qzWxViN2dQVnZlaZ2WRF7L6DzirlWJxQbsaFCe7GiSSpN+JbvKTyxZcGG1+VY2GbJNEIRt8wKqXfoXhyBbkNpM23hgbkTFITZc3LHWmUedbo8iN2um3bGwwDyYv2iNd7m45lY9lbdaN6xhAUmP1OKyWpXJu4YIZynF2NtebE+8PzPN6c1krm7bdDuZLBzWCdEAF5O9lN8796Gjs1rZU2NFgR4F7Byvy7TpJqaNw49yPjgo81m+tU5X0ahLciyla39sEXaj0Ccr6uy3u66owL/uJKbKznar2gZ/Wq7naes2YJ3ksnrPpFbeanammUmXnxWDMtV63PigHDp6rrFjB1C90kEhrrl9gA/5urpaN6jdeum7MA+ZW8dA/9247Vj80evWiOn8DvnBlA7Npv8tZmzVFbX0OzSHzn6mdV+VFK6Fw5MPnbNiB6pktEACPsdBAQK7NqW5cvwV5BEYbbaVaQXOFjHMv56FbmA9d22bxRHr+G6SybbXz6zuDwfK1ruacUpb1qbStXad0KS9VM4LB8ftR51fBAeydBhDWtbdtrZR3C79fuKiBnYumUV4CtFu0gQ2EaQrxDLEWCiD+w3ftvmu1utoYG6Vif/eKocB7PEyfAOzo6weMhGnsAJvwkCX/c8SO/wGI4dD2bxYyFqbsUSDL9GolqxxVrgN8rcvLpa6CXU8isY1OJIn1OSSpBdKjtDb9eg1PEU+TeRoJA1T8uZfWybjGQF5abwLPZ1wLDHQmZ/D61bqm3nSlyV38u8hz5brS6e2mHYA5tC0RzFnXhqsrVjvjkvsY92YPbNXSzrYbyT7hg/ff6D29cOdLcZj4dDUBD4KXz8GHOseaUOBOcHq1ON/dIOr3yj/S+opZrOqyyAqz9Z/S+vqLykD9VK6A7JfFM6Vq24+8qt40smrtMYenGZTbO4IvvxzwJzjkPB1+YuaMkYRR7NBnSZhEhPxjwJ9/QeDHIWcj8IUPhDiMhAOfpyFOY7KLCPEV2WGc0F3DfyWdH/lUfXhTOv/49va07VrJreWA2h2NyXLdIx6m8OoUJzSOOY4jHIlPJejbai/B+J7p+dVi0SpjTe0zHLneMfZeO+5uVNlkg0rbV/iy1Bc/q0WpNg71h5ioq7jH3kRH+yZ6dy8Tvds3UULhLTMlnFJGI94fBfz9JprY0LbRR786Ix2P2qLDfSO9v5eR3l81EglZilkswFIpTwUX/P9lpKjrFL60QFKbugExtqvuEVAbAw4FCwfBt7+vtfnOs2jXK1Q3ulaNuUR6gSQyTeEM4Kkc57F5LKtgzPezalh/bOLhdxXtc4uYO71rVVMsdidd/ugmCvoC05G2Rjbmte3+kQszFrJ42OQlvujFIWXD26M319uh/vihw/njW/Qv9PGd/XnvTyhv9fMPV/2chYQTkdJIMJGkccoexw3YyA2+LcEVjo4P/Mzu9e11e90zOvs8o/cx151x2fGzjV5sVD5Wfs+8SUjIsKOh3UkEJUPjYn5361rd+R6CR8eHAwTf3QlB/hhh84DO7y74Eci1dAgg6wEcBQ25J4BiD8Djw6MBgNeGyx6A4qtwQcJDgYcQkg7CUX65T4KxutPrghig65yxuwJU0QHa4frhTrjSh+D6CEdCd0IVA3777yokFGNY45tgnQ4PaN2/Prr/4z//C1BLBwj/J9rSAQgAAGQgAABQSwECFAAUAAgACAB0h5pDUrT7SrUGAADKBgAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZ1BLAQIUABQACAAIAHSHmkNFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAPkGAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAdIeaQ/8n2tIBCAAAZCAAAAwAAAAAAAAAAAAAAAAAVwcAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAwADAMIAAACSDwAAAAA=" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> |
* Process (How to do the activity): | * Process (How to do the activity): | ||
# The teacher can initially recaptulate about a triangle, its vertices, sides and angles. | # The teacher can initially recaptulate about a triangle, its vertices, sides and angles. | ||
Revision as of 17:15, 26 December 2013
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Error: Mind Map file Triangles .mm not found
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Useful websites
This is a reference website for types and classification off triangles
A good website for quick reference of all theorems in geometry. Suitable for both students and teachers.
Reference Books
Teaching Outlines
Concept #1 A triangle and its basic properties
Learning objectives
- A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments.
- It is the polygon with the least number of sides.
- A triangle can be defined as a polygon which has 3 sides, 3 angles and 3 vertices.
- The sum of any two sides is always greater than the third side.
- The angle opposite to longest side is the largest.
- The angles inside the triangle are its interior angles.
- The sum of all 3 interior angles in any triangle is always 180 degrees which is called the angle sum property of a triangle.
- The external angle of a triangle is always equal to the sum of its two opposite interior angles.
Notes for teachers
[These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.]
- A triangle PQR consists of all the points on the line segment PQ,QR and RP. The three line segments, PQ, QR and RP that form the triangle PQ, are called the sides of the triangle PQR.
- A triangle has three angles. In figure, the three angles are ∠PQR ∠QRP and ∠RPQ
- A triangle has six parts, namely, three sides,PQ QRand RP.Three angles ∠PQR ∠QRP and ∠RPQ. These are also known as the elements of a triangle.
- The point of intersection of the sides of a triangle is known as its vertex. In figure, the three vertices are P, Q and R. In a triangle, an angle is formed at the vertex. Since it has three vertices, so three angles are formed. The word triangle =tri + angle ‘tri’ means three. So, triangle means closed figure of straight lines having three angles.
Activity No # 1 Make your triangle
- Estimated Time - 40 minutes
- Materials/ Resources needed; Paper, pencil, and scale.
- Prerequisites/Instructions, if any:
- The students should know points and line segments.
- Multimedia resources
- Website interactives/ links/ Geogebra Applets
- Process (How to do the activity):
- Mark three non-collinear point P, Q and R on a paper.
- Join these points in all possible ways. The segments are PQ, QR and RP.
- A simple close curve formed by these three segments is called a triangle. It is named in one of the following ways.
- Triangle PQR or Triangle PRQ or Triangle QRP or Triangle RPQ or Triangle RQP .
- Developmental Questions (What discussion questions):
- What are plane figures ?
- What is a polygon ?
- How many points are needed to make a traingle ?
- Evaluation (Questions for assessment of the child):
- What are the intersecting points of a triangle called ?
- Can you draw a triangle with collinear points.
- Question Corner
- Name the elements of a triangle.
Activity No # 2. Angle sum property of a triangle
- Estimated Time: 40 minutes
- Materials/ Resources needed:Laptop, projector, geogebra file and a pointer.
- Prerequisites/Instructions, if any:
- The students should know a triangle and its elements.
- They should have prior knowledge about angles formed when a transversal cuts a pair of parallel lines and the relationship between them.
- Multimedia resources:Laptop
- Website interactives/ links/ Geogebra Applets: Geogebra file 1.
- Process (How to do the activity):
- The teacher can initially recaptulate about a triangle, its vertices, sides and angles.
- Show them the geogebra file.
- Let them read the angles and find its sum
- By moving the vertices she can reiterate that the sum of angles in any triangle is always 180 degrees.
- To demonstrate this she can show them the two parallel lines across the triangle .
- Identify the transversal.
- Let them identify the two pairs of alternate angles from the figure.
- Developmental Questions (What discussion questions):
- Identify the geometric figures you see in the geogebra file.
- Identify the parallel lines.
- Identify the triangle embedded between the two parallel lines.
- Identify the 3 interior angles of the triangle.
- Name the transversal ?
- Name the types of angles formed at the point of intersection when a pair of parallel lines are intersected by a transversal.
- What are the relationship between such angles.
- Identify the 2 pairs of alternate angles.
- Why are alternate interior angles equal ?
- What is the sum of angles formed at point A ?
- What can you say about the 3 interior angles of a triangle ?
- How can we determine the relationship between the alternate angles and the interior angles of the triangle .
- Evaluation (Questions for assessment of the child):
- Can we prove the angle sum property of triangle by any other method. Discuss.
- Question Corner:
- Try proving the theorem by drawing different triangles.
- Cut on the outline of triangle.
- Cut out 3 angles of a triangle and join 3 vertices next to each other.
- Repeat for different triangles. What do you infer?
Activity No # 3. External angle property of a triangle
- Estimated Time: 40 minutes
- Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any:
- The students should know a triangle and its basic elements.
- They should know interior and exterior angles of a triangle.
- They should know that sum of angles along a straight line is 180 degrees.
- Multimedia resources: Laptop
- Website interactives/ links/ Geogebra Applets:
This geogebra file was contributed by Mallikarjun Sudi of Yadgir.
- Process (How to do the activity):
- The teacher can move the 'explain slider' to show how the sum of opposite interior angles equals to external angle.
- Developmental Questions (What discussion questions):
- Identify the interior angles of this triangle.
- What are exterior angles ?
- Name the exterior angle from the figure.
- Name its two opposite interior angles.
- What is the measure of the marked exterior angle?
- What is the sum of two opposite interior angles?
- What can you infer ?
- Evaluation :
- Reason out as to why external angle is equal to sum of opposite interior angles of a triangle.
- Question Corner:
- Try to prove external angle theorem using linear pair concept and angle sum property of a triangle
Concept # 2 - Types of triangles
Learning objectives
- Triangles are classified into different types depending on their measures of sides and angles.
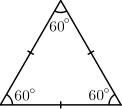
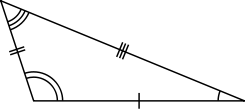
- Based on sides they can be scalene if all sides are of different lengths, isosceles if two sides are equal and equilateral if all 3 sides are of same length.
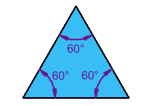
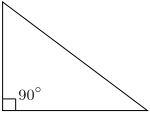
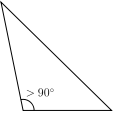
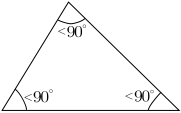
- Based on angles, the triangles are classified as Acute angled triangle if all of its angles are acute angled, Obtuse angled if any one of its angles is obtuse, right angled if one of its angles is 90 degrees and as equiangular if all its 3 angles are equal to 60 degrees.
- An equilateral triangle is equiangular as well.
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activity No # 1. Types of triangles
- Estimated Time: 40 minutes.
- Materials/ Resources needed:Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any:
- The students should have prior knowledge of plane figures, triangles, vertex, angles and sides of triangles.
- They should know the types of angles and measuring angles.
- They should know that triangles are classified depending on their side lengths as well as angle measurements.
- Multimedia resources:Laptop
- Website interactives/ links/ Geogebra Applets:
- Process (How to do the activity):
- Begin a discussion like : “ All triangles have ....” .
- Show them different triangles by moving the vertices.
- Let students discuss what they noticed about these different triangles (e.g. different side lengths).
- The teacher will lead the discussion with the questions: “What did you notice about the length of the sides?”, “Do they all have the same length?”
- Through this discussion help the students develop vocabulary and definitions for the following: equilateral triangle, isosceles triangle, and scalene triangle.
- Developmental Questions (What discussion questions): # What did you notice about the sides of the triangles ?
- How many different side lengths can a triangle have? (hint: all 3 sides equal or 2 sides equal all different )
- What type of a triangle is this ? Why ?
- Evaluation (Questions for assessment of the child):
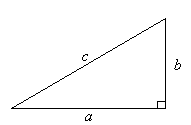
- Identify the different types of triangles from the following images:
|
|
|
|
|
|
- Question Corner:
- What does the term side of a triangle mean ?
- If it is an equilateral triangle, then it has ___ sides that are of the same length.
- If it is an isosceles triangle, then it has ___ sides that are of the same length.
- If it is a scalene triangle, then it has ___ sides that are of the same length
- Can a scalene triangle also be a right-angled triangle ? If yes can you draw one ?
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ Geogebra Applets
- Process (How to do the activity)
- Developmental Questions (What discussion questions)
- Evaluation (Questions for assessment of the child)
- Question Corner
Concept #3 - Properties and Theorems:
Learning objectives
- If two sides of a triangle are congruent, then the angles opposite the sides are congruent. This is called isosceles triangle theorem.
- Conversely if two angles of a triangle are congruent then the sides opposite the congruent angles are congruent.
- An equilateral triangle is also equiangular.
- The pythogoras theorem which states that the square of the hypotenuse of a right angled triangle is equal to the sum of the squares of the other two sides.
- Thales theorem states that a line drawn parallel to any side of the triangle divides the other two sides proportionally.
Notes for teachers
- The GeoGebra file below verifies the Thales theorem
- Discovered by Pythagoras, a Greek mathematician and philosopher who lived between approximately 569 BC and 500 BC. Pythagoras' Theorem states that: In any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. That is:
Pythagoras' Theorem in Three Dimensions
A three-dimensional object can be described by three measurements - length, width and height.
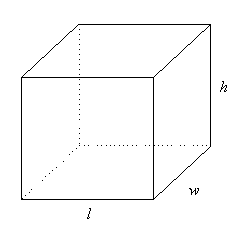
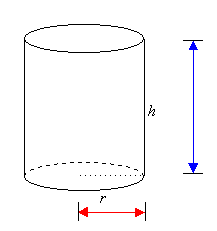 We can use Pythagoras' Theorem to find the length of the longest straw that will fit inside the box or cylinder.
We can use Pythagoras' Theorem to find the length of the longest straw that will fit inside the box or cylinder.
Activity No # 1. Thales theorem
- Estimated Time:40 minutes
- Materials/ Resources needed:Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any:
- The students should have knowledge about a triangle and its elements.
- They should parallel lines.
- They should have knowledge about ratio and proportionality.
- They should know the angle relationships when a transversal cuts parallel lines.
- Multimedia resources:Laptop
- Website interactives/ links/ Geogebra Applets:
- Process (How to do the activity):
- The teacher can reiterate a triangle and its elements.
- Show them the geogebra file and explain the thales theorm or the basic proportionality theorm which states that a line segment drawn parallel to one side of a triangle divides the other two sides proportionally.
- She can prove the theorm for different measurements by moving the vertices of the triangle and also by moving D, to change the position of parallel line.
- Also she can use the same file to explain the converse theorm which states that a line segment that divides any two sides of a triangle proportionally is parallel to the third side.
- While proving converse theorm, she can show that since the corresponding angles <ADE = <ABC and <AED = <ACB, the line DE that divides AB and AC proportionally is infact parallel to BC.
- Developmental Questions (What discussion questions);
- Name the sides of the triangle.
- What is a parallel line ?
- What does the basic proportonality theorm state ?
- Name the parallel line from file ?
- DE is parallel to which side of the triangle ?
- What are the lengths of AD and DB ?
- What are the measures of AE and EC ?
- What is the ratio AD/DB ? and that of AE/EC ?
- Are the two proportioanal ?
- What are the areas of triangles ADE and ABC ?
- What is their ratio ?
- Is AD/DB = AE/EC = (area ADE)/(area ABC).
- Recall thales theorm.
Part B:
- What does the converse of thales theorm state ?
- Name the line that divides the two sides AB and AC sides of the triangle proportionally.
- How can we prove that DE is parallel to BC ?
- Recall transversal and parallel lines concepts /
- Identify the transversal ?
- Identify the corresponding angles.
- What are the measures of corresponding angles ?
- Are <ADE and <ABc equal ?
- Also are <AED = <ACB ?
- What does equality of correspondng angles indicate ?
- What is your inference ?
- Evaluation (Questions for assessment of the child):
- Recall the basic proportionality theorm and its converse.
- Question Corner:
- Formulate any three of your own questions which can be solved using the above theorems.
Activity No # 2. Pythogoras theorem
- Estimated Time:
- Materials/ Resources needed:
- Prerequisites/Instructions, if any:
- Multimedia resources:
- Website interactives/ links/ Geogebra Applets:
- Process (How to do the activity):
- Developmental Questions (What discussion questions):
- Evaluation (Questions for assessment of the child):
- Question Corner:
Activity No # 3. Isosceles triangle theorem
- Estimated Time:
- Materials/ Resources needed:
- Prerequisites/Instructions, if any:
- Multimedia resources:
- Website interactives/ links/ Geogebra Applets:
- Process (How to do the activity):
- Developmental Questions (What discussion questions):
- Evaluation (Questions for assessment of the child):
- Question Corner:
Hints for difficult problems
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template