Difference between revisions of "Cyclic quadrilateral"
Jump to navigation
Jump to search
| Line 174: | Line 174: | ||
*Multimedia resources: Laptop | *Multimedia resources: Laptop | ||
*Website interactives/ links/ / Geogebra Applets: | *Website interactives/ links/ / Geogebra Applets: | ||
| + | This geogebra file was done by ITfC-Edu-Team. | ||
<ggb_applet width="1280" height="600" version="4.0" ggbBase64="UEsDBBQACAAIACGDkkMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZwH1FArriVBORw0KGgoAAAANSUhEUgAAAMgAAABgCAYAAABYFz0dAAAUvElEQVR42u1dC1BVR5pmZqoyW1tbMZWHUbc0m0l0Ro1JfK5GR1jji0hinNKoIYZBCaLgQlAUUYGUqPgImgQfoyLi6qoJig9KEVnxMWo0Ib6igM/41pgdTazRWZV8e79D+tL3cM7lXLhc7oXuqlPn0f13/326//4f/Xe3H6Rw+fJluBpu375dq+k9BaPwqh94ubsufvLLzZs3XUbm7t27tZreUzAKr/qBl7vr4kAgp0+fdhmZGzdu1Gp6T8EovOoHXu6uiwOBnDt3zmVkbt26VavpPQWj8KofeLm7LkrEUngpEcuqiKU4iMJLcRClgyi8lA5iXQehaZeiFbnHsWPHtGd+I7HIcXw3ijt58qQWL+L4zmdeTCfiRB4XL140jRNwzEMuW+SpL1vOw1146cs2q7creMlly3jp622GlyvtweeSkhLL9baCl9E/McLLWXtUFy/2SavtIeLOnj1ruT1kvIzaw7d1kGHDgF/9CnjwACgr05G+X/nlahl6GH0+0rMhXiJef1c6iDLzepxl/va3sA0XwCuvAP37l38LCCgnGtGxxTvDCy84dlyp8z5inD5en65Vq4r3bt1Q9vTTjgQg4mU4XkzHIGA6dSq/RFrbdzRuXP7+2GNA06bl33v2NCU0JWJ5SMTyaSX9nXfKO/9TT8HGNysIRO6c4p3hd7+reH7yyYrn1q3L85Hj9R1dpOnaFfj1r4EePRyJR8SLd5FOTiNg9AQi5yWnt93Lmjd3mUCUkq7MvI7B3986jElHU6KMErGUmVfhpTiIMvMqvJQOUks6iJpJV3gpEUsRiMJLEUj1COSksAS5EK5cuVKr6T0Fo/CqH3i5uy4OBKIWTCm8fB0vd9dFiVg+gJcLUyBKxIIy81YKnFD3RryqC0NOPmxYCFJSUjFx4kQkJydj6tSpSE1Nxbp166rMQ5l53WjmJXshBTERHcP4zG80fclxfDeKo2mY8SKO8hyfeTGdiBN5fPfdd6ZxAo55yGWzDJH/qVOnkJGRgY6dAvEvT7XROlBCQgKSkpKwevVqez7VxUtftlm99XjJcXL++rJlvOT8+ZyWlobo6GjMmjUL/9yoBUZ9MFXDS+TPfIqKijRCmTBhAhYuXKh905d95swZy/WuCi+zfyLjZVZvd+BVXFxsuT1E3Pnz5y23h4yXvmw++4SIxUqx84tR9MSJE+g+2B9/6NYGSXOStDT379/HV199pcUz3a5du3yG/W/atAnx8fG4cOGC9h6VFIWwaWHwH+GP2z/edsppCLdy5Uo8fPhQiVi1LWJ5o5JeUFCAMWPG4MiRI/ZvqVmpCIkLwcX/vYge7/bQRgB9WLp0qUYoVtltXSiQbJiYmBitjnJ8h7c64Ortq5jxyQwMnDgQD8seOs2T/4b5cLRVSnotKuneNJPOEZGyN0dXGabkagk6BJZ3IF5pO9JsSqyfwwgqymHF2XHIcdxdj5rCXL9+HREREZVGr+DIYGTkZ9jr1z+4P/yG+sEvzA+37t5C7rFcRKyKwM8//2z4v0hsaia9lmbSvYWDiJHVaERs/3Z7rNq5yt6Bco7kIHBsIObNm2daDjnJvn37vGZ0oyhFHUJPHOSEXYd3xZLdS7CwcCHG/fc4tBjfAh+Ef6CJkN1Tu6Pf/H5OOQrFLXJPxUHqqZmXI2FUVFQlUYShsLAQGZkZWHNoDabkTEHCxgSs/2q9FrdkyRIcPHjQtByOrkLGr0v5mPUi59BzPAYSDQmh+Hoxztw8oxECyxC6BsOde3eqLIP/QhbblA7iJh3EG0QsjvZ6nUJYFtiBnAVyHVFZfTnskIw36pieZP+sgxGhkvhpwjUrg/HkDlbx4oAgOLASsdwkYtX1PAj1jby8PEMYdqyqyqJcTwIzK4cjMa1cdWVvZyfPzMw05ZpVlbFgwQLNUmcFr6oGhNpsR1+D8YkFU2xIMw6RnZ2tEY+VwHS5ubmm5XBkNZI5PcHKZQ4nh+XLl5t2fH165lFVBxAwtG5Z5TpKxPJyJT09Pd3QXMvOwE7hSqC8zp0tzLiMXqH3hDJI7kHi1cPwXegXVsoQBgxnnEGGYd5WOoxS0r1cBxGikdGoW1paWun7ntN7MD13uqaop+Sm4JuL3zh0opEjRzolIE/LuqJMPUxKSopGtK6UQd2CcFZgOOiRQykdxA06SF1xEHIOo0ak0sqR18Gi9Y+7iFwTiTdD3kRRaRG+2PIFzt86j08KPsHUTVPtJtCdO3eadgxaefR1tVIPvdOg1brTMkXRTg/DehtxMzlsPLQRkzdO1gaCTd9ssiR26vESZSsOUkMOUlc6CDuJXq5mBxZcRYYZtHAQ1hasRVp6GmbPn22fD+F14OwBTNs0zQ5DhdxIbOM3uq5YqceIER8iMHCE9lxUVL260+RKQtfDCLOuUbj8t8sIXxWOjD0Vk4brD6/HhM8n4MGjB3buY2Sp0uNF8dWq3qJ0EB2BeIOzIh0O9c5x48aNs6cRToHfXvgWY1aOQfHFYpy+chpHTx/FiXMntGd+4/v4teNx62/lMBRdRo8ereWhx4tlVuWsSMKNiEi04TK5Rs6KLEv/v7Zt24Zly5ZVco5j3KWblxC6PBQHTh7AoROHtLpxJp1Xck6y/dlvpB9GR4zWrI/OnALp4EhlXTkr1tBZsa7MvHoRQD/pJ2B2ntqJeTvmOXAN/bVg5wJc+OGCHYY/2EiMkcukOCbjxXkKTubJ/l81qbtcljDBmpl1GSZvmIzia8VafTgAyPULmBuAtPw0fP3d13ajg976p8dLcNNqmzr9lJm3TkUsuQOxc+oVUAHDDhK1Jgrnbp1D/Ip4tBrUCk16NEGn8E5Y+D8LtfhJ2ZNw7//uOZQjE9zaQ2uRuDkR/rH+yPs2r1IZFL1YvpnoU526y/UjjDOzLsPE7Il2giB3HDx0MJJnJmvvJddL7PUUgXlxjsQZXmZGEDOYqHfiEDUoWolY3qCkiw7EkTV8TDgScxId/I0Iww67fft2NPFvgmYBzdA7ojc2Fm5EYFAgUpel4tW3XkXT15vitYTXDMuJHBeJP6b8EXkn8rQONn7aeGz8ZiPGfz5eK4vr8Tmqy5zLXXWXCYSiiTOzLkPcF3HaIJC+MQWpo7vh+RZPYWjCUAdOMvGLiQ4wJDqh5zj7x1XWZbdN8V8wofyulHTv2LRBNN7sebMRnBqM/Wf2a8ooZUMqmFxExFGdDod5x/OQfzLf3lGGjxhufx6bORYxH8VoHXD+/PkOXGDkopFo2a8lFu9ebCcQ3rcd34Yhk4YgNjbW5ZHHat3lzjmtb19cdya62RorJbwzVg/rjM0f/gmFuatw8dZFDI0fisavNda4ZcGpAs1iZ2RKpsjl7B+bhR82ZAAfxwBfF9ZKu3szjOVNG+rSirX7r7vR68+9kLEuA9ETojF41GDEpsRqDS7DlP1chtTtqcj+Ohull0vR741+2n1x4WJtXkQEKqbsFLwybI2/4q8r8JdVf8Hz7z2PL49/iXmL5mFJ3hJ0HNAR2/O31yorF53zzJo1SA0NZYU5c+hAFKDJlmKSTZk+sn8Lth7bahexZM4xP2s+nvN/Dh1COlSaLOSAQN1JGxEpwn36KdCxY8X16JHje8cOwNaVwGfxuLdvm7JieSuBkFP8U6PmeH/0+8jZnqONmOz4SZuTDGG4FmLd4XUYv3484j6P0+6yPiHDsBMNmTwEEdER+GjWR/h9r99jcMJgBMUEIWhEkJ29eoJAJvTsiR9KSoDvv7eN1h9T4bETBS5dsrG5isnNpXuWakRNArFbrWxXo/9sVP48yA9P/PsT+Oyzzxw45cnSk/hzhz8AW7aUl2O7zhw4gF3TbYPH3LnA3/9uI5SH5YRBUar0iDLz+oI377NNXkGz1s8hcWGifbSkS3t1ytDDCKX3iK0zBIcG4zeNfoMl/7WkRvVwBYYOmMN7BiA7Lg4/LVrkOIoz8N6rVzknkRZCFRQXYOzKsRr+vDhZSE55/8F9h8FFLEUmscd+Hosp40OQ/PZ/2Alk2cyZuHbsGLB3NxD9rsYxBGG4ux19EcYnvHmpZHLlX1hSGHq92wsbDm9A1sEst5j6nmnxjEYgYZFhePbFZ5E8I9mj5kSO8I0fa4vZQUG4s2ePveMiKcltZVAU/XDSh+g3oh8KvyxEeOBryJ6VoJUzJ3qcjY1FAiG9bRT1ba2bRpWZ183sLDKyYr0GQ+7+XLzU5yX7Utmastllucvw4ksvoue7PRE7KdbQhFvbrJxzCVHdu6PYpofYCYQ6gpvK4GrDzP2Z2FG0A/HT4hEVE4UBLzRBYt8+uBFk0zXWrPCYWFJvRay6Xg9CEyutVkJ3oPLOOQyrZfhJM1oCZqZNvOjSpQtC0kKwa98uU/fv2h6paIJdv349Jtq4yL6EBMpdwI4dbimDOknRxSK7nvJEqB8mBfkhsMWTePGZf8M/DNxtFAepBgfxhhWFdFCkI55MNPTM1Vfi+p3rWL5vOZK3JCNmXQwOnjuozYiLcPz4cQQEBNhnmeVlq3Ul6xIXmhTTp0zBap6O5eYyjh/Nx4JhzyDnT6+i35uvIHRyqN2hcdo0z7ZjvdFBrPgWOfOB4cSXK75YFOOq8r+hwsnN4UQc52c4F0LCYbrSS6UYnTUae4/v1Vwxjp4/ivT8dAxfPBxXbl7RuFCbNm20vbGYB93lQ0ND7eU5w8uVjeOE/5bVjeNoek5MTNTicnJytA3vrPyvqtrj++Lj+GHmOOQHv45uga0xK2uWFs/tkqz6PMntaMUXywivqnyxOEi56osl+5lZ9cW6du2aS75YAi+f2jiOlh9ODlLUEjDkLjSZhq0Iw+mbpyv5YWXuzkTLji01jiNg6IZhtINIXcnHNEaIZcX0EzNbZWipjEtncP2jCGwfFoDFc2bZTdZsWKMthZQOUkMdxNuOPyBls3NzVlxMitFX6/1R72PE3BHaxnH2WfSUsXi6xdPI35WvpaOjIYmJOkxt1KMmMPKGChy16OIiNnLYenSrZtKN3xCviY9RK6Ow78y+SoRxNmYINg57HWuzMh0mDPlM4nC2CMvT7ejtMD5//MHevXs1QiFHobJLK9S06dPQ54M+KLlcglZdW6Fr765a3pS5OS/AvXpdKcuTfkJikzfBSfhOnIdPH47somwHrni49DAW7V6E95a/h9tFhTgyqj82B/fFnp2VFXzhhcxlC97YjmrBVC2zTBIGFx+RUNjBgkcG49l/bYeXO3XQ3qm7CC9ZXxAZ6DlML1zBAVLmpCAwKtDOGYVV6tXBfpjbyQ8hHfzQPqadtsOifmdF6mf8B7JI6q3tqMy8HjTbxcYa6xe+YrakqEXuKCx3a7LXoPvQ7jh38xx2pE9Gpn8TzHm7LQqKKlxpOOchAjkm9ZhCybdLHX+gTrmtd3ixg9MMTe6YvjwdLzVugre6tMGps6cc0pFDMC25BdPLhNGQ/pfHzLy+JGKZhR9/rD8iA8VI6ibt27+O6OgZmilYeCXzIgFRzHS2oEuJWA3o+ANvUNTqCoaOAep/qX2xlIhlErp0Uf9L7YulRkSFl69wkKp0ED+D7S2E/Hbv3j3DeD3s9/Ri/SW8/PLL9ucpU6Zo1gRxdBrTCxi9jCi+y2ms4CrwNEpnJIfqcVKyfgPXQWQzr+h8+uvOnYrzKegcKMyTjRo10uKbN29uTzNw4EDtG/cpErCPP/44ysrKHDpn7969sWLFCjRr1kx7b9u2rb08PrOTsiy+M0/xLC5+E+WKd5G3eBY4CTyZh8hHwDGI56ZNm9oU5fZOib4hm1PVKbdeesqtVec4Xzvllq4hb7zxhjaYyHEkULP2kOP4TO5stEEb4/R48Zt+4ziRzqw9mL+AM9o4jnGEZTp1yq0SGdwGI3NDBpkbyuKkGVcW8eSO5M5Xr1514LhyvvoynZUlpASxjECWEliGGT4CjwZl5pV/mqw7yAoO01Bu512W22XYqhQoI5HGCIbphD4hw4iG1uNVVVn6MvQwZnjJ/6ImCuFPP/2kdTbelZLuA2beSK6D/aVjGI1WeiWZcVlZWZouIZ/nwdFGhu3fv79dtxAjkBjZ9GmZRoxu+jh5xBQjnNAteBd10cOZjcDEyxkesk4knoVoI3AUd4G3qyZFvX+VMosrM68aERVe9cfMq3QQhVeDNvOqmXTvwsvq3JJ+bkeUYTbnYxTE2Yf6OR8zGLUvlkUFWtiQnf18M+XaV2zhnoQxsxo506GELibiRDu6MufTrl07hzYUeckbYXjj/6rttncqYjlT1IVyTfZUXeW6c+fOduSMFFQlMii8Grw3b/fu3ZXSCXO3GWfmaiMTszBxu8qllZJugUC8bdMGT8LUNV56dx4h4jA9xRzxrp/zMRK7OPssxKuG1o7urouyYim8lIjl7ccfqAYvD494foeOO4j0ctynv+zpq+cQYttWRSAeOOX27NmzCAoK0napY5xwZJOd4+Li4nDo0CFtl0DhrCY7ggnnNeWsWLWzYnh4OPz9/dGyZUsHZ0LiFRYWpsX17dvXHidfoj3EVR2nQHXKbTVOuR01apShgsjnzMxM7f4xD4IxSSP2ffJ1U5+nYGQuoU9vFNfQ/1edmnmNnOecLZhSIpbnRKyqlO+5c+c6XUwm51NdsazBL5giYQwaNAg//rJliMzC5VV/agGQe2A459SnTx+0bt3agQiYXsRt3rzZIU7vJi/mkmbMmGFqFWN48OBBJauY4iAWCETvaiKLWNRJjMyMYpre6qSfcjW54ZKIJdK7ImIpb14P7Isli1hmI5ZQ3MW7lUk/JWLVXMRS/8tLzLzkBHplWyYOfpcJxAoXUQRy16mIpRejmF7EDRgwQP2vuiQQZ968Vr06q+IiSsRSIpbPilhG3rx6m7ueWJSSrvBqMEq60Uy6fjmrFSuK0kEUXvVSxPLF4w8UXgovj3EQtaJQ4aV0EB2BeOMpt3rfH6unyboDr9o85baq02Sre8qtO06TVafcWvDFUruaKLx8HS9310WJWAovJWKpfbEUXoqDuIGDqAVTCi9fx8vddVFmXoVXvcLL3XVROojCS+kg9f2UW4WXwssjIpZS0hVeSklXIpbCS4lY1ROxFAdReCkOonQQhZfSQaqngygRS+GlRCzH8P/foBOtFRGtNgAAAABJRU5ErkJgglBLBwiSJOlW+hQAAPUUAABQSwMEFAAIAAgAIYOSQwAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAAIACGDkkMAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3rcuO2Ff6dPgVGncm005jGHWBip+PsJbtJWme6206nfzoUCcmMJVFLUr7s9KHapPfLnz7APlMPAFISRUk2vWuv7K3bLSUAJIjznct3cFEPfn4xHqEzkxdpNjnskQD3kJnEWZJOhoe9WTnY072ff/6jg6HJhqafR2iQ5eOoPOxx2zJNDnvKEBwKTfbiKDR7HA+SPS0itYcpw5qbmCSy30Pookg/nWS/jMammEaxeRGfmHH0TRZHpev4pCynn+7vn5+fB3VXQZYP94fDfnBRJD0ErzkpDnvVh0/hcY2bzplrTjEm+7/9xTf+8XvppCijSWx6yA5hln7+o48OztNJkp2j8zQpT2DAVMM4Tkw6PIFBKUF7aN+2moJEpiYu0zNTwL1LX92gy/G055pFE1v/kf+ERvPx9FCSnqWJyQ97OCCKaCV6KMtTMymrFqTqab9+xsFZas79w+wn1w/voTLLRv3IPgf94Q+IYorRJ/ZC/IXCRUpfhX0ZZv5C/YX7i/BtuL+d+6bct+G+DWc9dJYWaX9kDnuDaFSA4NLJIAfQ5t+L8nJk3PtUBYsxk09gTEX6GhozDFL1koZyjD+x/yT847ZivzlIstRrmc86dlp3SajS1++TvtVIWd0ppWvGScWGccotnfqBX2ugYqlP6Mr91/1r9ci2DXO1R//97TqU/E6GeLBf28pBZR6oOLFtK/UpzbiwBsNCJEKr9wQJMA6pQM0FIiFcFEVgDogIxAV8JRpJe1WIKajgiCGNbDvCkLMOoeF/uHIPk0jAw2ypAqNEBDriSDBEnFFxBKaEnGGCkVIGLYRAAm6y3RNqH8Ek4hK+MY04vKO1SUWgIYMb4Tt0TxEjiNmbiUJUImmfR7i1dantq8MjKZIYSWIfCGYNJu3NGdprxOxoZCWudDKdlZWIKqnH46QWV5lN58XQHDzSwtt5D9Vwhh8djKK+GUGAeGGhROgsGlmTcD0NskmJ5hbpy4Z5ND1J4+KFKUu4q0DfRWfRN1FpLp5C66Lu27WNs0nxbZ6Vj7LRbDwpEIqzEa5fFD6Tpc90MZhsxJYq+HKFWKqQS5/V2n4zqEGzwkD/WV7UzaMkeW5bLHwDiPJ4Mrr8IjfR6TRLm8M42Hex5sDM4lGapNHkN6CtthcrF7QIPdZh1aFHElW/SZYnLy4L0GF08TuTZ9BS84BjoqQWMtTYhpJLX0NDGmAhBWdMKU01g6oijqz1cRwICDtSspBSxhX4rMsNVcL3bM7mCEUXZjHYYZ7OdcV+fl58kY2SebUb/qNoWs5yRxqgo9yO6WgyHBmnIs6yISLHp/3s4oXXDeaf9fJyCt+wf4H+0IkdgW+gAkYyrK59f3Vt7JvNW2HXBrsWuFa2NJnXk5C6Fu7a91fXCrTXv1o1UlKPkuC6m7RwHg33mnbjdN/G99kkLb+pv5RpfLoYqr3hl7Nx38w1qPlM8q6eebC/omIHpyafmFGl0YDlLJsV3kCXlD0xcTqGr76iEklk4fo1vIAvTcwwN/WLjxwh8wJztXhZV1vF7lFP82z8fHL2EnRh5QUO9uu3PCjiPJ1alUN9CAOnZqFVSVpEEEWS5fusCcLQYxstQDylFQ0Y56w8yXJHucCnwNVa3siMgWqh0qmX09C5mI8cc7PyRFn/O3Br89Dn6xeAQfVaVXNKGY2mJ5Fld9WgR9GlyRticM87HgwKU6KLw94eAXO/hLvZUvUvsmRVdgCNGyB4gKljjwD+1BivN35A8GEK/TlzazgxgKOwfeEg5K4z+NBDrz2x98TWysLaYMNt+9IVIEG7vBivEOgXdyrQKyV2E3nRQHtwmBPcLQvsUVtgTU9waypI3SBBEW9ZniKgtNI//W7kGWfjcTRJ0MRRyUdpHo9Mb8FtImwNG0XEqiOKqBWyF+CsrOvj3xP/1OpZLZTAv6TxHATbfLtiLw19E0745nq9iFElsKdTSBILl7eUVch0H56lSWIcdfYhPB2ayRm8KZAXyLlxldFfYt8/el2XXICg9lzRJamKXpMllEAD8vQCHdXtj+pWRyBaFRCiIL8URGpLH8B0jljVwxGQrz0W4JAQSQkjMoTcU0G5sB4wkFJSRrHEMgTWMmceryZ+pIWPd5ZtpgPAYqsSfOuMqqkDFcYN3B9vR71pm49v5MwI9XTFXW9unqH3Qbfu7lhAJMEMCCWTWmItXb+gDxJAE1hqRcOQSiDw7950X5ihLd9ku6vgRdvBK6qn1fBE79VkFxK2JuAjMFlEFEKICBd/6i3sfMVg0vF0lMZpORffyKL/fFICXTSOL7VZ4KkxU0u/jycv82hS2Ik932aJXXbC8NEmDPvdMOzvDobEGwYNWIWhDgh4rYeLYWWHj1sYJt0wTHYEQwKZbsOleaOkwE9WHOBrBzinnOJQSMKUVpo9MHQfe3Tb1Mh0Q9fsCLpAKLhowMsqeLHQITANIhlhIfHGKwJoRYC3cBKGGm68R+huoyxP7n/+RYAZ+gSMB/jdsI5tEnv63qYAPNOq5/puT6BhoOoJAHXr4vzyvYkTe3MXd6efQJJDfVcZ7RPvr5/6jPbLltsedMlnB//PZtdms4RD2MfcrqxKooVQq9ksoY70UaEUI6HQapHOCvquE9hBC+RnXdLXZ+8xffXGSMJbN0YecCaAplENYV4DdJWn40DkhIQ6piXDRN5Z9jq301Xsht141XBHeBULQNGX/3wsAYUPWaNcVLwZnCLw5UX5QyPOTz3AbQ980g3gkx0BeB7ONiFKVABcubVads9h/NLD+KwFY9oNxnRHYASDZHrV57n8R4mGg5zPXoQklIRSianWVD80fJ95fJ+08P2uG77f7Qq+LJCEMEBXcshtZah0PSG1FmDBAmqVgRNOpViz2n1v8HWbB9Y74SeeDbeN+M2ftqPslqXnGEJrez+8z6wSPwkIiJOHgkqqQKSsEsXNEhuC24pArqkIb4FblMdLHKdmXaNRdv4rMxiZCyfYt0HhSe1DN+Qkb77vhML3bRSYFiEFxq251WTB7haFpfSSVbNJ9w6jLxt5Y9sdvvmhE0Y/tDEC9yMVIUoQLpnSN4Oo3uQjiMPIXh6UqTyrWaODoZ0dvPlzJxj+3IYBgjkGP0UhMRVCYPqhO6xHxgakK1Pq4y4p9fGNUmq7E3boL31/ucH0lvc/WycLlzj9mmkKx/DF3S3jViH6uCXx024E7PRmBGybQ7k5CcOBpnj5j1Qkm+MVcYOUZQAsXPgSCST7oS0QHm9KoUbdEB7tCMV2q/JLDFvPFwi1XR0UWDEgI7JOi2UQAt6CAe7AtNn9RXcLwT7eSLD/0ile/WU1XtGAQbwKQwyy45pr+aGHqy2k4XgjafhrJxD+ugoCC0JKsZYAgWQEpMg/PBTMxTSHbuw0dD1Gc1GCW4eKw97Hr2ZZ+dmjyxjsEb2aRUmejiIww2gEb2iy3IwL9Clq//n7XF9NSOzDe82e3oYuv7X3G6QXJmlKpzq5UZg8HSxOOfit+rJX+6jq/qKM8tItXiC/eVbKUBGmIXUG6w59eBSBAGsXIZZCcXCkbJmEXHdl8fkDWNqW9VIsCe5uRaLKAJ+33Me4W5gevxMi9m4mw2ggdKVaWDQmrZ1YGRSHy+sW92l/x9Vx4Xlj3mVNTv+3TnHhb2tyei44JBBcyBDTUIu7TuqXM59qvYmsVY1dCxy0EThIgF6eGJRNp1mRlgY5wRcoG6AIxeuCSpSDns2mU99LlF92CSX0vfLotZFkJTzYSWwmsSKKK86Z0kzOVxMFlhzSJaGAkGDJN4aItWJnDbF75KyVwRv1L22oBsnGKCrdxxieBHJOC5Rks77TmQqaeYs0j2fjgcnNJDbXB4DdBwAEo/Y4PgH3SIk9JOgXESTnUoXAB4k1+s0Req34+Rrxt4QNwP/3j9cXJr8XwqRLtIb6Pft7dskcpIyxUlpw1tzE1nHCat0hhq+6TFl9dbMDRjees9q6laB1FMRTodWDIHd80uCrloQn3ZjRZEcmMPZwoFqydDMYRKwI3s1gBKC9SoOWEi41FvOzYPePJa3H96tNe5yn3fCd7gi+dvZxPbxUa4imUjOswsp578mAYAIBlYBKAMAhubforuPAc9vdcMLvzd87ceC/tyeoOA0J/McdpxdUXUWBtyrB/ZwbuTYKG89ZvvlHJxT+0c5ELB8JRSil1iGV7MplrQ8ShkcNYzhqw/DPTjD8sz1RqAULrSkw4OiQcV85Ufghw/B4Iwz/6gTDv9Ys8lIZWluQCmPBrp6vfYAwrM9ARCMDubh+miF2Ps0A2qyXlxyrg/t2h9Lyn+6WssmGwC6vLzC58wKjgV6zRmsP3zZKO+a4qiGw/vUFpnZeYJCwNla1q62j0JdsFHcR2dHH0TQrPmsILbme0OpbbzLleKdqtqJQqvrZENpUP9VNz3TTk6FDRJNP0KW99j/+McFQ9DP31c+n2BKaQBHto8NFUf9nCTQBF9FlykXvvKa6Y7ma6VArDdLnIfb7YvZ4QBWHQmV//woUVYhuUg8bUqfBkwvIZVIYn58XTAtkXs3sql+G0klVtTKte305hzsvZ4IDIHxCANGQXEldnavZg1QzXCreMre1bU7q6/u/lCfd0T9/vvju9lRVh7a/bjHLV1f9ns3qlMar9/yLNo21PMkaB7dF5Uc1aRzcrlZMcWDpLxUh0Szk6oHtu/m6nrJyKUT79zPe/LtTCvHvdgohKRivtHs+Qq7Fldt133EGsVjYq9f11m9p3LX8wh4vXgoQ0w4bPPDOe3sRiAaTYfXEfJPfXG8ZY51Wf9HQ6vYvirzqotSv2joNsUqF4Ba4DkPC5JXHBG5NqfdYdZbufqxWk+Y+p+OVder2ajSg4+ilHUGUo2mU5m4127UPXNXHo/KzGLinvUboJy9Pxoj8tFUzrdkp+kn1rG/hWYt20/oJHQzt/Ua0a9IqJdzEDdMCTEqIesXQ7iAVnDKFpf0h1m7klTR3HcQdZPZ+9wysiAdIvOYsxBpMmAK9rA9zSxvqGRi5xkATbu6GKvp0tDG4/qdTcP3PmuAKWWAolNbSrgrLK3e13p4j8pol7sfsHWnu3+hi9Lu/54IElHKsbbJqf5VIKlb/HKY7l6kkodL+iP/GVGp/+cdu7ff6/xbh8/8BUEsHCDrvY4X6DgAAs2EAAFBLAQIUABQACAAIACGDkkOSJOlW+hQAAPUUAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV90aHVtYm5haWwucG5nUEsBAhQAFAAIAAgAIYOSQ0XM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAPhUAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAhg5JDOu9jhfoOAACzYQAADAAAAAAAAAAAAAAAAACcFQAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAwgAAANAkAAAAAA==" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> | <ggb_applet width="1280" height="600" version="4.0" ggbBase64="UEsDBBQACAAIACGDkkMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZwH1FArriVBORw0KGgoAAAANSUhEUgAAAMgAAABgCAYAAABYFz0dAAAUvElEQVR42u1dC1BVR5pmZqoyW1tbMZWHUbc0m0l0Ro1JfK5GR1jji0hinNKoIYZBCaLgQlAUUYGUqPgImgQfoyLi6qoJig9KEVnxMWo0Ib6igM/41pgdTazRWZV8e79D+tL3cM7lXLhc7oXuqlPn0f13/326//4f/Xe3H6Rw+fJluBpu375dq+k9BaPwqh94ubsufvLLzZs3XUbm7t27tZreUzAKr/qBl7vr4kAgp0+fdhmZGzdu1Gp6T8EovOoHXu6uiwOBnDt3zmVkbt26VavpPQWj8KofeLm7LkrEUngpEcuqiKU4iMJLcRClgyi8lA5iXQehaZeiFbnHsWPHtGd+I7HIcXw3ijt58qQWL+L4zmdeTCfiRB4XL140jRNwzEMuW+SpL1vOw1146cs2q7creMlly3jp622GlyvtweeSkhLL9baCl9E/McLLWXtUFy/2SavtIeLOnj1ruT1kvIzaw7d1kGHDgF/9CnjwACgr05G+X/nlahl6GH0+0rMhXiJef1c6iDLzepxl/va3sA0XwCuvAP37l38LCCgnGtGxxTvDCy84dlyp8z5inD5en65Vq4r3bt1Q9vTTjgQg4mU4XkzHIGA6dSq/RFrbdzRuXP7+2GNA06bl33v2NCU0JWJ5SMTyaSX9nXfKO/9TT8HGNysIRO6c4p3hd7+reH7yyYrn1q3L85Hj9R1dpOnaFfj1r4EePRyJR8SLd5FOTiNg9AQi5yWnt93Lmjd3mUCUkq7MvI7B3986jElHU6KMErGUmVfhpTiIMvMqvJQOUks6iJpJV3gpEUsRiMJLEUj1COSksAS5EK5cuVKr6T0Fo/CqH3i5uy4OBKIWTCm8fB0vd9dFiVg+gJcLUyBKxIIy81YKnFD3RryqC0NOPmxYCFJSUjFx4kQkJydj6tSpSE1Nxbp166rMQ5l53WjmJXshBTERHcP4zG80fclxfDeKo2mY8SKO8hyfeTGdiBN5fPfdd6ZxAo55yGWzDJH/qVOnkJGRgY6dAvEvT7XROlBCQgKSkpKwevVqez7VxUtftlm99XjJcXL++rJlvOT8+ZyWlobo6GjMmjUL/9yoBUZ9MFXDS+TPfIqKijRCmTBhAhYuXKh905d95swZy/WuCi+zfyLjZVZvd+BVXFxsuT1E3Pnz5y23h4yXvmw++4SIxUqx84tR9MSJE+g+2B9/6NYGSXOStDT379/HV199pcUz3a5du3yG/W/atAnx8fG4cOGC9h6VFIWwaWHwH+GP2z/edsppCLdy5Uo8fPhQiVi1LWJ5o5JeUFCAMWPG4MiRI/ZvqVmpCIkLwcX/vYge7/bQRgB9WLp0qUYoVtltXSiQbJiYmBitjnJ8h7c64Ortq5jxyQwMnDgQD8seOs2T/4b5cLRVSnotKuneNJPOEZGyN0dXGabkagk6BJZ3IF5pO9JsSqyfwwgqymHF2XHIcdxdj5rCXL9+HREREZVGr+DIYGTkZ9jr1z+4P/yG+sEvzA+37t5C7rFcRKyKwM8//2z4v0hsaia9lmbSvYWDiJHVaERs/3Z7rNq5yt6Bco7kIHBsIObNm2daDjnJvn37vGZ0oyhFHUJPHOSEXYd3xZLdS7CwcCHG/fc4tBjfAh+Ef6CJkN1Tu6Pf/H5OOQrFLXJPxUHqqZmXI2FUVFQlUYShsLAQGZkZWHNoDabkTEHCxgSs/2q9FrdkyRIcPHjQtByOrkLGr0v5mPUi59BzPAYSDQmh+Hoxztw8oxECyxC6BsOde3eqLIP/QhbblA7iJh3EG0QsjvZ6nUJYFtiBnAVyHVFZfTnskIw36pieZP+sgxGhkvhpwjUrg/HkDlbx4oAgOLASsdwkYtX1PAj1jby8PEMYdqyqyqJcTwIzK4cjMa1cdWVvZyfPzMw05ZpVlbFgwQLNUmcFr6oGhNpsR1+D8YkFU2xIMw6RnZ2tEY+VwHS5ubmm5XBkNZI5PcHKZQ4nh+XLl5t2fH165lFVBxAwtG5Z5TpKxPJyJT09Pd3QXMvOwE7hSqC8zp0tzLiMXqH3hDJI7kHi1cPwXegXVsoQBgxnnEGGYd5WOoxS0r1cBxGikdGoW1paWun7ntN7MD13uqaop+Sm4JuL3zh0opEjRzolIE/LuqJMPUxKSopGtK6UQd2CcFZgOOiRQykdxA06SF1xEHIOo0ak0sqR18Gi9Y+7iFwTiTdD3kRRaRG+2PIFzt86j08KPsHUTVPtJtCdO3eadgxaefR1tVIPvdOg1brTMkXRTg/DehtxMzlsPLQRkzdO1gaCTd9ssiR26vESZSsOUkMOUlc6CDuJXq5mBxZcRYYZtHAQ1hasRVp6GmbPn22fD+F14OwBTNs0zQ5DhdxIbOM3uq5YqceIER8iMHCE9lxUVL260+RKQtfDCLOuUbj8t8sIXxWOjD0Vk4brD6/HhM8n4MGjB3buY2Sp0uNF8dWq3qJ0EB2BeIOzIh0O9c5x48aNs6cRToHfXvgWY1aOQfHFYpy+chpHTx/FiXMntGd+4/v4teNx62/lMBRdRo8ereWhx4tlVuWsSMKNiEi04TK5Rs6KLEv/v7Zt24Zly5ZVco5j3KWblxC6PBQHTh7AoROHtLpxJp1Xck6y/dlvpB9GR4zWrI/OnALp4EhlXTkr1tBZsa7MvHoRQD/pJ2B2ntqJeTvmOXAN/bVg5wJc+OGCHYY/2EiMkcukOCbjxXkKTubJ/l81qbtcljDBmpl1GSZvmIzia8VafTgAyPULmBuAtPw0fP3d13ajg976p8dLcNNqmzr9lJm3TkUsuQOxc+oVUAHDDhK1Jgrnbp1D/Ip4tBrUCk16NEGn8E5Y+D8LtfhJ2ZNw7//uOZQjE9zaQ2uRuDkR/rH+yPs2r1IZFL1YvpnoU526y/UjjDOzLsPE7Il2giB3HDx0MJJnJmvvJddL7PUUgXlxjsQZXmZGEDOYqHfiEDUoWolY3qCkiw7EkTV8TDgScxId/I0Iww67fft2NPFvgmYBzdA7ojc2Fm5EYFAgUpel4tW3XkXT15vitYTXDMuJHBeJP6b8EXkn8rQONn7aeGz8ZiPGfz5eK4vr8Tmqy5zLXXWXCYSiiTOzLkPcF3HaIJC+MQWpo7vh+RZPYWjCUAdOMvGLiQ4wJDqh5zj7x1XWZbdN8V8wofyulHTv2LRBNN7sebMRnBqM/Wf2a8ooZUMqmFxExFGdDod5x/OQfzLf3lGGjxhufx6bORYxH8VoHXD+/PkOXGDkopFo2a8lFu9ebCcQ3rcd34Yhk4YgNjbW5ZHHat3lzjmtb19cdya62RorJbwzVg/rjM0f/gmFuatw8dZFDI0fisavNda4ZcGpAs1iZ2RKpsjl7B+bhR82ZAAfxwBfF9ZKu3szjOVNG+rSirX7r7vR68+9kLEuA9ETojF41GDEpsRqDS7DlP1chtTtqcj+Ohull0vR741+2n1x4WJtXkQEKqbsFLwybI2/4q8r8JdVf8Hz7z2PL49/iXmL5mFJ3hJ0HNAR2/O31yorF53zzJo1SA0NZYU5c+hAFKDJlmKSTZk+sn8Lth7bahexZM4xP2s+nvN/Dh1COlSaLOSAQN1JGxEpwn36KdCxY8X16JHje8cOwNaVwGfxuLdvm7JieSuBkFP8U6PmeH/0+8jZnqONmOz4SZuTDGG4FmLd4XUYv3484j6P0+6yPiHDsBMNmTwEEdER+GjWR/h9r99jcMJgBMUEIWhEkJ29eoJAJvTsiR9KSoDvv7eN1h9T4bETBS5dsrG5isnNpXuWakRNArFbrWxXo/9sVP48yA9P/PsT+Oyzzxw45cnSk/hzhz8AW7aUl2O7zhw4gF3TbYPH3LnA3/9uI5SH5YRBUar0iDLz+oI377NNXkGz1s8hcWGifbSkS3t1ytDDCKX3iK0zBIcG4zeNfoMl/7WkRvVwBYYOmMN7BiA7Lg4/LVrkOIoz8N6rVzknkRZCFRQXYOzKsRr+vDhZSE55/8F9h8FFLEUmscd+Hosp40OQ/PZ/2Alk2cyZuHbsGLB3NxD9rsYxBGG4ux19EcYnvHmpZHLlX1hSGHq92wsbDm9A1sEst5j6nmnxjEYgYZFhePbFZ5E8I9mj5kSO8I0fa4vZQUG4s2ePveMiKcltZVAU/XDSh+g3oh8KvyxEeOBryJ6VoJUzJ3qcjY1FAiG9bRT1ba2bRpWZ183sLDKyYr0GQ+7+XLzU5yX7Utmastllucvw4ksvoue7PRE7KdbQhFvbrJxzCVHdu6PYpofYCYQ6gpvK4GrDzP2Z2FG0A/HT4hEVE4UBLzRBYt8+uBFk0zXWrPCYWFJvRay6Xg9CEyutVkJ3oPLOOQyrZfhJM1oCZqZNvOjSpQtC0kKwa98uU/fv2h6paIJdv349Jtq4yL6EBMpdwI4dbimDOknRxSK7nvJEqB8mBfkhsMWTePGZf8M/DNxtFAepBgfxhhWFdFCkI55MNPTM1Vfi+p3rWL5vOZK3JCNmXQwOnjuozYiLcPz4cQQEBNhnmeVlq3Ul6xIXmhTTp0zBap6O5eYyjh/Nx4JhzyDnT6+i35uvIHRyqN2hcdo0z7ZjvdFBrPgWOfOB4cSXK75YFOOq8r+hwsnN4UQc52c4F0LCYbrSS6UYnTUae4/v1Vwxjp4/ivT8dAxfPBxXbl7RuFCbNm20vbGYB93lQ0ND7eU5w8uVjeOE/5bVjeNoek5MTNTicnJytA3vrPyvqtrj++Lj+GHmOOQHv45uga0xK2uWFs/tkqz6PMntaMUXywivqnyxOEi56osl+5lZ9cW6du2aS75YAi+f2jiOlh9ODlLUEjDkLjSZhq0Iw+mbpyv5YWXuzkTLji01jiNg6IZhtINIXcnHNEaIZcX0EzNbZWipjEtncP2jCGwfFoDFc2bZTdZsWKMthZQOUkMdxNuOPyBls3NzVlxMitFX6/1R72PE3BHaxnH2WfSUsXi6xdPI35WvpaOjIYmJOkxt1KMmMPKGChy16OIiNnLYenSrZtKN3xCviY9RK6Ow78y+SoRxNmYINg57HWuzMh0mDPlM4nC2CMvT7ejtMD5//MHevXs1QiFHobJLK9S06dPQ54M+KLlcglZdW6Fr765a3pS5OS/AvXpdKcuTfkJikzfBSfhOnIdPH47somwHrni49DAW7V6E95a/h9tFhTgyqj82B/fFnp2VFXzhhcxlC97YjmrBVC2zTBIGFx+RUNjBgkcG49l/bYeXO3XQ3qm7CC9ZXxAZ6DlML1zBAVLmpCAwKtDOGYVV6tXBfpjbyQ8hHfzQPqadtsOifmdF6mf8B7JI6q3tqMy8HjTbxcYa6xe+YrakqEXuKCx3a7LXoPvQ7jh38xx2pE9Gpn8TzHm7LQqKKlxpOOchAjkm9ZhCybdLHX+gTrmtd3ixg9MMTe6YvjwdLzVugre6tMGps6cc0pFDMC25BdPLhNGQ/pfHzLy+JGKZhR9/rD8iA8VI6ibt27+O6OgZmilYeCXzIgFRzHS2oEuJWA3o+ANvUNTqCoaOAep/qX2xlIhlErp0Uf9L7YulRkSFl69wkKp0ED+D7S2E/Hbv3j3DeD3s9/Ri/SW8/PLL9ucpU6Zo1gRxdBrTCxi9jCi+y2ms4CrwNEpnJIfqcVKyfgPXQWQzr+h8+uvOnYrzKegcKMyTjRo10uKbN29uTzNw4EDtG/cpErCPP/44ysrKHDpn7969sWLFCjRr1kx7b9u2rb08PrOTsiy+M0/xLC5+E+WKd5G3eBY4CTyZh8hHwDGI56ZNm9oU5fZOib4hm1PVKbdeesqtVec4Xzvllq4hb7zxhjaYyHEkULP2kOP4TO5stEEb4/R48Zt+4ziRzqw9mL+AM9o4jnGEZTp1yq0SGdwGI3NDBpkbyuKkGVcW8eSO5M5Xr1514LhyvvoynZUlpASxjECWEliGGT4CjwZl5pV/mqw7yAoO01Bu512W22XYqhQoI5HGCIbphD4hw4iG1uNVVVn6MvQwZnjJ/6ImCuFPP/2kdTbelZLuA2beSK6D/aVjGI1WeiWZcVlZWZouIZ/nwdFGhu3fv79dtxAjkBjZ9GmZRoxu+jh5xBQjnNAteBd10cOZjcDEyxkesk4knoVoI3AUd4G3qyZFvX+VMosrM68aERVe9cfMq3QQhVeDNvOqmXTvwsvq3JJ+bkeUYTbnYxTE2Yf6OR8zGLUvlkUFWtiQnf18M+XaV2zhnoQxsxo506GELibiRDu6MufTrl07hzYUeckbYXjj/6rttncqYjlT1IVyTfZUXeW6c+fOduSMFFQlMii8Grw3b/fu3ZXSCXO3GWfmaiMTszBxu8qllZJugUC8bdMGT8LUNV56dx4h4jA9xRzxrp/zMRK7OPssxKuG1o7urouyYim8lIjl7ccfqAYvD494foeOO4j0ctynv+zpq+cQYttWRSAeOOX27NmzCAoK0napY5xwZJOd4+Li4nDo0CFtl0DhrCY7ggnnNeWsWLWzYnh4OPz9/dGyZUsHZ0LiFRYWpsX17dvXHidfoj3EVR2nQHXKbTVOuR01apShgsjnzMxM7f4xD4IxSSP2ffJ1U5+nYGQuoU9vFNfQ/1edmnmNnOecLZhSIpbnRKyqlO+5c+c6XUwm51NdsazBL5giYQwaNAg//rJliMzC5VV/agGQe2A459SnTx+0bt3agQiYXsRt3rzZIU7vJi/mkmbMmGFqFWN48OBBJauY4iAWCETvaiKLWNRJjMyMYpre6qSfcjW54ZKIJdK7ImIpb14P7Isli1hmI5ZQ3MW7lUk/JWLVXMRS/8tLzLzkBHplWyYOfpcJxAoXUQRy16mIpRejmF7EDRgwQP2vuiQQZ968Vr06q+IiSsRSIpbPilhG3rx6m7ueWJSSrvBqMEq60Uy6fjmrFSuK0kEUXvVSxPLF4w8UXgovj3EQtaJQ4aV0EB2BeOMpt3rfH6unyboDr9o85baq02Sre8qtO06TVafcWvDFUruaKLx8HS9310WJWAovJWKpfbEUXoqDuIGDqAVTCi9fx8vddVFmXoVXvcLL3XVROojCS+kg9f2UW4WXwssjIpZS0hVeSklXIpbCS4lY1ROxFAdReCkOonQQhZfSQaqngygRS+GlRCzH8P/foBOtFRGtNgAAAABJRU5ErkJgglBLBwiSJOlW+hQAAPUUAABQSwMEFAAIAAgAIYOSQwAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK7lAgBQSwcIRczeXRoAAAAYAAAAUEsDBBQACAAIACGDkkMAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3rcuO2Ff6dPgVGncm005jGHWBip+PsJbtJWme6206nfzoUCcmMJVFLUr7s9KHapPfLnz7APlMPAFISRUk2vWuv7K3bLSUAJIjznct3cFEPfn4xHqEzkxdpNjnskQD3kJnEWZJOhoe9WTnY072ff/6jg6HJhqafR2iQ5eOoPOxx2zJNDnvKEBwKTfbiKDR7HA+SPS0itYcpw5qbmCSy30Pookg/nWS/jMammEaxeRGfmHH0TRZHpev4pCynn+7vn5+fB3VXQZYP94fDfnBRJD0ErzkpDnvVh0/hcY2bzplrTjEm+7/9xTf+8XvppCijSWx6yA5hln7+o48OztNJkp2j8zQpT2DAVMM4Tkw6PIFBKUF7aN+2moJEpiYu0zNTwL1LX92gy/G055pFE1v/kf+ERvPx9FCSnqWJyQ97OCCKaCV6KMtTMymrFqTqab9+xsFZas79w+wn1w/voTLLRv3IPgf94Q+IYorRJ/ZC/IXCRUpfhX0ZZv5C/YX7i/BtuL+d+6bct+G+DWc9dJYWaX9kDnuDaFSA4NLJIAfQ5t+L8nJk3PtUBYsxk09gTEX6GhozDFL1koZyjD+x/yT847ZivzlIstRrmc86dlp3SajS1++TvtVIWd0ppWvGScWGccotnfqBX2ugYqlP6Mr91/1r9ci2DXO1R//97TqU/E6GeLBf28pBZR6oOLFtK/UpzbiwBsNCJEKr9wQJMA6pQM0FIiFcFEVgDogIxAV8JRpJe1WIKajgiCGNbDvCkLMOoeF/uHIPk0jAw2ypAqNEBDriSDBEnFFxBKaEnGGCkVIGLYRAAm6y3RNqH8Ek4hK+MY04vKO1SUWgIYMb4Tt0TxEjiNmbiUJUImmfR7i1dantq8MjKZIYSWIfCGYNJu3NGdprxOxoZCWudDKdlZWIKqnH46QWV5lN58XQHDzSwtt5D9Vwhh8djKK+GUGAeGGhROgsGlmTcD0NskmJ5hbpy4Z5ND1J4+KFKUu4q0DfRWfRN1FpLp5C66Lu27WNs0nxbZ6Vj7LRbDwpEIqzEa5fFD6Tpc90MZhsxJYq+HKFWKqQS5/V2n4zqEGzwkD/WV7UzaMkeW5bLHwDiPJ4Mrr8IjfR6TRLm8M42Hex5sDM4lGapNHkN6CtthcrF7QIPdZh1aFHElW/SZYnLy4L0GF08TuTZ9BS84BjoqQWMtTYhpJLX0NDGmAhBWdMKU01g6oijqz1cRwICDtSspBSxhX4rMsNVcL3bM7mCEUXZjHYYZ7OdcV+fl58kY2SebUb/qNoWs5yRxqgo9yO6WgyHBmnIs6yISLHp/3s4oXXDeaf9fJyCt+wf4H+0IkdgW+gAkYyrK59f3Vt7JvNW2HXBrsWuFa2NJnXk5C6Fu7a91fXCrTXv1o1UlKPkuC6m7RwHg33mnbjdN/G99kkLb+pv5RpfLoYqr3hl7Nx38w1qPlM8q6eebC/omIHpyafmFGl0YDlLJsV3kCXlD0xcTqGr76iEklk4fo1vIAvTcwwN/WLjxwh8wJztXhZV1vF7lFP82z8fHL2EnRh5QUO9uu3PCjiPJ1alUN9CAOnZqFVSVpEEEWS5fusCcLQYxstQDylFQ0Y56w8yXJHucCnwNVa3siMgWqh0qmX09C5mI8cc7PyRFn/O3Br89Dn6xeAQfVaVXNKGY2mJ5Fld9WgR9GlyRticM87HgwKU6KLw94eAXO/hLvZUvUvsmRVdgCNGyB4gKljjwD+1BivN35A8GEK/TlzazgxgKOwfeEg5K4z+NBDrz2x98TWysLaYMNt+9IVIEG7vBivEOgXdyrQKyV2E3nRQHtwmBPcLQvsUVtgTU9waypI3SBBEW9ZniKgtNI//W7kGWfjcTRJ0MRRyUdpHo9Mb8FtImwNG0XEqiOKqBWyF+CsrOvj3xP/1OpZLZTAv6TxHATbfLtiLw19E0745nq9iFElsKdTSBILl7eUVch0H56lSWIcdfYhPB2ayRm8KZAXyLlxldFfYt8/el2XXICg9lzRJamKXpMllEAD8vQCHdXtj+pWRyBaFRCiIL8URGpLH8B0jljVwxGQrz0W4JAQSQkjMoTcU0G5sB4wkFJSRrHEMgTWMmceryZ+pIWPd5ZtpgPAYqsSfOuMqqkDFcYN3B9vR71pm49v5MwI9XTFXW9unqH3Qbfu7lhAJMEMCCWTWmItXb+gDxJAE1hqRcOQSiDw7950X5ihLd9ku6vgRdvBK6qn1fBE79VkFxK2JuAjMFlEFEKICBd/6i3sfMVg0vF0lMZpORffyKL/fFICXTSOL7VZ4KkxU0u/jycv82hS2Ik932aJXXbC8NEmDPvdMOzvDobEGwYNWIWhDgh4rYeLYWWHj1sYJt0wTHYEQwKZbsOleaOkwE9WHOBrBzinnOJQSMKUVpo9MHQfe3Tb1Mh0Q9fsCLpAKLhowMsqeLHQITANIhlhIfHGKwJoRYC3cBKGGm68R+huoyxP7n/+RYAZ+gSMB/jdsI5tEnv63qYAPNOq5/puT6BhoOoJAHXr4vzyvYkTe3MXd6efQJJDfVcZ7RPvr5/6jPbLltsedMlnB//PZtdms4RD2MfcrqxKooVQq9ksoY70UaEUI6HQapHOCvquE9hBC+RnXdLXZ+8xffXGSMJbN0YecCaAplENYV4DdJWn40DkhIQ6piXDRN5Z9jq301Xsht141XBHeBULQNGX/3wsAYUPWaNcVLwZnCLw5UX5QyPOTz3AbQ980g3gkx0BeB7ONiFKVABcubVads9h/NLD+KwFY9oNxnRHYASDZHrV57n8R4mGg5zPXoQklIRSianWVD80fJ95fJ+08P2uG77f7Qq+LJCEMEBXcshtZah0PSG1FmDBAmqVgRNOpViz2n1v8HWbB9Y74SeeDbeN+M2ftqPslqXnGEJrez+8z6wSPwkIiJOHgkqqQKSsEsXNEhuC24pArqkIb4FblMdLHKdmXaNRdv4rMxiZCyfYt0HhSe1DN+Qkb77vhML3bRSYFiEFxq251WTB7haFpfSSVbNJ9w6jLxt5Y9sdvvmhE0Y/tDEC9yMVIUoQLpnSN4Oo3uQjiMPIXh6UqTyrWaODoZ0dvPlzJxj+3IYBgjkGP0UhMRVCYPqhO6xHxgakK1Pq4y4p9fGNUmq7E3boL31/ucH0lvc/WycLlzj9mmkKx/DF3S3jViH6uCXx024E7PRmBGybQ7k5CcOBpnj5j1Qkm+MVcYOUZQAsXPgSCST7oS0QHm9KoUbdEB7tCMV2q/JLDFvPFwi1XR0UWDEgI7JOi2UQAt6CAe7AtNn9RXcLwT7eSLD/0ile/WU1XtGAQbwKQwyy45pr+aGHqy2k4XgjafhrJxD+ugoCC0JKsZYAgWQEpMg/PBTMxTSHbuw0dD1Gc1GCW4eKw97Hr2ZZ+dmjyxjsEb2aRUmejiIww2gEb2iy3IwL9Clq//n7XF9NSOzDe82e3oYuv7X3G6QXJmlKpzq5UZg8HSxOOfit+rJX+6jq/qKM8tItXiC/eVbKUBGmIXUG6w59eBSBAGsXIZZCcXCkbJmEXHdl8fkDWNqW9VIsCe5uRaLKAJ+33Me4W5gevxMi9m4mw2ggdKVaWDQmrZ1YGRSHy+sW92l/x9Vx4Xlj3mVNTv+3TnHhb2tyei44JBBcyBDTUIu7TuqXM59qvYmsVY1dCxy0EThIgF6eGJRNp1mRlgY5wRcoG6AIxeuCSpSDns2mU99LlF92CSX0vfLotZFkJTzYSWwmsSKKK86Z0kzOVxMFlhzSJaGAkGDJN4aItWJnDbF75KyVwRv1L22oBsnGKCrdxxieBHJOC5Rks77TmQqaeYs0j2fjgcnNJDbXB4DdBwAEo/Y4PgH3SIk9JOgXESTnUoXAB4k1+s0Req34+Rrxt4QNwP/3j9cXJr8XwqRLtIb6Pft7dskcpIyxUlpw1tzE1nHCat0hhq+6TFl9dbMDRjees9q6laB1FMRTodWDIHd80uCrloQn3ZjRZEcmMPZwoFqydDMYRKwI3s1gBKC9SoOWEi41FvOzYPePJa3H96tNe5yn3fCd7gi+dvZxPbxUa4imUjOswsp578mAYAIBlYBKAMAhubforuPAc9vdcMLvzd87ceC/tyeoOA0J/McdpxdUXUWBtyrB/ZwbuTYKG89ZvvlHJxT+0c5ELB8JRSil1iGV7MplrQ8ShkcNYzhqw/DPTjD8sz1RqAULrSkw4OiQcV85Ufghw/B4Iwz/6gTDv9Ys8lIZWluQCmPBrp6vfYAwrM9ARCMDubh+miF2Ps0A2qyXlxyrg/t2h9Lyn+6WssmGwC6vLzC58wKjgV6zRmsP3zZKO+a4qiGw/vUFpnZeYJCwNla1q62j0JdsFHcR2dHH0TQrPmsILbme0OpbbzLleKdqtqJQqvrZENpUP9VNz3TTk6FDRJNP0KW99j/+McFQ9DP31c+n2BKaQBHto8NFUf9nCTQBF9FlykXvvKa6Y7ma6VArDdLnIfb7YvZ4QBWHQmV//woUVYhuUg8bUqfBkwvIZVIYn58XTAtkXs3sql+G0klVtTKte305hzsvZ4IDIHxCANGQXEldnavZg1QzXCreMre1bU7q6/u/lCfd0T9/vvju9lRVh7a/bjHLV1f9ns3qlMar9/yLNo21PMkaB7dF5Uc1aRzcrlZMcWDpLxUh0Szk6oHtu/m6nrJyKUT79zPe/LtTCvHvdgohKRivtHs+Qq7Fldt133EGsVjYq9f11m9p3LX8wh4vXgoQ0w4bPPDOe3sRiAaTYfXEfJPfXG8ZY51Wf9HQ6vYvirzqotSv2joNsUqF4Ba4DkPC5JXHBG5NqfdYdZbufqxWk+Y+p+OVder2ajSg4+ilHUGUo2mU5m4127UPXNXHo/KzGLinvUboJy9Pxoj8tFUzrdkp+kn1rG/hWYt20/oJHQzt/Ua0a9IqJdzEDdMCTEqIesXQ7iAVnDKFpf0h1m7klTR3HcQdZPZ+9wysiAdIvOYsxBpMmAK9rA9zSxvqGRi5xkATbu6GKvp0tDG4/qdTcP3PmuAKWWAolNbSrgrLK3e13p4j8pol7sfsHWnu3+hi9Lu/54IElHKsbbJqf5VIKlb/HKY7l6kkodL+iP/GVGp/+cdu7ff6/xbh8/8BUEsHCDrvY4X6DgAAs2EAAFBLAQIUABQACAAIACGDkkOSJOlW+hQAAPUUAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV90aHVtYm5haWwucG5nUEsBAhQAFAAIAAgAIYOSQ0XM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAPhUAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAhg5JDOu9jhfoOAACzYQAADAAAAAAAAAAAAAAAAACcFQAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAwgAAANAkAAAAAA==" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> | ||
*Process: | *Process: | ||
Revision as of 13:41, 6 January 2014
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Error: Mind Map file Cyclic_quadrilateral.mm not found
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Useful websites
Reference Books
Teaching Outlines
Concept # 1. Cyclic quadrilateral and its properties
Learning objectives
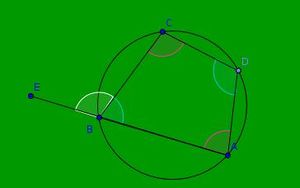
- A quadrilateral ABCD is called cyclic if all of its four vertices lie on a circle.
- In a cyclic quadrilateral the sum of opposite interior angles is 180 degrees.
- If the sum of a pair of opposite angles of a quadrilateral is 180, the quadrilateral is cyclic.
- In a cyclic quadrilateral the exterior angle is equal to interior opposite angle.
Notes for teachers
Activity#1 Cyclic quadrilateral
- Estimated Time 10 minutes
- Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any
- Circle and quadrilaterals should have been introduced.
- Multimedia resources : Laptop
- Website interactives/ links/ / Geogebra Applets
- Process:
- The teacher can recall the concept of a circle, quadrilateral, circumcircle.
- Can explain a cyclic quadrilateral and show the geogebra applet.
- Move points, the vertices of the quadrilateral and let the students observe the sum of opposite interior angles.
Developmental Questions:
- What two figures do you see in the figure ?
- Name the vertices of the quadrilateral.
- Where are all the 4 vertices situated ?
- Name the opposite interior angles of the quadrilateral.
- What do you observe about them.
- Evaluation:
- Compare the cyclic quadrilateral to circumcircle.
- Question Corner
- Can all quadrilaterals be cyclic ?
- What are the necessary conditions for a quadrilateral to be cyclic ?
Activity No # 2.Properties of a Cyclic quadrilateral
- Estimated Time: 45 minutes
- Materials/ Resources needed
coloured paper, pair of scissors, sketch pen, carbon paper, geometry box
- Prerequisites/Instructions, if any
- In a cyclic quadrilateral the sum of opposite interior angles is 180 degrees.
- In a cyclic quadrilateral the exterior angle is equal to interior opposite angle
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
This activity has been taken from the website http://mykhmsmathclass.blogspot.in/2007/11/class-ix-activity-16.html
- Process:
- Draw a circle of any radius on a coloured paper and cut it.
- Paste the circle cut out on a rectangular sheet of paper.
- By paper folding get chords AB, BC, CD and DA in order.
- Draw AB, BC, CD & DA. A cyclic quadrilateral ABCD is obtained.
- Produce AB to form a ray AE such that exterior angle CBE is formed.
- Make a replica of cyclic quadrilateral ABCD using carbon paper.
- Cut the replica into 4 parts such that each part contains one angle .
- Draw a straight line on a paper.
- Place the two opposite angles, angle BAD and angle BCD adjacent to each other on the straight line.Write the observation.
- Place other two opposite angles, angle ABC and angle ADC adjacent to each other on the straight line . Write the observation.
- Make a replica of angle ADC and place it on angle CBE . Write the observation.
Developmental Questions:
- How do you take radius ?
- What is the circumference ?
- What is a chord ?
- What is a quadrilateral ?
- Where are all four vertices of a quadrilateral located ?
- What part are we trying to cut and compare ?
- What can you infer ?
- Evaluation:
- Angle BAD and angle BCD, when placed adjacent to each other on a straight line, completely cover the straight angle.What does this mean ?
- Angle ABC and angle ADC, when placed adjacent to each other on a straight line, completely cover the straight angle.What can you conclude ?
- Compare angle ADC with angle CBE.
- Question Corner:
Name the two properties of cyclic quarilaterals.
Concept # 2.Construction of cyclic quadrilateral
Learning objectives
- Ability to construct a cyclic quadrilateral accurately .
Notes for teachers
Activity No # Constructing a cyclic quadrilateral
- Estimated Time: 40 minutes.
- Materials/ Resources needed:
- Laptop, geogebra file, projector and a pointer.
- Students constructing materials, the geometry box.
- white papers.
- Prerequisites/Instructions, if any
- Sufficient knowledge regarding construction of perpendicular lines, bisectors, angles and circle.
- Multimedia resources : Laptop
- Website interactives/ links/ / Geogebra Applets: For step by step illustration of cyclic quadrilateral construction please refer to the website: http://www.matrusrieppower.net/Constructionoftriangleandcyclicquadrilateral.html.
- Process:
- The teacher can do this activity after introducing the concept and properties of cyclic quadrilateral.
- She can project the file and let students watch it carefully.
- After watching discuss the steps of construction and the purpose of each step so that the students can appreciate the sequence of construction steps.
- Then ask the students to actually construct a cyclic quadrilateral for the given measures.
- Developmental Questions:
- What is a cyclic quadrilateral ? Why is it called so ?
- Name the measuring parameters of it ?
- What measures are given for its construction ?
- Explain the steps involved in determing the radius of the required circle ?
- What do the measures of the arcs specify ?
- Evaluation:
- Were the students able to justify the sequence of steps involved ?
- Question Corner:
- Can you draw a circle first and then the quadrilateral ? Why not so ?
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept # 3. Theorems on cyclic quadrilaterals
Learning objectives
- Both pairs of opposite angles of a cyclic quadrilateral are supplementary.
- When one side of a cyclic quadrilateral is produced, the exterior angle so formed is equal to the interior opposite angle.
Converse theorems:
- Suppose a quadrilateral is such that the sum of two opposite angles is a straight angle, them the quadrilateral is cyclic.
- If the exterior angle of a quadrilateral is equal to the interior opposite angle, then the quadrilateral is cyclic.
Notes for teachers
Activity No 1. Theorems
- Estimated Time : 40 minutes.
- Materials/ Resources needed:
Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any
- A cyclic quadrilateral and its properties.
- The linear pair and exterior angle theorem.
- The circle theorem (Angle at centre = double the angle at the circumference)
- Multimedia resources: Laptop
- Website interactives/ links/ / Geogebra Applets:
This geogebra file was done by ITfC-Edu-Team.
- Process:
- The teacher can project the geogebra file and prove the theorems.
- Developmental Questions:
- How many angles does a cyclic quadrilateral have ?
- Name the opposite angles of it.
- Name the minor arc.
- Recall the angle -arc theorem.
- What is the total angle at the centre of a circle ?
- Name the angles at the centre of the circle.
- What is the sum of those two angles ?
- How can you show that <b and <d are supplementary from above observations ?
- Evaluation;
- What is the converse of this theorem.
- Question Corner;
- Write down the steps to prove the converse of this theorem.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Hints for difficult problems
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template