Difference between revisions of "Angles"
KOER admin (talk | contribs) m (Text replacement - "<mm>[[" to "[[File:") |
Gurumurthy (talk | contribs) |
||
| (9 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
{| id="mp-topbanner" style="width:100%;font-size:100%;border-collapse:separate;border-spacing:20px;" | {| id="mp-topbanner" style="width:100%;font-size:100%;border-collapse:separate;border-spacing:20px;" | ||
|- | |- | ||
| − | |style="width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style="width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_History The Story of Mathematics] | [http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_History The Story of Mathematics] | ||
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Philosophy Philosophy of Mathematics] | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Philosophy Philosophy of Mathematics] |
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Pedagogy Teaching of Mathematics] | [http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Pedagogy Teaching of Mathematics] | ||
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
[http://karnatakaeducation.org.in/KOER/en/index.php/Maths:_Curriculum_and_Syllabus Curriculum and Syllabus] | [http://karnatakaeducation.org.in/KOER/en/index.php/Maths:_Curriculum_and_Syllabus Curriculum and Syllabus] | ||
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Topics Topics in School Mathematics] | [http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Topics Topics in School Mathematics] | ||
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
[http://karnatakaeducation.org.in/KOER/en/index.php/Text_Books#Mathematics_-_Textbooks Textbooks] | [http://karnatakaeducation.org.in/KOER/en/index.php/Text_Books#Mathematics_-_Textbooks Textbooks] | ||
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
[http://karnatakaeducation.org.in/KOER/en/index.php/Maths:_Question_Papers Question Bank] | [http://karnatakaeducation.org.in/KOER/en/index.php/Maths:_Question_Papers Question Bank] | ||
|} | |} | ||
While creating a resource page, please click here for a resource creation [http://karnatakaeducation.org.in/KOER/en/index.php/Resource_Creation_Checklist '''checklist''']. | While creating a resource page, please click here for a resource creation [http://karnatakaeducation.org.in/KOER/en/index.php/Resource_Creation_Checklist '''checklist''']. | ||
| + | |||
| + | === Concept Plan === | ||
| + | [[File:Angles.mm]] | ||
| + | <!-- This portal was created using subst:box portal skeleton --> | ||
| + | <!-- BANNER ACROSS TOP OF PAGE --> | ||
__FORCETOC__ | __FORCETOC__ | ||
| Line 33: | Line 34: | ||
= Teaching Outlines = | = Teaching Outlines = | ||
| − | ==Concept #1.What is an angle ? = | + | ====Concept #1.What is an angle ? ==== |
| − | + | ===Activities=== | |
| − | === | + | Foramtion of |
| − | |||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> | ''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> | ||
|} | |} | ||
| − | * | + | * |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Concept #2. Using a Protractor- Measuring an angle == | ==Concept #2. Using a Protractor- Measuring an angle == | ||
| Line 113: | Line 92: | ||
*Multimedia resources; Laptop | *Multimedia resources; Laptop | ||
*Website interactives/ links/ / Geogebra Applets | *Website interactives/ links/ / Geogebra Applets | ||
| − | < | + | <span> </span> |
| + | |||
| + | <span></span><div id="ggbContainer4a44ef2dc4b78417b74d34b3b537830b"></div><span></span> | ||
*Process: | *Process: | ||
# The teacher should recaptulate the concept of a point, line segment, ray, vertex and angles. | # The teacher should recaptulate the concept of a point, line segment, ray, vertex and angles. | ||
| Line 148: | Line 129: | ||
# Are angles <ABA' and <A'BA the same ? Justify | # Are angles <ABA' and <A'BA the same ? Justify | ||
# Differentiate between the zero angle and a complete angle. | # Differentiate between the zero angle and a complete angle. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Concept # 4. Angle constructions== | ==Concept # 4. Angle constructions== | ||
| Line 180: | Line 134: | ||
===Notes for teachers=== | ===Notes for teachers=== | ||
===Activity No # === | ===Activity No # === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Concept # 5. Angle bisector-Its construction== | ==Concept # 5. Angle bisector-Its construction== | ||
===Learning objectives=== | ===Learning objectives=== | ||
===Notes for teachers=== | ===Notes for teachers=== | ||
| − | + | Activity - [[Activity-construction of angles|Construction of angle with measure 22.5∘]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | This activity helps to illustrate the 'angle bisector' construction three times since we construct ∡22.5 by constructing ∡90∘ (bisecting a segment / straight angle ∡180∘, then bisect ∡90∘ to get ∡45∘ and finally bisect ∡45∘ to get ∡22.5∘). | |
| − | |||
| − | |||
| − | '' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Concept # 6. Pairs of angles== | ==Concept # 6. Pairs of angles== | ||
| Line 297: | Line 200: | ||
Laptop<br> | Laptop<br> | ||
'''*Website interactives/ links/ / Geogebra Applets'''<br> | '''*Website interactives/ links/ / Geogebra Applets'''<br> | ||
| − | < | + | <span> </span> |
| + | |||
| + | <span></span><div id="ggbContainer507e2592e2313aaf5f5d11fe1655c6bb"></div><span></span> | ||
| + | |||
| + | * This is a resource file on 'vertically opposite angles' | ||
| + | {{#widget:YouTube|id=m7v2g9_3BdU|left}}<br> | ||
| + | |||
| + | It has been created by Sucheta, Mathematics teacher, GHS Thyamangondlu | ||
| + | |||
'''*Process:''' | '''*Process:''' | ||
#Reiterate that when a transversal intersects parallel lines, several pairs of congruent and supplementary angles are formed. | #Reiterate that when a transversal intersects parallel lines, several pairs of congruent and supplementary angles are formed. | ||
| Line 378: | Line 289: | ||
#What is the supplement of 70 degrees? | #What is the supplement of 70 degrees? | ||
#Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines. | #Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= Hints for difficult problems = | = Hints for difficult problems = | ||
| Line 402: | Line 299: | ||
Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template | Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template | ||
| + | |||
| + | [[Category:Lines and Angles]] | ||
Latest revision as of 10:56, 2 November 2019
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Plan
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Useful websites
Reference Books
Teaching Outlines
Concept #1.What is an angle ?
Activities
Foramtion of
Concept #2. Using a Protractor- Measuring an angle
Learning objectives
Notes for teachers
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept #3.Types of angles
Learning objectives
Notes for teachers
Activity No #1.Crazy Angles using Geogebra
- Estimated Time: 40 minutes
- Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any:
- The students should have a basic understanding about point, rays, line segments and vertex.
- They should know how angles are formed.
- They should know that angles are measured in units called degrees. 360 ° is a full rotation (a circle)
- They should know to use a protractor and measure the angles.
- They should know the meaning of terms acute, obtuse, straight, reflex, and complete angles.
- Multimedia resources; Laptop
- Website interactives/ links/ / Geogebra Applets
- Process:
- The teacher should recaptulate the concept of a point, line segment, ray, vertex and angles.
- The teacher should show how angles are formed.
- Discuss the concept of cartesian plane, X and Y axes, rotation, and how it relates to angles.
- Demonstrate how to measure angles using a protractor.
- Define and illustrate the classification of the types of angles—acute, obtuse, right, straight zero and complete angles.
- In the succeeding class give the students protractors and let them have enough practise measuring and classifying angles.
Developmental Questions:
- What is a point ?
- A minimum of how many points are needed to define a line segment ?
- A minimum of how many points are needed to form an angle ?
- Name the line segments from the figure.
- What is a vertex ?
- How many rays /line segments are needed to form an angle ?
- Name the vertex at which the angle is formed
- Name the angle .
- Name the type of angle formed.
- Evaluation:
- Assess the students knowledge of angles by projecting different types of angles and asking them to name
- What are the characteristics of an acute angle ?
- What are the characteristics of an obtuse angle?
- What are the characteristics of a right angle
- Evaluate if the students have understood that :
- An angle is formed where 2 lines meet at a point.
- A right angle looks like a corner of a square or a rectangle.
- An acute angle is narrower than a right angle.
- An obtuse angle is wider than a right angle.
- Question Corner:
- What is an angle ?
- Where do you name an angle ?
- How do you identify different types of angles in 2-dimensional figures?
- How do angles help to classify 2-dimensional figures?
- Are angles <ABA' and <A'BA the same ? Justify
- Differentiate between the zero angle and a complete angle.
Concept # 4. Angle constructions
Learning objectives
Notes for teachers
Activity No #
Concept # 5. Angle bisector-Its construction
Learning objectives
Notes for teachers
Activity - Construction of angle with measure 22.5∘
This activity helps to illustrate the 'angle bisector' construction three times since we construct ∡22.5 by constructing ∡90∘ (bisecting a segment / straight angle ∡180∘, then bisect ∡90∘ to get ∡45∘ and finally bisect ∡45∘ to get ∡22.5∘).
Concept # 6. Pairs of angles
Learning objectives
Notes for teachers
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
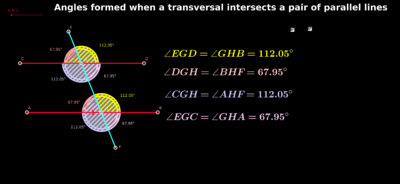
Concept # 7.Angles formed when lines are cut by a transversal
Learning objectives
Notes for teachers
Activity No # 1.Angles formed when a transversal intersects parallel lines
*Estimated Time : 40 minutes
*Materials/ Resources needed :Laptop, geogebra file, projector and pointer.
*Prerequisites/Instructions, if any :
- The students should have prior knowledge of parallel lines , transversal, angles and types of angles formed when a pair of parallel lines are intersected by a transversal.
- They should know what the terms interior, exterior, adjacent, alternate, consecutive, congruent, linear and corresponding mean.
- Students should know the definition of complementary angles, supplementary angles, and congruent angles.
*Multimedia resources:
Laptop
*Website interactives/ links/ / Geogebra Applets
- This is a resource file on 'vertically opposite angles'
It has been created by Sucheta, Mathematics teacher, GHS Thyamangondlu
*Process:
- Reiterate that when a transversal intersects parallel lines, several pairs of congruent and supplementary angles are formed.
- Have students draw two parallel lines and a third line(transversal) intersecting those two lines on their own paper. Direct them to think about any angle relationships they see. Have them discuss their conjectures with a partner.
- The teacher can next project the GeoGebra worksheet and discuss about types of angles and their relationships with the class .
- Finally the teacher and students can summarize together the angle relationshipsalong with their characteristics.
Linear pair of angles - adjacent and supplementary
- Vertical angles - congruent
- Corresponding angles -congruent
- Alternate interior angles - congruent
- Same side interior angles - supplementary
- Alternate exterior angles - congruent
- Same side exterior angles - supplementary
*Developmental Questions :(What discussion questions)
- How many pairs of corresponding angles are there ?
- What is true about corresponding angles formed when parallel lines are cut by a transversal?
- Compare different pairs of alternate interior angles. What do you notice?
- <EGD and <AHF are alternate exterior angles. What is another pair of alternate exterior angles?
- Compare different pairs of same-side interior angles. What do you notice?
- Compare different pairs of same-side exterior angles. What do you notice?
*Evaluation:
- What are the characteristics of linear angles (adjacent and supplementary) ?
- What do you observe about the angle measures of the linear angles?
*Question Corner:
- What do adjacent , alternate, linear , corresponding and consecutive mean individually
- What are complementary angles?
- What are supplementary angles ?
- What does it mean if two angles are congruent?
- What is the complement of 65 degrees
- What is the supplement of 70 degrees?
- Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines.
Activity No 2 Angles formed when a transversal intersects parallel lines
- Estimated Time : 90 minutes
- Materials/ Resources needed
Laptop, geogebra file, projector and pointer.
- Prerequisites/Instructions, if any
- The students should have prior knowledge of parallel lines , transversal, angles and types of angles formed when a pair of parallel lines are intersected by a transversal.
- They should know what the terms interior, exterior, adjacent, alternate, consecutive, congruent, linear and corresponding mean.
- Students should know the definition of complementary angles, supplementary angles, and congruent angles.
- Multimedia resources:
Laptop
- Website interactives/ links/ / Geogebra Applets
- Process
- Reiterate that when a transversal intersects parallel lines, several pairs of congruent and supplementary angles are formed.
- Have students draw two parallel lines and a third line(transversal) intersecting those two lines on their own paper. Direct them to think about any angle relationships they see. Have them discuss their conjectures with a partner.
- The teacher can next project the GeoGebra worksheet and discuss about types of angles and their relationships with the class .
- Finally the teacher and students can summarize together the angle relationships.
Linear pair of angles - adjacent and supplementary
Vertical angles - congruent
Corresponding angles -congruent
Alternate interior angles - congruent
Same side interior angles - supplementary
Alternate exterior angles - congruent
Same side exterior angles - supplementary
- Developmental Questions
- How many pairs of corresponding angles are there ?
- What is true about corresponding angles formed when parallel lines are cut by a transversal?
- Compare different pairs of alternate interior angles. What do you notice?
- <EGD and <AHF are alternate exterior angles. What is another pair of alternate exterior angles?
- Compare different pairs of same-side interior angles. What do you notice?
- Compare different pairs of same-side exterior angles. What do you notice?
Evaluation
- What are the characteristics of linear angles (adjacent and supplementary) ?
- What do you observe about the angle measures of the linear angles?
- Question Corner
- What do adjacent , alternate, linear , corresponding and consecutive mean individually
- What are complementary angles?
- What are supplementary angles ?
- What does it mean if two angles are congruent?
- What is the complement of 65 degrees
- What is the supplement of 70 degrees?
- Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines.
Hints for difficult problems
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template