Difference between revisions of "Number System"
CHaitra BS (talk | contribs) m (→Activities) |
Neeta Jose (talk | contribs) |
||
| (31 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | ''[http://karnatakaeducation.org.in/KOER/index.php/ಸಂಖ್ಯೆಗಳು ಕನ್ನಡದಲ್ಲಿ ನೋಡಿ]'' | |
| − | |||
| − | |||
| − | |||
| − | ''[http://karnatakaeducation.org.in/KOER/index.php/ಸಂಖ್ಯೆಗಳು ಕನ್ನಡದಲ್ಲಿ ನೋಡಿ]'' | ||
| − | |||
= Concept Map = | = Concept Map = | ||
[[File:Numbers.mm|Flash]] | [[File:Numbers.mm|Flash]] | ||
__FORCETOC__ | __FORCETOC__ | ||
| + | |||
| + | = Introduction = | ||
| + | <br> Our daily life is based on numbers. We use it for shopping, reckoning the time, counting distances and so on. Simple calculations seem effortless and trivial for most of our necessities.So we should know about numbers. Numbers help us count concrete objects. They help us to say which collection of objects . In this we are learning about basic operations of numbers - different types of numbers, representation, etc. <br> <br>[[File:Number system -Resource material_html_m3cabb6c3.png|400px]]<br><br> | ||
| + | How can math be so universal? First, human beings didn't invent math concepts; we discovered them. <br>Also, the language of math is numbers, not English or German or Russian. <br>If we are well versed in this language of numbers, it can help us make important decisions and perform everyday tasks. <br>Math can help us to shop wisely, understand population growth, or even bet on the horse with the best chance of winning the race. <br> | ||
| + | Mathematics expresses itself everywhere, in almost every face of life - in nature all around us, and in the technologies in our hands. Mathematics is the language of science and engineering - describing our understanding of all that we observe.Mathematics has been around since the beginnings of time and it most probably began with counting. Many, if not all puzzles and games require mathematical logic and deduction. This section uses the fun and excitement of various popular games and puzzles, and the exhilaration of solving them, to attract and engage the students to realise the mathematics in fun and games. <br><br> | ||
| + | '''Descriptive Statement''' | ||
| + | <br>Number sense is defined as an intuitive feel for numbers and a common sense approach to using them. It is a comfort with what numbers represent, coming from investigating their characteristics and using them in diverse situations, and how best they can be used to describe a particular situation. Number sense is an attribute of all successful users of mathematics. Our students often do not connect what is happening in their mathematics classrooms with their daily lives. It is essential that the mathematics curriculum build on the sense of number that students bring with them to school. Problems and numbers which arise in the context of the students world are more meaningful to students than traditional textbook exercises and help them develop their sense of how numbers and operations are used. Frequent use of estimation and mental computation are also important ingredients in the development of number sense, as are regular opportunities for student communication. Discussion of their own invented strategies for problem solutions helps students strengthen their intuitive understanding of numbers and the relationships between numbers.<br><br> | ||
| + | In summary, the commitment to develop number sense requires a dramatic shift in the way students learn mathematics. | ||
| + | |||
| + | = Flow Chart = | ||
| + | [[File:Number system -Resource material_html_m65980570.jpg|400px]] | ||
= Textbook = | = Textbook = | ||
| Line 18: | Line 24: | ||
Watch the following video on the story of how numbers evolved. The video called Story of One tells how numbers evolved and the initial questions around number theory.<br> | Watch the following video on the story of how numbers evolved. The video called Story of One tells how numbers evolved and the initial questions around number theory.<br> | ||
| − | {{#widget:YouTube|id= | + | {{#widget:YouTube|id=jrLQW1vQklE}} |
This video is related to number system, helps to know the basic information about number system | This video is related to number system, helps to know the basic information about number system | ||
| Line 24: | Line 30: | ||
{{#widget:YouTube|id=bj4EKEfrKOU}} | {{#widget:YouTube|id=bj4EKEfrKOU}} | ||
| + | This video is related to irrational numbers by Suchitha | ||
| + | |||
| + | {{#widget:YouTube|id=udKD4yxsWe4}} | ||
| + | |||
| + | This video is relating to exploring number patterns in square numbers. | ||
| + | |||
| + | {{Youtube|MoM2jw7W-ms | ||
| + | }} | ||
==Reference Books== | ==Reference Books== | ||
| Line 29: | Line 43: | ||
*[http://karnatakaeducation.org.in/KOER/en/index.php/Number_bases_activity_1 Number based activity] | *[http://karnatakaeducation.org.in/KOER/en/index.php/Number_bases_activity_1 Number based activity] | ||
==Concept #1 - History of Numbers: Level 0 == | ==Concept #1 - History of Numbers: Level 0 == | ||
| + | The following website takes us on a fascinating journey originating from Prehistoric Mathematics, its evolution in various civilizations such as Egyptian, Greek, Indian, Chinese etc. to the increased complexities and abstractions of the modern era mathematics. This story of history of numbers also includes descriptions related to contributions of some of the important men and women to the development of mathematics. | ||
| + | |||
| + | '''http://storyofmathematics.com/story.html''' | ||
===Learning objectives=== | ===Learning objectives=== | ||
#What is the story of numbers? | #What is the story of numbers? | ||
| Line 38: | Line 55: | ||
===Activities=== | ===Activities=== | ||
| − | # [[ | + | # Series of Activities in one page- [[Series of Activities on Number Systems|Click Here]] |
#Activity 1 | #Activity 1 | ||
| Line 57: | Line 74: | ||
===Activities=== | ===Activities=== | ||
#Activity 1 - [[Quantity and Numbers|Quantity and Numbers]] | #Activity 1 - [[Quantity and Numbers|Quantity and Numbers]] | ||
| − | #[[The_eighth_donkey_story_for_number_sense|The Eighth Donkey Story]] | + | #Activity 2 - [[The_eighth_donkey_story_for_number_sense|The Eighth Donkey Story]] |
| − | #Activity | + | #Activity 3 - [[Cardinal and Ordinal Numbers]] |
==Concept #3 The Number Line :Level 1-2 == | ==Concept #3 The Number Line :Level 1-2 == | ||
| + | The number line is not just a school object. It is as much a mathematical idea as functions. | ||
| + | The number line is a geometric “model” of all numbers -- including 0 1, 2, 25, 374 trillion, and -5, Unlike counters, which model only counters, the number line models measurement, which is why it must start with zero. (When we count, the first object we touch is called "one." When we measur using a ruler, we line one end of the object we’re measuring against the zero mark on the ruler. | ||
| + | |||
| + | <br>[[File:Number system -Resource material_html_1de463c.jpg|400px]]<br> | ||
| + | |||
| + | Part of the power of addition and subtraction is that these operations work with both counting and measuring. Therefore, to understand basic operations like addition and subtraction, we need a number line model as well as counters. | ||
===Objectives=== | ===Objectives=== | ||
#Numbers can be represented on a continuum called a number line | #Numbers can be represented on a continuum called a number line | ||
| Line 70: | Line 93: | ||
===Activities=== | ===Activities=== | ||
| − | #Activity 1 - [[Hopping_on_number_line|To introduce Number line]] | + | #Activity 1- Add,Sub,Product,Sum,Hopping - [[Hopping_on_number_line|To introduce Number line]] |
| − | #Activity 2 - [[Operations_on_number_lines_1|Sum | + | #Activity 2 - [[Operations_on_number_lines_1|Sum of numbers]] |
#Activity 3 - [[Building_the_number_line|Classroom number line]] | #Activity 3 - [[Building_the_number_line|Classroom number line]] | ||
| Line 83: | Line 106: | ||
#Activity 2 - [http://karnatakaeducation.org.in/KOER/en/index.php/Number_bases_activity_2 Activity-2] | #Activity 2 - [http://karnatakaeducation.org.in/KOER/en/index.php/Number_bases_activity_2 Activity-2] | ||
| − | ==Concept # | + | ==Concept #5 Place Value== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === Learning objectives === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Notes for teachers=== | ===Notes for teachers=== | ||
''These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.'' | ''These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.'' | ||
| Line 219: | Line 116: | ||
#Activity 1 [http://karnatakaeducation.org.in/KOER/en/index.php/Place_value_activity_1 Activity-1] | #Activity 1 [http://karnatakaeducation.org.in/KOER/en/index.php/Place_value_activity_1 Activity-1] | ||
#Activity 2 [http://karnatakaeducation.org.in/KOER/en/index.php/Place_value_activity_2 Activity-2] | #Activity 2 [http://karnatakaeducation.org.in/KOER/en/index.php/Place_value_activity_2 Activity-2] | ||
| + | <br> | ||
| − | ==Concept # | + | ==Concept #6 Negative numbers are the opposite of positive numbers - == |
=== Objectives === | === Objectives === | ||
# To extend the understanding and skill of representing symbolically numbers and manipulating them.<br> | # To extend the understanding and skill of representing symbolically numbers and manipulating them.<br> | ||
# To understand that negative numbers are numbers that are created to explain situations in such a way that mathematical operations hold<br> | # To understand that negative numbers are numbers that are created to explain situations in such a way that mathematical operations hold<br> | ||
| − | # | + | # To recognize that negative numbers are opposite of positive numbers; the rules of working with negative numbers are opposite to that of working with positive numbers<br> |
| − | # Together, the negative numbers and positive numbers form one | + | # Together, the negative numbers and positive numbers form one continuous number line<br> |
# Perform manipulations with negative numbers and express symbolically situations involving negative numbers<br> | # Perform manipulations with negative numbers and express symbolically situations involving negative numbers<br> | ||
| Line 236: | Line 134: | ||
#Activity 1 -[[What are negative numbers|What are negative numbers]] | #Activity 1 -[[What are negative numbers|What are negative numbers]] | ||
| − | + | == Concept #7 : Types of Numbers == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === Learning objectives === | |
| − | + | [[Types of numbers|Types of Numbers]] | |
| − | |||
| − | |||
| − | |||
| − | + | === Notes for teachers === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | === Activities === | ||
| − | + | = Assessment activities= | |
| − | + | '''I Fill number line (1 period)'''<br> | |
| − | + | Draw these one below the other<br> | |
| + | 1,2,.......<br> | ||
| + | 10,20,.......<br> | ||
| + | 100, 200,.....<br> | ||
| − | + | '''II Tell stories and Play With Number Systems (1 period - optional)'''<br> | |
| + | http://www.math.wichita.edu/history/topics/num-sys.html#sense<br> | ||
| + | (This page is downloaded and given as reading materials – page is called Number Systems)<br> | ||
| − | + | '''III Questions/ activities for class'''<br> | |
| − | + | #Arrange in order – shortest, tallest, increasing and decreasing order<br> | |
| − | + | [[File:Tallest.png|400px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= Hints for difficult problems = | = Hints for difficult problems = | ||
| Line 289: | Line 167: | ||
Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template | Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template | ||
| + | |||
| + | [[Category:Number system]] | ||
Latest revision as of 10:05, 23 July 2021
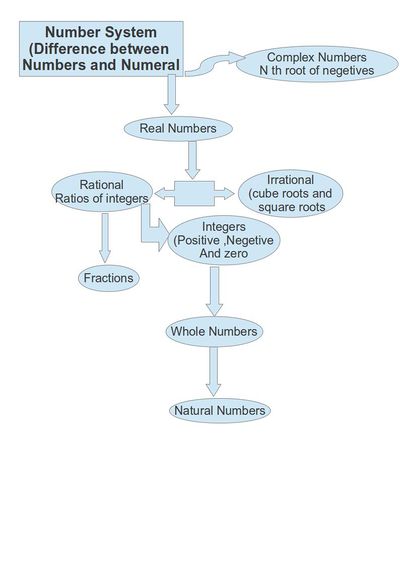
Concept Map
Introduction
Our daily life is based on numbers. We use it for shopping, reckoning the time, counting distances and so on. Simple calculations seem effortless and trivial for most of our necessities.So we should know about numbers. Numbers help us count concrete objects. They help us to say which collection of objects . In this we are learning about basic operations of numbers - different types of numbers, representation, etc.

How can math be so universal? First, human beings didn't invent math concepts; we discovered them.
Also, the language of math is numbers, not English or German or Russian.
If we are well versed in this language of numbers, it can help us make important decisions and perform everyday tasks.
Math can help us to shop wisely, understand population growth, or even bet on the horse with the best chance of winning the race.
Mathematics expresses itself everywhere, in almost every face of life - in nature all around us, and in the technologies in our hands. Mathematics is the language of science and engineering - describing our understanding of all that we observe.Mathematics has been around since the beginnings of time and it most probably began with counting. Many, if not all puzzles and games require mathematical logic and deduction. This section uses the fun and excitement of various popular games and puzzles, and the exhilaration of solving them, to attract and engage the students to realise the mathematics in fun and games.
Descriptive Statement
Number sense is defined as an intuitive feel for numbers and a common sense approach to using them. It is a comfort with what numbers represent, coming from investigating their characteristics and using them in diverse situations, and how best they can be used to describe a particular situation. Number sense is an attribute of all successful users of mathematics. Our students often do not connect what is happening in their mathematics classrooms with their daily lives. It is essential that the mathematics curriculum build on the sense of number that students bring with them to school. Problems and numbers which arise in the context of the students world are more meaningful to students than traditional textbook exercises and help them develop their sense of how numbers and operations are used. Frequent use of estimation and mental computation are also important ingredients in the development of number sense, as are regular opportunities for student communication. Discussion of their own invented strategies for problem solutions helps students strengthen their intuitive understanding of numbers and the relationships between numbers.
In summary, the commitment to develop number sense requires a dramatic shift in the way students learn mathematics.
Flow Chart
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Useful websites
Watch the following video on the story of how numbers evolved. The video called Story of One tells how numbers evolved and the initial questions around number theory.
This video is related to number system, helps to know the basic information about number system
This video is related to irrational numbers by Suchitha
This video is relating to exploring number patterns in square numbers.
Reference Books
Teaching Outlines
Concept #1 - History of Numbers: Level 0
The following website takes us on a fascinating journey originating from Prehistoric Mathematics, its evolution in various civilizations such as Egyptian, Greek, Indian, Chinese etc. to the increased complexities and abstractions of the modern era mathematics. This story of history of numbers also includes descriptions related to contributions of some of the important men and women to the development of mathematics.
http://storyofmathematics.com/story.html
Learning objectives
- What is the story of numbers?
- How did counting begin and learning distinguish between the quantity 2 and the number 2.
- The number "2" is an abstraction of the quantity
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Series of Activities in one page- Click Here
- Activity 1
Concept #2 Number Sense and Counting : Level 0
Objectives
1. Understand that there is an aspect of quantity that we can develop with disparate objects
2. Comparison and mapping of quantities (more or less or equal)
3. Representation of quantity by numbers and learning the abstraction that “2 represents quantity 2 of a given thing”
4. Numbers also have an ordinal value – that of ordering and that is different from the representation aspect of numbers
5. Expression of quantities and manipulation of quantities (operations) symbolically
6. Recognizing the quantity represented by numerals and discovering how one number is related to another number
7. This number representation is continuous.
Notes for teachers
This is not one period – but a lesson topic. There could be a few more lessons in this section. For example, for representing collections and making a distinction between 1 apple and a dozen apples. This idea could be explained later to develop fractions. Another activity that can also be used to talk of units of measure. Addition and subtraction have been discussed here – extend this to include multiplication and division).
Activities
- Activity 1 - Quantity and Numbers
- Activity 2 - The Eighth Donkey Story
- Activity 3 - Cardinal and Ordinal Numbers
Concept #3 The Number Line :Level 1-2
The number line is not just a school object. It is as much a mathematical idea as functions. The number line is a geometric “model” of all numbers -- including 0 1, 2, 25, 374 trillion, and -5, Unlike counters, which model only counters, the number line models measurement, which is why it must start with zero. (When we count, the first object we touch is called "one." When we measur using a ruler, we line one end of the object we’re measuring against the zero mark on the ruler.
Part of the power of addition and subtraction is that these operations work with both counting and measuring. Therefore, to understand basic operations like addition and subtraction, we need a number line model as well as counters.
Objectives
- Numbers can be represented on a continuum called a number line
- Number line is a representation; geometric model of all numbers
- Mathematical operations can b explained by moving along the number line
Notes for teachers
Introduce the number line as a concept by itself as well as a method to count, measure and perform arithmetic operations by moving along the number line through different activities.
Activities
- Activity 1- Add,Sub,Product,Sum,Hopping - To introduce Number line
- Activity 2 - Sum of numbers
- Activity 3 - Classroom number line
Concept #4 Number Bases
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Activity 1 - Activity-1
- Activity 2 - Activity-2
Concept #5 Place Value
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activities
- Activity 1 Activity-1
- Activity 2 Activity-2
Concept #6 Negative numbers are the opposite of positive numbers -
Objectives
- To extend the understanding and skill of representing symbolically numbers and manipulating them.
- To understand that negative numbers are numbers that are created to explain situations in such a way that mathematical operations hold
- To recognize that negative numbers are opposite of positive numbers; the rules of working with negative numbers are opposite to that of working with positive numbers
- Together, the negative numbers and positive numbers form one continuous number line
- Perform manipulations with negative numbers and express symbolically situations involving negative numbers
Notes for teachers
Negative numbers are to be introduced as a type of number; they do the opposite of what positive numbers do.
Read the activity for more detailed description.
Activities
- Activity 1 -What are negative numbers
Concept #7 : Types of Numbers
Learning objectives
Notes for teachers
Activities
Assessment activities
I Fill number line (1 period)
Draw these one below the other
1,2,.......
10,20,.......
100, 200,.....
II Tell stories and Play With Number Systems (1 period - optional)
http://www.math.wichita.edu/history/topics/num-sys.html#sense
(This page is downloaded and given as reading materials – page is called Number Systems)
III Questions/ activities for class
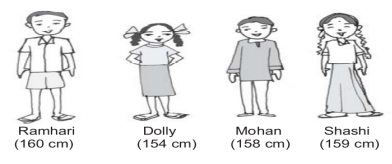
- Arrange in order – shortest, tallest, increasing and decreasing order
Hints for difficult problems
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template