Difference between revisions of "Polygons"
| (43 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#ffffff; vertical-align:top; text-align:center; padding:5px;"> | ||
| + | ''[http://karnatakaeducation.org.in/KOER/index.php/ಬಹು_ಭುಜಾಕೃತಿಗಳು ಕನ್ನಡದಲ್ಲಿ ನೋಡಿ]''</div> | ||
<!-- This portal was created using subst:box portal skeleton --> | <!-- This portal was created using subst:box portal skeleton --> | ||
<!-- BANNER ACROSS TOP OF PAGE --> | <!-- BANNER ACROSS TOP OF PAGE --> | ||
{| id="mp-topbanner" style="width:100%;font-size:100%;border-collapse:separate;border-spacing:20px;" | {| id="mp-topbanner" style="width:100%;font-size:100%;border-collapse:separate;border-spacing:20px;" | ||
|- | |- | ||
| − | |style="width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style="width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
| − | [http:// | + | [http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_History The Story of Mathematics] |
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|[http:// | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Philosophy Philosophy of Mathematics] |
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
| − | [http:// | + | [http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Pedagogy Teaching of Mathematics] |
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
| − | [http:// | + | [http://karnatakaeducation.org.in/KOER/en/index.php/Maths:_Curriculum_and_Syllabus Curriculum and Syllabus] |
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
| − | [http:// | + | [http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Topics Topics in School Mathematics] |
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
| − | [http:// | + | [http://karnatakaeducation.org.in/KOER/en/index.php/Text_Books#Mathematics_-_Textbooks Textbooks] |
| − | |style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "| | + | | style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " | |
| − | [http:// | + | [http://karnatakaeducation.org.in/KOER/en/index.php/Maths:_Question_Papers Question Bank] |
|} | |} | ||
While creating a resource page, please click here for a resource creation [http://karnatakaeducation.org.in/KOER/en/index.php/Resource_Creation_Checklist '''checklist''']. | While creating a resource page, please click here for a resource creation [http://karnatakaeducation.org.in/KOER/en/index.php/Resource_Creation_Checklist '''checklist''']. | ||
| − | + | ==Concept map== | |
| − | = Textbook = | + | {{#drawio:mmPolygons|interactive}} |
| + | |||
| + | == Textbook == | ||
To add textbook links, please follow these instructions to: | To add textbook links, please follow these instructions to: | ||
([{{fullurl:{{FULLPAGENAME}}/textbook|action=edit}} Click to create the subpage]) | ([{{fullurl:{{FULLPAGENAME}}/textbook|action=edit}} Click to create the subpage]) | ||
| − | =Additional Information= | + | ==Additional Information== |
| − | ==Useful websites== | + | === Resources === |
| + | |||
| + | ==== Resource Title ==== | ||
| + | [http://www.mathopenref.com/tocs/polygontoc.html Polygons] | ||
| + | |||
| + | ===Useful websites=== | ||
1. http://www.wyzant.com/resources/lessons/math/geometry/quadrilaterals/polygons . This website is good for referring to the theory regarding polygons. | 1. http://www.wyzant.com/resources/lessons/math/geometry/quadrilaterals/polygons . This website is good for referring to the theory regarding polygons. | ||
| − | ==Reference Books== | + | ===Reference Books=== |
| − | = Teaching Outlines = | + | == Teaching Outlines == |
# Introduction to polygon | # Introduction to polygon | ||
| Line 36: | Line 45: | ||
# Characteristics of polygons. | # Characteristics of polygons. | ||
# Types of polygons. | # Types of polygons. | ||
| + | |||
| + | ==Building prior competencies== | ||
| + | Many student are entering Class 9 without adequate understanding of prior concepts like angles, line, etc. | ||
| + | Therefore, the following sequence of lessons has been suggested with a combination of hands-on activities, Geogebra work to build those concepts in students. | ||
| + | [[File:Polygon_prior_competencies_upload.mm|flash]] | ||
| + | |||
| + | The following Geogebra files are used with associated lessons: | ||
| + | #[[:File:0. Angles introduction.ggb|Angles introduction]] | ||
| + | #[[:File:1. Complementary angles demonstration.ggb|Complementary angles]] | ||
| + | #[[:File:2. Supplementary angles demonstration.ggb|Supplementary angles]] | ||
| + | #[[:File:3. parallellines-2.ggb|Activity with parallel line]] | ||
| + | #[[:File:4. Introduction to a triangle.ggb|Demonstration of triangle]] | ||
| + | #[[:File:5. Introduction to a polygon.ggb|Polygon]] | ||
| + | |||
==Concept #1. Introduction to polygons and nomenclature.== | ==Concept #1. Introduction to polygons and nomenclature.== | ||
===Learning objectives=== | ===Learning objectives=== | ||
| Line 48: | Line 71: | ||
==Notes for teachers== | ==Notes for teachers== | ||
| − | There are a countless number of polygons. Because they all differ in the number of sides that they have, this results in different angle measures at their vertices. Listed below are the names and number of sides of some polygons. The "Interior Angle Measure" column of the table only applies to regular polygons, in which all the interior angles are equal.<br> | + | Source: This information has been taken from the website :http://www.wyzant.com/resources/lessons/math/geometry/quadrilaterals/polygons<br> |
| + | Summary: There are a countless number of polygons. Because they all differ in the number of sides that they have, this results in different angle measures at their vertices. Listed below are the names and number of sides of some polygons. The "Interior Angle Measure" column of the table only applies to regular polygons, in which all the interior angles are equal.<br> | ||
With the exception of the triangle and quadrilateral, notice that all polygon names end with "gon." What sets regular polygon names apart from each other are their prefixes, which speak to the number of sides that they have. For instance, the prefix for the word "hexagon" is "hexa," which essentially means "six." However, as we move down our list and the names for polygons becomes quite confusing, we need a more efficient way of naming polygons. One way is by not calling a polygon by its real name, but rather by just saying the number of sides it has, and attaching "-gon" at the end. For instance, rather than calling an 18-sided polygon an "octdecagon," we can just call it an 18-gon. Thus, a polygon with n sides is simply called an n-gon. | With the exception of the triangle and quadrilateral, notice that all polygon names end with "gon." What sets regular polygon names apart from each other are their prefixes, which speak to the number of sides that they have. For instance, the prefix for the word "hexagon" is "hexa," which essentially means "six." However, as we move down our list and the names for polygons becomes quite confusing, we need a more efficient way of naming polygons. One way is by not calling a polygon by its real name, but rather by just saying the number of sides it has, and attaching "-gon" at the end. For instance, rather than calling an 18-sided polygon an "octdecagon," we can just call it an 18-gon. Thus, a polygon with n sides is simply called an n-gon. | ||
| Line 54: | Line 78: | ||
| − | |||
===Activity No # 1. Which polygon am I ? === | ===Activity No # 1. Which polygon am I ? === | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
| − | ''[http:// | + | ''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> |
|} | |} | ||
*Estimated Time: 30 minutes. | *Estimated Time: 30 minutes. | ||
*Materials/ Resources needed: Laptop, geogebra file, projector and a pointer. | *Materials/ Resources needed: Laptop, geogebra file, projector and a pointer. | ||
*Prerequisites/Instructions, if any: | *Prerequisites/Instructions, if any: | ||
| − | # | + | # Lines intersect to form figures. |
| − | # | + | # Plane closed figures have atleast 3 sides. |
# The intersecting points of two lines is known as a vertex and the lines are the edges/sides. | # The intersecting points of two lines is known as a vertex and the lines are the edges/sides. | ||
| − | # | + | # Meaning of greek numerals uni, bi, tri ....etc. |
*Multimedia resources: Laptop | *Multimedia resources: Laptop | ||
| − | *Website interactives/ links/ / Geogebra Applets | + | *Website interactives/ links/ / Geogebra Applets: This geogebra file has been created by '''Smt Sarah Zakiya Madam, GUHS, Yellagondapalya.''' |
| + | <span> </span> | ||
| + | |||
| + | <span></span><div id="ggbContainerfbad5ae84c119793e6125f6c6fe3c642"></div><span></span> | ||
*Process: | *Process: | ||
# The teacher can tell the students that they are surrounded by many different kinds of shapes every day. | # The teacher can tell the students that they are surrounded by many different kinds of shapes every day. | ||
| Line 92: | Line 118: | ||
# What is a polygon with 12 sides called ? | # What is a polygon with 12 sides called ? | ||
# You have a collection of sides from triangles and decagons. The total number of sides is 100 and you have 4 decagons. How many triangles do you have ? | # You have a collection of sides from triangles and decagons. The total number of sides is 100 and you have 4 decagons. How many triangles do you have ? | ||
| − | |||
===Activity No # === | ===Activity No # === | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
| − | ''[http:// | + | ''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> |
|} | |} | ||
*Estimated Time | *Estimated Time | ||
| Line 108: | Line 133: | ||
*Question Corner | *Question Corner | ||
| − | ==Concept #2. | + | ==Concept #2. Properties and measurements of polygons== |
===Learning objectives=== | ===Learning objectives=== | ||
| + | # The sum of the interior angle measures of an n-sided, convex polygon is <math>(n-2).180</math> | ||
| + | # A regular polygon has all sides and angles equal. | ||
| + | # All exterior angles of a polygon add upto 360 degrees. | ||
| + | # Each exterior angle must be <math>360/n</math> | ||
| + | # Each of the exterior angle and interior angles are measured from the same line. hence they add upto 180 degrees. | ||
| + | # Area of Polygon = perimeter × apothem / 2 [[File:Apothem.jpeg|150px]] | ||
| + | |||
| + | |||
| + | (This image has been taken from:http://www.mathsisfun.com/geometry/regular-polygons.html) | ||
| + | |||
===Notes for teachers=== | ===Notes for teachers=== | ||
| − | ===Activity No # === | + | ===Activity No # 1. Polygon's table of values.=== |
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
| − | [http:// | + | [http://karnatakaeducation.org.in/?q=node/305 Click to Comment]</div> |
|} | |} | ||
| − | *Estimated Time: | + | *Estimated Time: 90 minutes. |
*Materials/ Resources needed: | *Materials/ Resources needed: | ||
| + | # Sheets of paper, scale, compass, protractor, pencil. | ||
*Prerequisites/Instructions, if any: | *Prerequisites/Instructions, if any: | ||
| + | # Knowledge of different polygons and their names. | ||
| + | # Requisite formulae needed to do the calculations. | ||
| + | # Skills to perform and tabulate calculations accurately. | ||
*Multimedia resources: | *Multimedia resources: | ||
*Website interactives/ links/ / Geogebra Applets: | *Website interactives/ links/ / Geogebra Applets: | ||
| − | *Process | + | Please refer to this website for more clarity on this activity : http://www.mathsisfun.com/geometry/regular-polygons.html |
| + | *Process: | ||
| + | # Use the formulas listed in learning objectives above to make a table of Side, Apothem and Area, compared to a Radius of "1": | ||
| + | # Let the table have the following columns. | ||
| + | |||
| + | [[File:Table.jpeg|800px]] | ||
| + | |||
| + | *Developmental Questions: | ||
| + | # Name the types of polygons based on their sides. | ||
| + | # What is a regular polygon ? | ||
| + | # How many sides does a ______________ have ? | ||
| + | # What is an interior angle ? | ||
| + | # Is there any relationship between the number of sides and number of angles ? | ||
| + | # What radius has been mentioned here as common for all ? | ||
| + | # What is an apothem ? | ||
| + | # How do you get the central point of a polygon ? | ||
| + | # What is the formula to find the area of a polygon ? | ||
*Evaluation: | *Evaluation: | ||
| − | *Question Corner | + | # Which measuring parameter do you think is the deciding factor for the area of a polygon ? |
| + | *Question Corner | ||
| + | # Can you find the listed measures like interior angle, area without using the formula ? How ? Discuss. | ||
===Activity No # === | ===Activity No # === | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
| − | ''[http:// | + | ''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> |
|} | |} | ||
*Estimated Time | *Estimated Time | ||
| Line 151: | Line 208: | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
| − | ''[http:// | + | ''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> |
|} | |} | ||
| − | [[File:Tangram.jpg| | + | [[File:Tangram.jpg|300px]] |
| + | |||
*Estimated Time : 40 minutes. | *Estimated Time : 40 minutes. | ||
*Materials/ Resources needed: Chart papers, scissors, pencil, scale. | *Materials/ Resources needed: Chart papers, scissors, pencil, scale. | ||
*Prerequisites/Instructions, if any | *Prerequisites/Instructions, if any | ||
| − | # | + | # An understanding of basic shapes like square, rectangle, parallelogram, triangle and trapezium. |
| − | # | + | # Ability to draw mentioned shapes accurately and cut exactly on boundaries. |
*Multimedia resources | *Multimedia resources | ||
*Website interactives/ links/ / Geogebra Applets | *Website interactives/ links/ / Geogebra Applets | ||
| Line 164: | Line 222: | ||
# This is a very old Chinese puzzle known as a tangram. | # This is a very old Chinese puzzle known as a tangram. | ||
# Cut out the square below into 7 shapes. | # Cut out the square below into 7 shapes. | ||
| − | # Cut out the 7 shapes and rearrange them to form: | + | # Cut out the 7 shapes and rearrange them to form:<br> |
| − | (a) a square from two triangles, and then change it to a parallelogram; | + | (a) a square from two triangles, and then change it to a parallelogram;<br> |
| − | (b) a rectangle using three pieces, and then change it into a parallelogram; | + | (b) a rectangle using three pieces, and then change it into a parallelogram;<br> |
| − | (c) a trapezium with three pieces; | + | (c) a trapezium with three pieces;<br> |
| − | (d) a parallelogram with four pieces; | + | (d) a parallelogram with four pieces;<br> |
| − | (e) a trapezium from the square, parallelogram and the two small triangles; | + | (e) a trapezium from the square, parallelogram and the two small triangles;<br> |
| − | (f) a triangle with three pieces; | + | (f) a triangle with three pieces;<br> |
| − | (g) a rectangle with all seven pieces. | + | (g) a rectangle with all seven pieces.<br> |
| − | (h) a kite with two traingles. | + | (h) a kite with two traingles.<br> |
| − | + | 4. Finally, put the pieces back together to form the original square.<br> | |
*Developmental Questions: | *Developmental Questions: | ||
# Were you all able to read and follow the instructions. | # Were you all able to read and follow the instructions. | ||
| Line 188: | Line 246: | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
| − | ''[http:// | + | ''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> |
|} | |} | ||
*Estimated Time: | *Estimated Time: | ||
| Line 202: | Line 260: | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
| − | ''[http:// | + | ''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> |
|} | |} | ||
*Estimated Time | *Estimated Time | ||
| Line 214: | Line 272: | ||
= Hints for difficult problems = | = Hints for difficult problems = | ||
| + | [[:File:polygon problem.odt]] | ||
| + | ==Angle sum property== | ||
| + | CLASS IX TOPIC POLYGONS | ||
| + | ADDITIONAL PROBLEMS (problem no 3 ) | ||
| + | A polygon has 'n' sides .Two of it's angles are right angles and each of remaining angle isFind the value of 'n'. | ||
| + | Step 1;(Students must understand the problem) | ||
| + | In a polygon of side 'n' two angles are and other angles are each. We must find out value of 'n'. | ||
| + | Step 2(Students know the formula for sum of angles of polygon of side 'n') | ||
| + | (2n-4)right angles. | ||
| + | Step 3(Sum of the angles is equal to what?) | ||
| + | There are 'n' angles in a polygon of side 'n'.Out of 'n' angles 2 angles are right anles and other (n-2) angles are each. | ||
| + | |||
| + | (2n-4) <math>90^0</math> = (n-2)<nowiki><math>\144^0+(2)(90^0)how to open the bracket and substitute the values)</nowiki> | ||
| + | |||
| + | 2n x - 4 x = | ||
| + | |||
| + | = (Brings similar terms at one side of the equation) | ||
| + | |||
| + | = (Add and substract and simplify) | ||
| + | |||
| + | = | ||
| + | |||
| + | n = (Devide and simplify) | ||
| + | |||
| + | n = 7 | ||
= Project Ideas = | = Project Ideas = | ||
| Line 222: | Line 305: | ||
Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template | Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template | ||
| + | |||
| + | [[Category:Polygons]] | ||
Latest revision as of 13:01, 5 July 2022
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept map
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Resources
Resource Title
Useful websites
1. http://www.wyzant.com/resources/lessons/math/geometry/quadrilaterals/polygons . This website is good for referring to the theory regarding polygons.
Reference Books
Teaching Outlines
- Introduction to polygon
- Naming the polygons
- Characteristics of polygons.
- Types of polygons.
Building prior competencies
Many student are entering Class 9 without adequate understanding of prior concepts like angles, line, etc. Therefore, the following sequence of lessons has been suggested with a combination of hands-on activities, Geogebra work to build those concepts in students.
The following Geogebra files are used with associated lessons:
- Angles introduction
- Complementary angles
- Supplementary angles
- Activity with parallel line
- Demonstration of triangle
- Polygon
Concept #1. Introduction to polygons and nomenclature.
Learning objectives
- Lines intersect to form figures.
- Two dimensional closed figures can be of varied shapes.
- Plane closed figures with ≥ 3 sides are known as polygons.
- They can be defined as two-dimensional, closed, plane shapes composed of a finite number of straight sides that meet at points called vertices.
- There are a countless number of polygons.
- Because they all differ in the number of sides that they have, this results in different angle measures at their vertices.
- With the exception of the triangle and quadrilateral, all polygon names end with "gon."
- Generally polygons are named with their number of sides as prefixes. The prefix for the word "hexagon" is "hexa," which essentially means "six."
Notes for teachers
Source: This information has been taken from the website :http://www.wyzant.com/resources/lessons/math/geometry/quadrilaterals/polygons
Summary: There are a countless number of polygons. Because they all differ in the number of sides that they have, this results in different angle measures at their vertices. Listed below are the names and number of sides of some polygons. The "Interior Angle Measure" column of the table only applies to regular polygons, in which all the interior angles are equal.
With the exception of the triangle and quadrilateral, notice that all polygon names end with "gon." What sets regular polygon names apart from each other are their prefixes, which speak to the number of sides that they have. For instance, the prefix for the word "hexagon" is "hexa," which essentially means "six." However, as we move down our list and the names for polygons becomes quite confusing, we need a more efficient way of naming polygons. One way is by not calling a polygon by its real name, but rather by just saying the number of sides it has, and attaching "-gon" at the end. For instance, rather than calling an 18-sided polygon an "octdecagon," we can just call it an 18-gon. Thus, a polygon with n sides is simply called an n-gon.
Activity No # 1. Which polygon am I ?
- Estimated Time: 30 minutes.
- Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any:
- Lines intersect to form figures.
- Plane closed figures have atleast 3 sides.
- The intersecting points of two lines is known as a vertex and the lines are the edges/sides.
- Meaning of greek numerals uni, bi, tri ....etc.
- Multimedia resources: Laptop
- Website interactives/ links/ / Geogebra Applets: This geogebra file has been created by Smt Sarah Zakiya Madam, GUHS, Yellagondapalya.
- Process:
- The teacher can tell the students that they are surrounded by many different kinds of shapes every day.
- Many of these shapes are two-dimensional plane figures.
- Plane figures are flat. They can be closed or not closed.
- Plane figures made up of three or more closed line segments are polygons.
- Each line segment of a polygon is a side. Polygons are classified and named based on the number of sides.
- Developmental Questions:
- How many vertices, sides and angles does this figure have ? Name the figure.
- What is the point of intersection of two lines called ?
- What parameters do you identify in each figure ? (side, vertex, angle, plane surface and area )
- What can you say about the number of vertices and the number of sides in each figure ?
- Which figure would you think will be formed if the number of sides is increased indefinately.
- Evaluation:
- What determines the side or edge of the figure ?
- Are the students able to corelate the names with the number of sides ?
- Are the students able to appreciate the nature of shapes formed with each increasing side?
- Students can discuss angle sum property in each case by dividing the figure into triangles or quadrilaterals.
- Question Corner:
- A hexagon is a polygon with _________ angles.
- Is circle a polygon ?
- What is a polygon with 12 sides called ?
- You have a collection of sides from triangles and decagons. The total number of sides is 100 and you have 4 decagons. How many triangles do you have ?
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept #2. Properties and measurements of polygons
Learning objectives
- The sum of the interior angle measures of an n-sided, convex polygon is
- A regular polygon has all sides and angles equal.
- All exterior angles of a polygon add upto 360 degrees.
- Each exterior angle must be
- Each of the exterior angle and interior angles are measured from the same line. hence they add upto 180 degrees.
- Area of Polygon = perimeter × apothem / 2
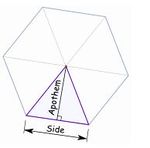
(This image has been taken from:http://www.mathsisfun.com/geometry/regular-polygons.html)
Notes for teachers
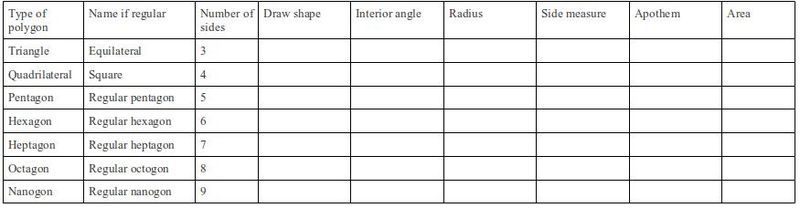
Activity No # 1. Polygon's table of values.
- Estimated Time: 90 minutes.
- Materials/ Resources needed:
- Sheets of paper, scale, compass, protractor, pencil.
- Prerequisites/Instructions, if any:
- Knowledge of different polygons and their names.
- Requisite formulae needed to do the calculations.
- Skills to perform and tabulate calculations accurately.
- Multimedia resources:
- Website interactives/ links/ / Geogebra Applets:
Please refer to this website for more clarity on this activity : http://www.mathsisfun.com/geometry/regular-polygons.html
- Process:
- Use the formulas listed in learning objectives above to make a table of Side, Apothem and Area, compared to a Radius of "1":
- Let the table have the following columns.
- Developmental Questions:
- Name the types of polygons based on their sides.
- What is a regular polygon ?
- How many sides does a ______________ have ?
- What is an interior angle ?
- Is there any relationship between the number of sides and number of angles ?
- What radius has been mentioned here as common for all ?
- What is an apothem ?
- How do you get the central point of a polygon ?
- What is the formula to find the area of a polygon ?
- Evaluation:
- Which measuring parameter do you think is the deciding factor for the area of a polygon ?
- Question Corner
- Can you find the listed measures like interior angle, area without using the formula ? How ? Discuss.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept #3. Types of polygons
Learning objectives
- There are several polygons.
- Polygons are classified by considering their angle measures and side length measures.
- If a polygon's angles and sides are equal, then the polygon is called a regular polygon.
- If the measures of a polygon's angles or side lengths differ, then the polygon is called an irregular polygon.
- Primary shapes can be combined to form composite polygons. (This knowledge will help while deducing area formulae for complex figures which would be derived by splitting them into primary figures.)
Notes for teachers
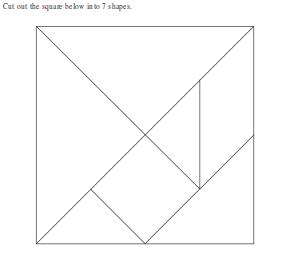
Activity No # Tangram - Building polygons
This activity has been taken from the website :http://www.cimt.plymouth.ac.uk/projects/mepres/allgcse/bs7act1.pdf
- Estimated Time : 40 minutes.
- Materials/ Resources needed: Chart papers, scissors, pencil, scale.
- Prerequisites/Instructions, if any
- An understanding of basic shapes like square, rectangle, parallelogram, triangle and trapezium.
- Ability to draw mentioned shapes accurately and cut exactly on boundaries.
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process:
- This is a very old Chinese puzzle known as a tangram.
- Cut out the square below into 7 shapes.
- Cut out the 7 shapes and rearrange them to form:
(a) a square from two triangles, and then change it to a parallelogram;
(b) a rectangle using three pieces, and then change it into a parallelogram;
(c) a trapezium with three pieces;
(d) a parallelogram with four pieces;
(e) a trapezium from the square, parallelogram and the two small triangles;
(f) a triangle with three pieces;
(g) a rectangle with all seven pieces.
(h) a kite with two traingles.
4. Finally, put the pieces back together to form the original square.
- Developmental Questions:
- Were you all able to read and follow the instructions.
- Name and point the different shapes in the figure.
- Name the dimensions of each shape.
- Evaluation:
- Were the students able to identify the types of polygons based on the number of sides.
- What type of two triangles would you need to form a square ?
- Question Corner:
- What are the characteristic properties of each shape: square, rectangle, triangle, parallelogram and trapezium ?
- What did you learn from this activity ?
Activity No #
- Estimated Time:
- Materials/ Resources needed:
- Prerequisites/Instructions, if any:
- Multimedia resources:
- Website interactives/ links/ / Geogebra Applets:
- Process/ Developmental Questions:
- Evaluation:
- Question Corner:
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Hints for difficult problems
Angle sum property
CLASS IX TOPIC POLYGONS ADDITIONAL PROBLEMS (problem no 3 ) A polygon has 'n' sides .Two of it's angles are right angles and each of remaining angle isFind the value of 'n'. Step 1;(Students must understand the problem) In a polygon of side 'n' two angles are and other angles are each. We must find out value of 'n'. Step 2(Students know the formula for sum of angles of polygon of side 'n') (2n-4)right angles. Step 3(Sum of the angles is equal to what?) There are 'n' angles in a polygon of side 'n'.Out of 'n' angles 2 angles are right anles and other (n-2) angles are each.
(2n-4) = (n-2)<math>\144^0+(2)(90^0)how to open the bracket and substitute the values)
2n x - 4 x =
= (Brings similar terms at one side of the equation)
= (Add and substract and simplify)
=
n = (Devide and simplify)
n = 7
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template