Difference between revisions of "Factorisation"

From Karnataka Open Educational Resources
Jump to navigation Jump to search
 
(19 intermediate revisions by 8 users not shown)
Line 1: Line 1:
 +
<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#ffffff; vertical-align:top; text-align:center; padding:5px;">
 +
''[http://karnatakaeducation.org.in/KOER/index.php/ಅಪವರ್ತಿಸುವಿಕೆ ಕನ್ನಡದಲ್ಲಿ ನೋಡಿ]''</div>
 
<!-- This portal was created using subst:box portal skeleton  -->
 
<!-- This portal was created using subst:box portal skeleton  -->
 
<!--        BANNER ACROSS TOP OF PAGE        -->
 
<!--        BANNER ACROSS TOP OF PAGE        -->
Line 19: Line 21:
 
While creating a resource page, please click here for a resource creation [http://karnatakaeducation.org.in/KOER/en/index.php/Resource_Creation_Checklist '''checklist'''].
 
While creating a resource page, please click here for a resource creation [http://karnatakaeducation.org.in/KOER/en/index.php/Resource_Creation_Checklist '''checklist'''].
 
= Concept Map =
 
= Concept Map =
−
<mm>[[Factorisation of Polynomials.mm|Flash]]</mm>
+
[[File:Factorisation.mm|Flash]]
−
 
 
−
 
 
−
 
 
−
__FORCETOC__
 
  
 
= Textbook =
 
= Textbook =
Line 30: Line 28:
  
 
=Additional Information=
 
=Additional Information=
 +
 +
{{#widget:YouTube|id=LitM6ERl88A}}
 
==Useful websites==
 
==Useful websites==
 +
*Question Corner
 +
 +
 
#[http://www.mathsisfun.com/algebra/polynomials.html Maths is Fun]. This website contains good worksheets for factorisation.
 
#[http://www.mathsisfun.com/algebra/polynomials.html Maths is Fun]. This website contains good worksheets for factorisation.
 
#[http://reference.wolfram.com/mathematica/guide/PolynomialAlgebra.html Wolfram Mathworld].  This website contains good simulations for math identities.
 
#[http://reference.wolfram.com/mathematica/guide/PolynomialAlgebra.html Wolfram Mathworld].  This website contains good simulations for math identities.
Line 45: Line 48:
 
To introduce expressions and the need and method of splitting
 
To introduce expressions and the need and method of splitting
 
===Notes for teachers===
 
===Notes for teachers===
−
===Activity No # ===
+
===Activities===
−
{| style="height:10px; float:right; align:center;"
+
#Activity #1
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
+
#Activity #2 Demonstrate Binomial Cube
−
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
−
|}
 
−
*Estimated Time
 
−
*Materials/ Resources needed
 
−
*Prerequisites/Instructions, if any
 
−
*Multimedia resources
 
−
*Website interactives/ links/ / Geogebra Applets
 
−
*Process/ Developmental Questions
 
−
*Evaluation
 
−
*Question Corner
 
−
 
 
−
===Activity No #2 Demonstrate Binomial Cube===
 
−
{| style="height:10px; float:right; align:center;"
 
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
−
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
−
|}
 
−
*Estimated Time
 
−
*Materials/ Resources needed
 
−
*Prerequisites/Instructions, if any
 
−
*Multimedia resources
 
 
http://www.infomontessori.com/sensorial/montessori_binomial_cube_1.jpg
 
http://www.infomontessori.com/sensorial/montessori_binomial_cube_1.jpg
−
*Website interactives/ links/ / Geogebra Applets
 
−
*Process/ Developmental Questions
 
−
*Evaluation
 
−
*Question Corner
 
  
 
==Concept #==
 
==Concept #==
Line 110: Line 89:
  
  
−
= Hints for difficult problems =
+
# = Hints for difficult problems =
 
Question : If  x= and y= find  
 
Question : If  x= and y= find  
  
Line 134: Line 113:
  
 
Step 8 : =
 
Step 8 : =
 +
#
 +
=hints for difficult problem=
 +
 +
If  x-= 4  prove that <math>x^{3}+6x^{2}+\frac {6}  {x^{2}}-\frac{1}  {x^{3}}=184  </math>
 +
 +
=====If  x+y=a  and xy=b then prove that                                          (1+)+(1+) =
 +
 +
Steps for solution
 +
 +
step 1:  * Understanding the  problem first.
 +
    * Recalling the indentities
 +
 +
step  2 :  * consider the condition and squaring on both side
 +
    * simplify to get the value
 +
 +
step 3:    *  consider  LHS
 +
    *  multiply the expression
 +
    *  substitute the value
 +
    *  simlpify the equqtion
 +
 +
 +
solution for the problem
 +
 +
consider  x+y=a
 +
=
 +
substitute x+y =a and xy=b
 +
then we get
 +
                    ------->(1)
 +
consider xy=b squaring on both side
 +
then we get =------->(2)
 +
 +
consider LHS=
 +
=(1+)+(1+)
 +
=1+
 +
= 1+ from eqn 1 & 2
 +
=
 +
=
 +
        LHS = RHS=============
  
 
= Project Ideas =
 
= Project Ideas =
Line 142: Line 159:
  
 
Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template
 
Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template
 +
 +
[[Category:Class 8]]
 +
[[Category:Algebraic expressions]]

Latest revision as of 16:11, 31 October 2019

ಕನ್ನಡದಲ್ಲಿ ನೋಡಿ

The Story of Mathematics

Philosophy of Mathematics

Teaching of Mathematics

Curriculum and Syllabus

Topics in School Mathematics

Textbooks

Question Bank

While creating a resource page, please click here for a resource creation checklist.

Concept Map

[maximize]

Textbook

To add textbook links, please follow these instructions to: (Click to create the subpage)

Additional Information

Useful websites

  • Question Corner


  1. Maths is Fun. This website contains good worksheets for factorisation.
  2. Wolfram Mathworld. This website contains good simulations for math identities.

Reference Books

NCERT Books

  1. Algebraic expressions and identities
  2. Factorisation

Teaching Outlines

Concept #1 Monomial expressions

Learning objectives

To introduce expressions and the need and method of splitting

Notes for teachers

Activities

  1. Activity #1
  2. Activity #2 Demonstrate Binomial Cube

montessori_binomial_cube_1.jpg

Concept #

Learning objectives

Notes for teachers

Activity No #1 Geogebra

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources

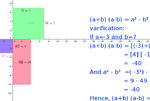
Geogebra screenshot for identities.png
This is a Geogebra screenshot for identity.

This is a classroom demonstration of binomial cube. Show the children before you start the cubic identity.

  • Website interactives/ links/ / Geogebra Applets
  • Process/ Developmental Questions
  • Evaluation
  • Question Corner

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ / Geogebra Applets
  • Process/ Developmental Questions
  • Evaluation
  • Question Corner


  1. = Hints for difficult problems =

Question : If x= and y= find


Solution :

Analysing the given condition

Step 1 : = ()() => Using the formula : = ( )()

step 2 : = ( + )(-) => substitute the value of x and y

Step 3 : = x => take the L.C.M of the denominator , simplyfy using concept of addition and substaction of fraction

Step 4: = x simply the above using basic concepts of addition and substraction

Step 5 : = x 

Step 6 := x => take common term 2 ( H.C.F)

Step 7 : = x

Step 8 : =

hints for difficult problem

If x-= 4 prove that

====If x+y=a and xy=b then prove that (1+)+(1+)

Steps for solution 

step 1:  * Understanding the  problem first.

* Recalling the indentities

step 2 : * consider the condition and squaring on both side * simplify to get the value

step 3: * consider LHS * multiply the expression * substitute the value * simlpify the equqtion


solution for the problem

consider x+y=a = substitute x+y =a and xy=b 

then we get 
                   ------->(1)

consider xy=b squaring on both side then we get =------->(2)

consider LHS= =(1+)+(1+) =1+ = 1+ from eqn 1 & 2 = = 

       LHS = RHS=============

Project Ideas

Math Fun

Usage

Create a new page and type {{subst:Math-Content}} to use this template

Retrieved from "https://karnatakaeducation.org.in/KOER/en/index.php?title=Factorisation&oldid=32253"