Difference between revisions of "Activity1 Pi the mathematical constant"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
===Materials/ Resources needed=== | ===Materials/ Resources needed=== | ||
| − | Digital resources:[https://karnatakaeducation.org.in/KOER/en/images/d/d8/Area_and_Perimeter_of_a_Polygon_inside_the_Circle.ggb Click here to open the | + | Digital resources:[https://karnatakaeducation.org.in/KOER/en/images/d/d8/Area_and_Perimeter_of_a_Polygon_inside_the_Circle.ggb Click here to open the file] |
Non digital resources: Ruler | Non digital resources: Ruler | ||
===Process (How to do the activity)=== | ===Process (How to do the activity)=== | ||
| − | #[https://www.youtube.com/watch?v=_rJdkhlWZVQ&feature=youtu.be Click here for Finding Pi by Archimedes Method]. Archimedes approximated the value of Pi by starting with the fact that a regular hexagon inscribed in a unit circle has a perimeter of 6. He then found a method for finding the perimeter of a polygon with twice as many sides. Applying his method repeatedly, he found the perimeter of a 12, 24, 48, and 96 sided polygon. Using the perimeter as an approximation for the circumference of a circle he was able to derive an approximation for Pi equivalent to 3.14. This video uses a somewhat simpler method of doing the same thing and carries it out to polygons with millions of sides. All that is needed to understand the calculation is knowledge of the Pythagorean Theorem. | + | ##[https://www.youtube.com/watch?v=_rJdkhlWZVQ&feature=youtu.be Click here for Finding Pi by Archimedes Method]. Archimedes approximated the value of Pi by starting with the fact that a regular hexagon inscribed in a unit circle has a perimeter of 6. He then found a method for finding the perimeter of a polygon with twice as many sides. Applying his method repeatedly, he found the perimeter of a 12, 24, 48, and 96 sided polygon. Using the perimeter as an approximation for the circumference of a circle he was able to derive an approximation for Pi equivalent to 3.14. This video uses a somewhat simpler method of doing the same thing and carries it out to polygons with millions of sides. All that is needed to understand the calculation is knowledge of the Pythagorean Theorem. |
| − | # | + | ##{{Geogebra|zvbqkqa7}} |
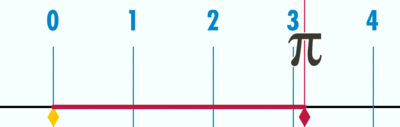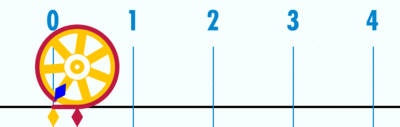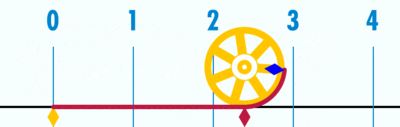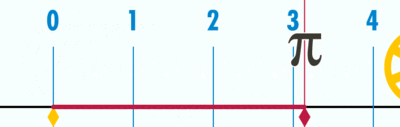
#[http://geogebratube.org/material/show/id/144079 Geogebra file] for explaining how 'circumference / diameter' is a constant, denoted as pi (Greek letter), using a number line | #[http://geogebratube.org/material/show/id/144079 Geogebra file] for explaining how 'circumference / diameter' is a constant, denoted as pi (Greek letter), using a number line | ||
#An animation of the same concept. | #An animation of the same concept. | ||
Revision as of 13:13, 15 July 2020
Objectives
Students will be able to understand the value of Pi is ratio of circle's circumference to its diameter.
Estimated Time
20minutes
Prerequisites/Instructions, prior preparations, if any
Know the concepts of circumference and diameter of a circle.
Materials/ Resources needed
Digital resources:Click here to open the file
Non digital resources: Ruler
Process (How to do the activity)
- Click here for Finding Pi by Archimedes Method. Archimedes approximated the value of Pi by starting with the fact that a regular hexagon inscribed in a unit circle has a perimeter of 6. He then found a method for finding the perimeter of a polygon with twice as many sides. Applying his method repeatedly, he found the perimeter of a 12, 24, 48, and 96 sided polygon. Using the perimeter as an approximation for the circumference of a circle he was able to derive an approximation for Pi equivalent to 3.14. This video uses a somewhat simpler method of doing the same thing and carries it out to polygons with millions of sides. All that is needed to understand the calculation is knowledge of the Pythagorean Theorem.
Download this geogebra file from this link.
- Geogebra file for explaining how 'circumference / diameter' is a constant, denoted as pi (Greek letter), using a number line
- An animation of the same concept.
- Process/ Developmental Questions
Open the Geogebra file. Move the slider to 'unravel' the circumference' over the number line. Since the diameter is 1 unit (measuring from -0.5 to 0.5 on number line), the circumference ends at 3.14, showing the ratio between circumference
- Evaluation
- Question Corner
if the diameter is increased from 1 to 2, what will the circumference be?