Difference between revisions of "Significance of Gravitational Force"

From Karnataka Open Educational Resources
Jump to navigation Jump to search
Line 122: Line 122:
 
Create a new page and type <nowiki>{{subst:Science-Content}}</nowiki> to use this template
 
Create a new page and type <nowiki>{{subst:Science-Content}}</nowiki> to use this template
  
−
= Projectile and Satellite Motion =
 
−
== Concept flow ==
 
−
 
−
*A projectile motion of a body thrown is due to the gravitational force.
 
−
 
−
*Satellites are projectiles that are continuously falling in the orbit around planets
 
−
 
−
 
−
Let us study this picture below and analyze what happens in each of the cases.
 
−
 
−
 
−
[[Image:Gravitation%20for%20wiki_html_545339b5.gif]] <br>
 
−
 
−
In the first case, the ball is just dropped from the cliff and it falls down in a straight line, subject to the force of gravity. In the second and third instances, the ball is thrown upwards, reaches a certain height and still falls down. In the third case, the ball covers a horizontal range as well.
 
−
 
−
In all these cases, gravity is the only force acting. Without gravity, we could throw a rock upwards at an angle and it follow a straight line path. Because of gravity, however, the path curves.
 
−
 
−
Such an object, when thrown/ projected and continues its motion on its own inertia is called a projectile. A projectile will have two components to ots velocity – the horizontal and the vertical. The horizontal component is similar to an object rolling on a plane/ along a straight line. The vertical component of the velocity is subject to the acceleration due to gravity. A projectile moves horizontally as it moves downwards or upwards.
 
−
 
−
Imagine throwing a ball straight up. It will fall down to the same place. In this case the ball has a velocity in the vertical direction which changes with time as the force due to gravity causes an acceleration in the downward direction all the time. But suppose on were to throw a ball with only a horizontal velocity. The ball will now move with a velocity that has two components to it - one the horizontal velocity which remains unchanged as long as there is no force such as air resistance acting on it and a vertical velocity that is continually changing. This vertical velocity starts at zero - we threw the ball horizontally - and keeps increasing with an acceleration g.
 
−
 
−
The resultant velocity is a combination of the two. This is what causes objects to follow a parabolic path when they are thrown with a combination of horizontal and vertical velocities.
 
−
The greater the horizontal component the farther the ball will travel. For short distances, and small velocities, the curvature of the Earth will make no difference.
 
−
But suppose that we throw it so hard that the horizontal distance is very large and we can no longer ignore the curvature of the Earth?
 
−
 
−
Suppose we throw it so hard that that ball will continue to fall but will never reach the ground - the curvature of the fall of the ball is greater than the curvature of the Earth? Then the ball will become a satellite! It will move round and round the Earth - constantly falling but never reaching the ground!
 
−
 
−
The satellite and everything in it are constantly falling towards the Earth but will never reach it. Since they are all falling with the same velocity, the satellite does not exert any force on the objects or people inside. The people inside, therefore feel weightless. remember we have a sense of weight because of the Normal force. Here the Normal force is zero and so we feel weightless.
 
−
 
−
This is very similar to the sense of loss of weight in a lift that is accelerating downwards - except that here the acceleration is the acceleration due to gravity.<br><br>
 
 
== Satellite ==
 
== Satellite ==
  

Revision as of 10:18, 4 December 2013

The Story of Science

Philosophy of Science

Teaching of Science

Curriculum and Syllabus

Topics in School Science

Textbooks

Question Bank

While creating a resource page, please click here for a resource creation checklist

Concept Map

Error: Mind Map file Significance_of_gravitational_force.mm not found



Textbook

To add textbook links, please follow these instructions to: (Click to create the subpage)

Additional information

Useful websites

Reference Books

Teaching Outlines

Significance of the gravitational force =

Discovery of planets ==

Accurate measurements on the orbits of the plantes indicated that they did not precisely follow Kepler's laws. Slight deviations from perfectly elliptical orbits were observed. Newton was aware that this was to be expected from the Law of Universal Gravitation. The derivation of perfectly elliptical ignores the forces due to the other planets. These deviations called perturbations are observed and led to the discovery of Neptune and Pluto. Planets around distant stars were also inferred from the regular wobble of each star due to the gravitational attraction of the revolving plant.

Ocean tides ==

Ocean tides are caused by differences in the gravitational pull between the Moon and the Earth on the opposite sides of the Earth. Gravitational force is stronger on the side of the Earth nearer to the Moon and is weaker on the side of the Earth farther from the Moon. The bulge that is caused in the Earth's oceans due to this gravitational pull results in two sets of tides on the Earth.

Concept #1 - Projectile and Satellite Motion

Learning objectives

Notes for teachers

These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ simulations
  • Process (How to do the activity)
  • Developmental Questions (What discussion questions)
  • Evaluation (Questions for assessment of the child)
  • Question Corner

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ simulations
  • Process (How to do the activity)
  • Developmental Questions (What discussion questions)
  • Evaluation (Questions for assessment of the child)
  • Question Corner


Concept #

Learning objectives

Notes for teachers

These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ simulations
  • Process (How to do the activity)
  • Developmental Questions (What discussion questions)
  • Evaluation (Questions for assessment of the child)
  • Question Corner


Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ simulations
  • Process (How to do the activity)
  • Developmental Questions (What discussion questions)
  • Evaluation (Questions for assessment of the child)
  • Question Corner

Project Ideas

Fun corner

Usage

Create a new page and type {{subst:Science-Content}} to use this template

Satellite

An Earth satellite is simply a projectile that falls around the Earth rather than into it. That means the horizontal falling distance matches the Earths curvature. Geometrically, the curvature of the surface is that its surface drops a vertical distance of 5 metres for every 8000 metres tangent to the surface.

Therefore, if we throw a rock or a ball at a high enough speed (about 29000 km/s), it would follow the curvature of the Earth. But at this speed, atmospheric friction (due to air drag) would burn up everything. This is why satellites are launched at an altitude high enough for the air drag to be negligible.

Satellite motion was understood by Newton who reasoned that the Moon was simply a projectile that was circling the Earth.

Activity 4 - Demonstration of satellite motion using simulation

The following simulation can illustrate how satellite motion takes place.


Click to run PhET simulation

Kepler's Laws

Concept flow

  • The key concept to understand here is that gravitational forces play an important role in planetary motion.
  • Three laws of planetary motion that describe the motion of the planets have been postulated based on detailed astronomical observations

Laws of Planetary Motion

We now know that satellites are continually falling towards the Earth following a curved path whose curvature is greater than that of the curvature of the Earth. The Moon is just such a satellite that moves around the Earth. In a similar way, all the planets that move around the Sun are satellites of the Sun. The motion described in such a situation is not strictly circular - it is elliptical.

Johannes Kepler, working with data painstakingly collected by Tycho Brahe without the aid of a telescope, developed three laws which described the motion of the planets across the sky.

1. The Law of Orbits: All planets move in elliptical orbits, with the sun at one focus.

2. The Law of Areas: Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal periods of time.

3. The Law of Periods: The square of the period of any planet is proportional to the cube of the semimajor axis of its orbit.

Kepler's laws were derived for orbits around the sun, but they apply to satellite orbits as well.

The Law of Orbits

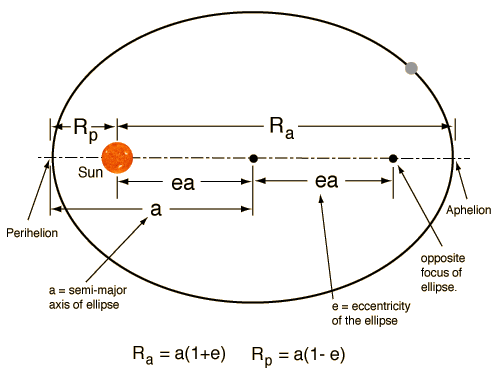
All planets move in elliptical orbits, with the sun at one focus. An ellipse is a closed curve such that the sum of the distances from any point P on the curve to two fixed points (called the foci, F1 and F2) remains constant.

Orbit eccentricity

The semi major axis of the ellipse is a and represents the planet's average distance from the Sun. The eccentricity, “e” is defined so that “ea” is the distance from the centre to either focus. A circle is a special case of an ellipse where the two foci coincide. The Earth and most of the other planets have nearly circular orbits. For Earth, “e” = 0.017.


Gravitation for wiki html m75870f64.gif

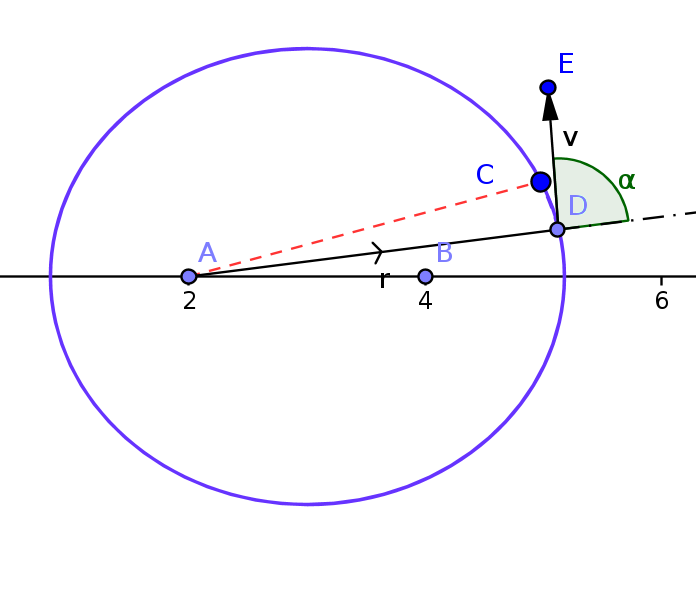
The Law of Equal Areas

Kepler's second law states that each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal periods of time.

This can be shown to be true using the law of conservation of angular momentum.

Gravitation for wiki html m4a5ede30.png

If “v” is the velocity of the planet, in time “dt” the planet moves a distance vdt and sweeps out an area equal to the area of a triangle of base “r” and altitude vdt sinα.

Hence dA = ½ (r) (“v” x “dt” x sinα)

dA/ dt = ½ rv sinα

The magnitude of the angular momentum of the planet about the Sun is L = mvr sinα.

dA/ dt = (½)L/m

Because the angular momentum is conserved, the rate of change of area covered is constant. This means that the planets move with different velocities depending upon their position in the orbits.

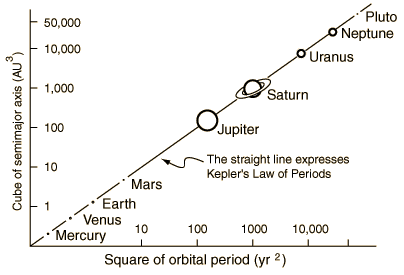
The Law of Periods

The ratio of the squares of the periods of any two planets revolving about the Sun is equal to the ratio of the cubes of their semi-major axes.

Can you derive this?

Gravitation for wiki html m290004f7.gif

G m1 Ms / r12 = m1 (v12)/ r1

v1 = 2πr1/T1

Substituting and rearranging we get

T12/ r13 = 4π2 / G Ms

Deriving this for another planet, we can arrive at the third law.

5. www.hyperphysics.com - From Classical Mechanics to General Relativity - This is a good description of the geometry of Newtonian gravity and how to move from classical mechanics to relativity.


8. http://www.physicsclassroom.com/Class/circles/U6L4b.cfm -This website describes the mathematics of orbital motion.

9. http://spaceflight.nasa.gov/gallery/images/station/crew-9/html/iss008e21996.html

Keywords

Mass, Inertial, Gravitational, Force field, Universal law of gravitation, Acceleration due to gravity, “g”, weight, weightlessness

Retrieved from "https://karnatakaeducation.org.in/KOER/en/index.php?title=Significance_of_Gravitational_Force&oldid=7245"