Difference between revisions of "Formation of a triangle"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
*Recognize elements of triangle | *Recognize elements of triangle | ||
*Introduce concepts of exterior angle. | *Introduce concepts of exterior angle. | ||
| − | [[File:Triangle formation.png|thumb|600x600px|'''[https:// | + | [[File:Triangle formation.png|thumb|600x600px|'''[https://ggbm.at/z4h42k8z Introduction to a triangle.ggb]''']] |
===Estimated Time=== | ===Estimated Time=== | ||
Revision as of 15:56, 12 April 2019
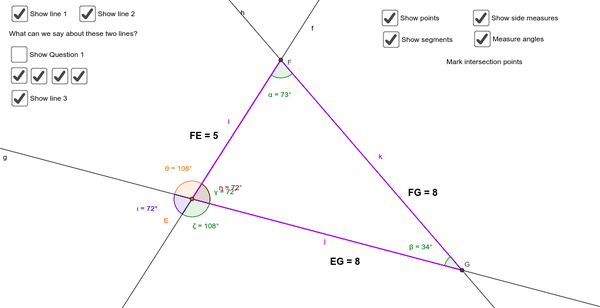
Three lines intersect with each other in a plane to form a closed figure. Vertices are formed at the intersecting points and edges that mark the triangle are sides.
Objectives
- Understand formation of triangles
- Recognize elements of triangle
- Introduce concepts of exterior angle.
Estimated Time
30 minutes
Prerequisites/Instructions, prior preparations, if any
Prior knowledge of point, lines, angles, parallel lines
Materials/ Resources needed
- Digital : Computer, geogebra application, projector.
- Non digital : Worksheet and pencil
- Geogebra files : “Introduction to a triangle.ggb”
Process (How to do the activity)
- Use the geogebra file to illustrate. The questions below will are used to interact with the geogebra sketch.
- How many lines are there? Are the lines meeting?
- Are the two lines parallel? How can you say they are parallel or not?
- How many angles are formed at the point of intersection?
- What is the measure of the total angle at the point of intersection of two lines?
- Of the four angles formed which of the angles are equal? What are they called?
- Do the three intersecting lines enclose a space? How does it look? It is called a triangle.
- What are the points of intersection of these three lines called?
- The line segments forming the triangle are called sides.
- How many angles are formed when three lines intersect with each other?
- How many angles are enclosed by the triangle?
Evaluation at the end of the activity
- Can there be a closed figure with less than three sides?
- Can the vertices of the triangle be anywhere on a plane?
- What will happen if the three vertices are collinear?