Difference between revisions of "Triangles"
suchethass (talk | contribs) |
suchethass (talk | contribs) |
||
| Line 168: | Line 168: | ||
Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template | Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 07:19, 6 December 2013
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Error: Mind Map file 5._Triangles.mm not found
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Useful websites
This is a reference website for types and classification off triangles
Reference Books
Teaching Outlines
Concept #1 What is a triangle
Learning objectives
- Triangle is a polygon
- Sides and angles determine the type of triangle
- The relationship between sides and angles of triangle
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Triangle is the most basic polygon shape. Triangles are classified on the basis of their angles and sides.
Click here for notes on types of triangles.
Activity No #1 - Make your triangle
- Estimated Time - 40 minutes
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ Geogebra Applets
- Process (How to do the activity)
Mark three non-collinear point P, Q and R on a paper. Join these points in all possible ways. The segments are PQ, QR and RP. A simple close curve formed by these three segments is called a triangle. It is named in one of the following ways.
Triangle PQR or Triangle PRQ or Triangle QRP or Triangle RPQ or Triangle RQP .
- Developmental Questions (What discussion questions)
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. In fact, it is the polygon with the least number of sides.
A triangle PQR consists of all the points on the line segment PQ,QR and RP. The three line segments, PQ, QR and RP that form the triangle PQ, are called the sides of the triangle PQR.
How many angles? A triangle has three angles. In figure, the three angles are ∠PQR ∠QRP and ∠RPQ A triangle has six parts, namely, three sides,PQ QRand RP.Three angles ∠PQR ∠QRP and ∠RPQ. These are also known as the elements of a triangle.
What are the intersection points of line segments? The point of intersection of the sides of a triangle is known as its vertex. In figure, the three vertices are P, Q and R. In a triangle, an angle is formed at the vertex. Since it has three vertices, so three angles are formed. The word triangle =tri + angle ‘tri’ means three. So, triangle means closed figure of straight lines having three angles.
- Evaluation (Questions for assessment of the child)
- Question Corner
Activity No # 2 - Types of triangles - Identifying and naming
Part 1
- Estimated time - 20 minutes
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ Geogebra Applets
- Process (How to do the activity)
Identify and name the triangles in the above figure.
- Evaluation
- Is it possible to construct a triangle with 3 collinear points?
- Is it possible to construct a triangle whose sides are 3cm, 4cm and 9cm. Why?.
Part 2
- Estimated time - 20 minutes
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
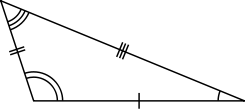
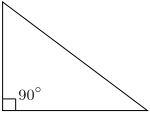
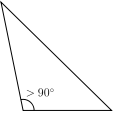
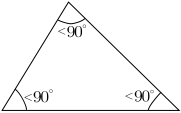
Look at the following images below
|
|
|
|
|
|
- Website interactives/ links/ Geogebra Applets
- Process (How to do the activity)
Identify and name the triangles in the above figure.
- Evaluation
- Can a scalene triangle also be a right-angled triangle ? If yes can you draw one ?
Concept #
Learning objectives
Notes for teachers
These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ Geogebra Applets
- Process (How to do the activity)
- Developmental Questions (What discussion questions)
- Evaluation (Questions for assessment of the child)
- Question Corner
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ Geogebra Applets
- Process (How to do the activity)
- Developmental Questions (What discussion questions)
- Evaluation (Questions for assessment of the child)
- Question Corner
Hints for difficult problems
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template