Revision as of 07:50, 6 December 2013

While creating a resource page, please click here for a resource creation checklist.

Concept Map

Error: Mind Map file 5a._Similar_and_Congruent_triangles.mm not found

Textbook

To add textbook links, please follow these instructions to: (Click to create the subpage)

Additional Information

Useful websites

Reference Books

Teaching Outlines

Concept #1 - Understanding similarity

Learning objectives

To show similar planar figures, discuss congruence and properties of congruent/ similar triangles

Notes for teachers

These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.

Activity No #1 Identifying similar shapes, similar triangles

Click to Comment

Estimated Time - 80 minutes (40 +40)
Materials/ Resources needed - Blackboard, Geogebra files + projector, Calculator
Prerequisites/Instructions, if any
Multimedia resources
Website interactives/ links/ Geogebra Applets
Process (How to do the activity)

Draw figures on the boards - planar figures and triangles
Draw pairs of figures on the board [ both similar and dissimilar]; they can identify overlap of congruent figures
Demonstrate using Geogebra files and discuss

Developmental Questions (What discussion questions)

Can you identify similar figures?
If the children know the names of the theorem, can they explain SSS, AAA, ASA?
What does a ratio of side mean? What is proportionality?
In the Geogebra files, when I change the sides/ proportion, the triangles change in size. But the proportion remains the same, angle remains the same
With calculator verify the proportion (this is very very useful for involving the whole class) they all can see the proportion remains constant though the size changes
Show the arithmetic behind the proportion
Note - When there is a wrong answer, identify what is the source of the confusion – sides, ratio and proportion

Evaluation (Questions for assessment of the child)

Distinguish congruence and similarity
Can they relate the theorem to the facts and figures?

Question Corner

Activity No #

Click to Comment

Estimated Time
Materials/ Resources needed
Prerequisites/Instructions, if any
Multimedia resources
Website interactives/ links/ Geogebra Applets
Process (How to do the activity)
Developmental Questions (What discussion questions)
Evaluation (Questions for assessment of the child)
Question Corner

Concept #

Learning objectives

Notes for teachers

These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.

Activity No #

Click to Comment

Estimated Time
Materials/ Resources needed
Prerequisites/Instructions, if any
Multimedia resources
Website interactives/ links/ Geogebra Applets
Process (How to do the activity)
Developmental Questions (What discussion questions)
Evaluation (Questions for assessment of the child)
Question Corner

Activity No #

Click to Comment

Estimated Time
Materials/ Resources needed
Prerequisites/Instructions, if any
Multimedia resources

Suchetha . S. S Asst. Teacher ( Mathematics ) GJC Thyamagondlu. Nelamangala Talluk Bangalore Rural District doing the activity below on a lesson on similar triangles using GeoGebra in the classroom

Website interactives/ links/ Geogebra Applets
Process (How to do the activity)
Developmental Questions (What discussion questions)
Evaluation (Questions for assessment of the child)
Question Corner

Hints for difficult problems

Project Ideas

Math Fun

Usage

Create a new page and type {{subst:Math-Content}} to use this template

Pythagorean Theorem

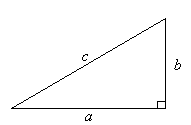
Pythagoras' Theorem was discovered by Pythagoras, a Greek mathematician and philosopher who lived between approximately 569 BC and 500 BC.

Pythagoras' Theorem states that:

In any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. That is:

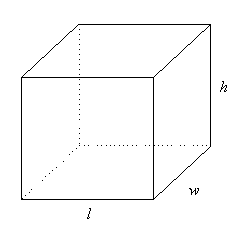
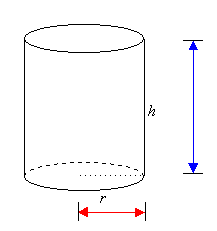
Pythagoras' Theorem in Three Dimensions

A three-dimensional object can be described by three measurements - length, width and height.

We can use Pythagoras' Theorem to find the length of the longest straw that will fit inside

the box or cylinder.

GeoGebra Contributions

The GeoGebra file below to understand Similar Triangles
1. Similar Triangles Part 1 http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_1.html
2. Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_1.ggb
3. Similar Triangles Part 2 http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_2.html
4. Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_2.ggb
5. Similar Triangles Part 3 http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_3.html
6. Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/Similar_Triangles_3.ggb
7. See a video to understand this concept http://www.youtube.com/watch?v=BI-rtfZVXy0

The GeoGebra file below verifies the Thales theorem
1. Thales Theorem http://www.karnatakaeducation.org.in/KOER/Maths/thales_theorem.html
2. Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/thales_theorem.ggb
3. See a video that proves this theorem http://www.youtube.com/watch?v=Y-6yYsuGLoc

@@ Line 39: / Line 39: @@
 ''These are short notes that the teacher wants to share about the concept, any locally relevant information, specific instructions on what kind of methodology used and common misconceptions/mistakes.''
-===Activity No #1 ===
+===Activity No #1 Identifying similar shapes, similar triangles===
 {| style="height:10px; float:right; align:center;"
 |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 ''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 |}
+* '''Estimated Time''' - 80 minutes (40 +40)
+* '''Materials/ Resources needed''' - Blackboard, Geogebra files + projector, Calculator
-==== Material and Resources Required ====
-Blackboard
-Geogebra files +
-projector
-Calculator
-'''[[Pre-requisites/Instructions]] '''
-* Planar figures and 	triangles
-* Draw pairs of 	figures on the board [ both similar and dissimilar]; they can 	identify overlap of congruent figures
-* Ask the children 	to identify
-* If the children 	know the names of the theorem, ask them to explain- ask them what is 	SSS, AAA, ASA
-* Show ratio and 	give the idea of proportionality
-* Geogebra files. 	When I change the sides/ proportion, the triangles change in size. 	But the proportion remains the same, angle remains the same
-* With calculator 	they verify proportion (this is very very useful for involving the 	whole class) they all can see the proportion remains constant though 	the size changes
-* Show the 	arithmetic behind the proportion
-==== Evaluation ====
-[Activity evaluation -
-What should the teacher watch for when you do the activity; based on
-what they know change]
-* Confusion between 	congruence and similarity
-* When they give the 	theorem, if they cannot identify included side and angle
-* When there is a 	wrong answer, identify what is the source of the confusion – 	sides, ratio and proportion
-* Direct 	substitution
-* '''Estimated Time'''
-* '''Materials/ Resources needed'''
 * '''Prerequisites/Instructions, if any'''
 * '''Multimedia resources'''
 * '''Website interactives/ links/ Geogebra Applets'''
 * '''Process (How to do the activity)'''
+#Draw figures on the boards - planar figures and triangles
+#Draw pairs of figures on the board [ both similar and dissimilar]; they can identify overlap of congruent figures
+#Demonstrate using Geogebra files and discuss
 * '''Developmental Questions (What discussion questions)'''
+# Can you identify similar figures?
+# If the children know the names of the theorem, can they explain SSS, AAA, ASA?
+# What does a ratio of side mean? What is proportionality?
+# In the Geogebra files, when I change the sides/ proportion, the triangles change in size. But the proportion remains the same, angle remains the same
+#With calculator  verify the proportion (this is very very useful for involving the whole class) they all can see the proportion remains constant though the size changes
+#Show the arithmetic behind the proportion
+# Note - When there is a wrong answer, identify what is the source of the confusion – 	sides, ratio and proportion
 * '''Evaluation (Questions for assessment of the child)'''
+#Distinguish congruence and similarity
+#Can they relate the theorem to the facts and figures?
 * '''Question Corner'''
 ===Activity No # ===
 {| style="height:10px; float:right; align:center;"
@@ Line 147: / Line 113: @@
 * '''Prerequisites/Instructions, if any'''
 * '''Multimedia resources'''
+[[Image:KOER%20Triangles_html_m3d25043b.jpg|400px|left]]Suchetha . S. S  Asst. Teacher ( Mathematics ) GJC Thyamagondlu. Nelamangala Talluk Bangalore Rural District doing the activity below on a lesson on similar triangles using GeoGebra in the classroom
 * '''Website interactives/ links/ Geogebra Applets'''
 * '''Process (How to do the activity)'''
@@ Line 163: / Line 130: @@
 Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template
-== Evaluation ==
-== Self-Evaluation ==
-== Further Explorations ==
-== Enrichment Activities ==
 = Pythagorean Theorem =
@@ Line 217: / Line 176: @@
-== Evaluation ==
-== Self-Evaluation ==
-== Further    Explorations ==
-== Enrichment    Activities ==
-= See    Also =
-= Teachers    Corner =
-Suchetha . S. S  Asst. Teacher ( Mathematics ) GJC Thyamagondlu. Nelamangala Talluk Bangalore Rural District doing a lesson on similar triangles using GeoGebra in the classroom
-[[Image:KOER%20Triangles_html_m3d25043b.jpg|600px]]
 == GeoGebra Contributions ==
 # The GeoGebra file below to understand Similar Triangles <br>
@@ Line 256: / Line 190: @@
 ## Download ggb file here http://www.karnatakaeducation.org.in/KOER/Maths/thales_theorem.ggb
 ## See a video that proves this theorem http://www.youtube.com/watch?v=Y-6yYsuGLoc
-= Books =
-= References =
-== Enrichment    Activities ==
-=== Activity 2 Similar Triangles ===
-'''Learning Objective'''
-To show similar planar
-figures, discuss congruence and properties of congruent/ similar
-triangles
-==== Material and Resources Required ====
-Blackboard
-Geogebra files +
-projector
-Calculator
-'''[[Pre-requisites/Instructions]] '''
-* Planar figures and 	triangles
-* Draw pairs of 	figures on the board [ both similar and dissimilar]; they can 	identify overlap of congruent figures
-* Ask the children 	to identify
-* If the children 	know the names of the theorem, ask them to explain- ask them what is 	SSS, AAA, ASA
-* Show ratio and 	give the idea of proportionality
-* Geogebra files. 	When I change the sides/ proportion, the triangles change in size. 	But the proportion remains the same, angle remains the same
-* With calculator 	they verify proportion (this is very very useful for involving the 	whole class) they all can see the proportion remains constant though 	the size changes
-* Show the 	arithmetic behind the proportion
-==== Evaluation ====
-[Activity evaluation -
-What should the teacher watch for when you do the activity; based on
-what they know change]
-* Confusion between 	congruence and similarity
-* When they give the 	theorem, if they cannot identify included side and angle
-* When there is a 	wrong answer, identify what is the source of the confusion – 	sides, ratio and proportion
-* Direct 	substitution

Difference between revisions of "Similarity and Congruence"

Revision as of 07:50, 6 December 2013

Contents

Concept Map

Textbook

Additional Information

Useful websites

Reference Books

Teaching Outlines

Concept #1 - Understanding similarity

Learning objectives

Notes for teachers

Activity No #1 Identifying similar shapes, similar triangles

Activity No #

Concept #

Learning objectives

Notes for teachers

Activity No #

Activity No #

Hints for difficult problems

Project Ideas

Math Fun

Pythagorean Theorem

GeoGebra Contributions

Navigation menu

Search