Difference between revisions of "Statistics"
| Line 1: | Line 1: | ||
| − | + | ||
| − | + | ||
| − | + | ||
| Line 7: | Line 7: | ||
| − | + | ||
| − | + | ||
| Line 71: | Line 71: | ||
=== Descriptive and Inferential Statistics === | === Descriptive and Inferential Statistics === | ||
| − | + | ||
| − | + | ||
| Line 176: | Line 176: | ||
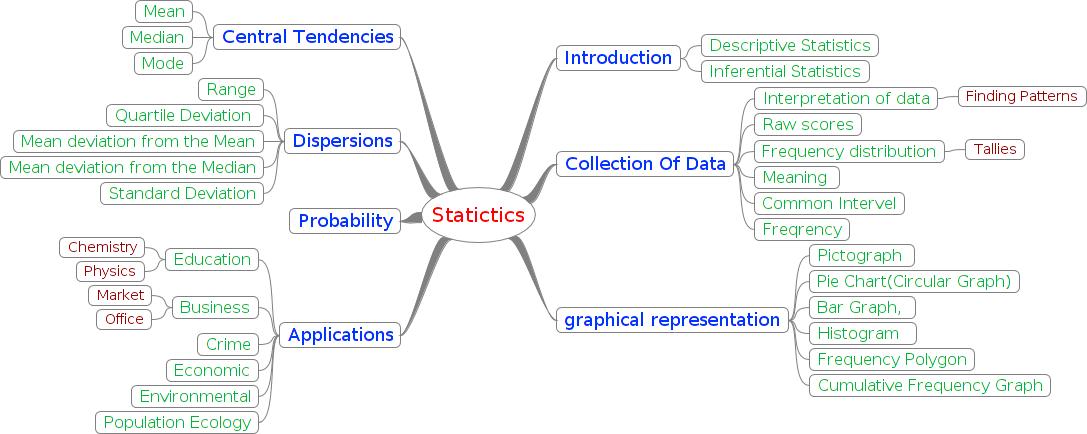
= Mind Map = | = Mind Map = | ||
| − | + | ||
| − | [[Image:KOER-%20Mathematics%20-%20Statistics_html_m14464871.jpg]] | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_m14464871.jpg]] |
| Line 230: | Line 230: | ||
written as numbers, for example, if you were collecting data from | written as numbers, for example, if you were collecting data from | ||
people on their height or weight. | people on their height or weight. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| Line 247: | Line 271: | ||
| − | + | ||
| Line 255: | Line 279: | ||
| − | + | ||
| Line 274: | Line 298: | ||
* A teacher may ask “How many hours of TV by students on TV' to get an idea of what children are learning from TV at home and how it supplements (or affects) the learning in the school | * A teacher may ask “How many hours of TV by students on TV' to get an idea of what children are learning from TV at home and how it supplements (or affects) the learning in the school | ||
| − | + | ||
| Line 312: | Line 336: | ||
# Specialised equipment (rainwater gauges to measure rainfall in a place, various medical equipment that collect information about different biological processes) | # Specialised equipment (rainwater gauges to measure rainfall in a place, various medical equipment that collect information about different biological processes) | ||
| − | + | ||
| Line 321: | Line 345: | ||
| − | + | ||
| Line 331: | Line 355: | ||
| − | + | ||
NatWest One Day | NatWest One Day | ||
| − | International Series: England v India | + | International Series: England v India |
Friday, 16 September 2011 at | Friday, 16 September 2011 at | ||
The Swalec Stadium | The Swalec Stadium | ||
| Line 362: | Line 386: | ||
|} | |} | ||
| − | + | ||
| Line 372: | Line 396: | ||
|- | |- | ||
| | | | ||
| − | + | Name | |
| | | | ||
| − | + | Wicket | |
| Line 459: | Line 483: | ||
| | | | ||
| − | + | ||
| Line 550: | Line 574: | ||
| | | | ||
| − | + | - | |
| Line 608: | Line 632: | ||
| | | | ||
| − | + | - | |
| Line 633: | Line 657: | ||
| | | | ||
| − | + | - | |
| Line 645: | Line 669: | ||
| | | | ||
| − | + | - | |
| Line 654: | Line 678: | ||
| | | | ||
| − | + | - | |
| Line 670: | Line 694: | ||
|} | |} | ||
| − | + | ||
| Line 825: | Line 849: | ||
|} | |} | ||
| − | + | ||
|} | |} | ||
| − | + | ||
| Line 840: | Line 864: | ||
and wrote the choice of fruit against each name. This list would help | and wrote the choice of fruit against each name. This list would help | ||
the teacher to distribute fruits according to the choice. | the teacher to distribute fruits according to the choice. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 911: | Line 931: | ||
|} | |} | ||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| Line 924: | Line 940: | ||
this information to Maria. Maria does so using a paper and a pencil. | this information to Maria. Maria does so using a paper and a pencil. | ||
After arranging the choices in a column, she puts against a choice of | After arranging the choices in a column, she puts against a choice of | ||
| − | food one ( | + | food one ( / ) mark for every student making that choice. |
| + | |||
| + | |||
| + | |||
| Line 949: | Line 968: | ||
| | | | ||
| − | + | /////////////// // | |
| − | + | ///////////// | |
| − | + | //////////////////// | |
|} | |} | ||
| − | + | ||
| − | + | ||
Umesh, after seeing the | Umesh, after seeing the | ||
table suggested a better method to count the students. He asked | table suggested a better method to count the students. He asked | ||
| − | Maria to organise the marks ( | + | Maria to organise the marks ( / ) in a group of ten as shown below : |
| Line 994: | Line 1,013: | ||
| | | | ||
| − | + | ////////// /////// | |
| − | + | ////////// /// | |
| − | + | ////////// ////////// | |
| Line 1,014: | Line 1,033: | ||
|} | |} | ||
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| Line 1,050: | Line 1,075: | ||
| | | | ||
| − | + | ///// ///// ///// | |
| − | + | // | |
| − | + | ///// ///// /// | |
| − | |||
| − | + | ///// ///// ///// ///// | |
| Line 1,072: | Line 1,096: | ||
|} | |} | ||
| − | + | ||
| − | + | ||
| Line 1,086: | Line 1,110: | ||
| − | + | ||
| Line 1,109: | Line 1,133: | ||
| | | | ||
| − | + | ///// // | |
| Line 1,122: | Line 1,146: | ||
| | | | ||
| − | + | ///// | |
| Line 1,135: | Line 1,159: | ||
| | | | ||
| − | + | ///// / | |
| Line 1,148: | Line 1,172: | ||
| | | | ||
| − | + | //// | |
| Line 1,156: | Line 1,180: | ||
|} | |} | ||
| − | + | ||
| Line 1,178: | Line 1,202: | ||
| − | + | ||
| Line 1,186: | Line 1,210: | ||
| − | + | ||
| Line 1,256: | Line 1,280: | ||
|} | |} | ||
| − | + | ||
| Line 1,305: | Line 1,329: | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|- | |- | ||
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
| | | | ||
| − | + | - | |
|} | |} | ||
| − | + | ||
| − | + | ||
| Line 1,704: | Line 1,728: | ||
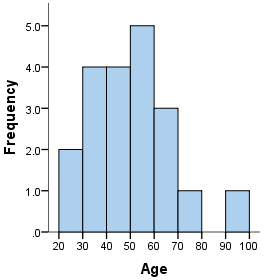
=== What is a histogram? === | === What is a histogram? === | ||
| − | + | ||
| Line 1,715: | Line 1,739: | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[Image:KOER-%20Mathematics%20-%20Statistics_html_6201ec25.png]] | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_6201ec25.png]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| Line 1,789: | Line 1,813: | ||
| − | + | ||
=== How do you construct a histogram from a continuous variable? === | === How do you construct a histogram from a continuous variable? === | ||
| − | + | ||
| Line 1,807: | Line 1,831: | ||
| − | + | ||
| Line 1,838: | Line 1,862: | ||
| − | + | ||
| Line 1,850: | Line 1,874: | ||
| − | + | ||
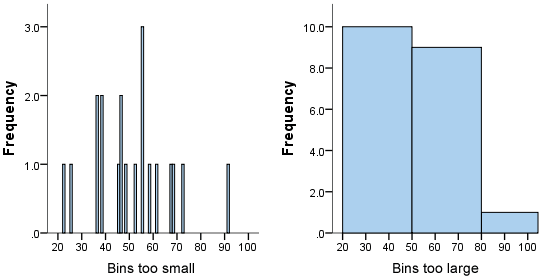
=== Choosing the correct bin width === | === Choosing the correct bin width === | ||
| − | + | ||
| Line 1,866: | Line 1,890: | ||
| − | + | ||
| − | [[Image:KOER-%20Mathematics%20-%20Statistics_html_75ab55c3.png]] | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_75ab55c3.png]] |
| − | + | ||
| − | + | ||
| Line 1,891: | Line 1,915: | ||
| − | + | ||
| Line 1,907: | Line 1,931: | ||
| − | + | ||
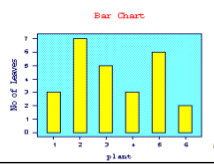
=== What is the difference between a bar chart and a histogram? === | === What is the difference between a bar chart and a histogram? === | ||
| − | [[Image:KOER-%20Mathematics%20-%20Statistics_html_6dfca87b.png]] | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_6dfca87b.png]] |
| Line 1,923: | Line 1,947: | ||
| − | + | ||
| − | + | ||
| − | + | ||
| Line 1,941: | Line 1,965: | ||
| − | + | ||
| Line 1,951: | Line 1,975: | ||
| − | + | ||
| Line 1,978: | Line 2,002: | ||
| − | + | ||
| − | + | ||
| Line 2,108: | Line 2,132: | ||
|} | |} | ||
| − | + | ||
| − | + | ||
| Line 2,124: | Line 2,148: | ||
| − | + | ||
| Line 2,254: | Line 2,278: | ||
=== Dependent and Independent Variables === | === Dependent and Independent Variables === | ||
| − | + | ||
| − | + | ||
| Line 2,264: | Line 2,288: | ||
| − | + | ||
| − | + | ||
| Line 2,279: | Line 2,303: | ||
| − | + | ||
| − | + | ||
| Line 2,287: | Line 2,311: | ||
| − | + | ||
| − | + | ||
| Line 2,295: | Line 2,319: | ||
| − | + | ||
| − | + | ||
| Line 2,312: | Line 2,336: | ||
| − | + | ||
| − | + | ||
| Line 2,325: | Line 2,349: | ||
| − | + | ||
| − | + | ||
| Line 2,336: | Line 2,360: | ||
=== Experimental and Non-Experimental Research === | === Experimental and Non-Experimental Research === | ||
| − | + | ||
| − | + | ||
| Line 2,378: | Line 2,402: | ||
| − | + | ||
| − | + | ||
=== Categorical and Continuous Variables === | === Categorical and Continuous Variables === | ||
| − | + | ||
| − | + | ||
| Line 2,393: | Line 2,417: | ||
| − | + | ||
| − | + | ||
| Line 2,437: | Line 2,461: | ||
| − | + | ||
| − | + | ||
| Line 2,446: | Line 2,470: | ||
| − | + | ||
| − | + | ||
| Line 2,471: | Line 2,495: | ||
| − | + | ||
| − | + | ||
=== Ambiguities in classifying a type of variable === | === Ambiguities in classifying a type of variable === | ||
| − | + | ||
| − | + | ||
| Line 2,492: | Line 2,516: | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 2,550: | Line 2,567: | ||
| − | + | ||
| − | + | ||
| Line 2,593: | Line 2,610: | ||
| − | + | ||
| − | + | ||
| Line 2,731: | Line 2,748: | ||
| − | + | ||
| − | + | ||
| Line 2,782: | Line 2,799: | ||
|} | |} | ||
| − | + | ||
| − | + | ||
| Line 2,790: | Line 2,807: | ||
| − | + | ||
| − | + | ||
| Line 2,841: | Line 2,858: | ||
|} | |} | ||
| − | + | ||
| − | + | ||
| Line 2,854: | Line 2,871: | ||
| − | + | ||
| − | + | ||
| Line 2,901: | Line 2,918: | ||
|} | |} | ||
| − | + | ||
| − | + | ||
We again rearrange that data into order of | We again rearrange that data into order of | ||
| − | magnitude (smallest first): | + | magnitude (smallest first): |
| − | + | ||
| − | + | ||
| Line 2,958: | Line 2,975: | ||
|} | |} | ||
| − | + | ||
| − | + | ||
| Line 2,974: | Line 2,991: | ||
| − | [[Image:KOER-%20Mathematics%20-%20Statistics_html_58d59706.png]] | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_58d59706.png]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
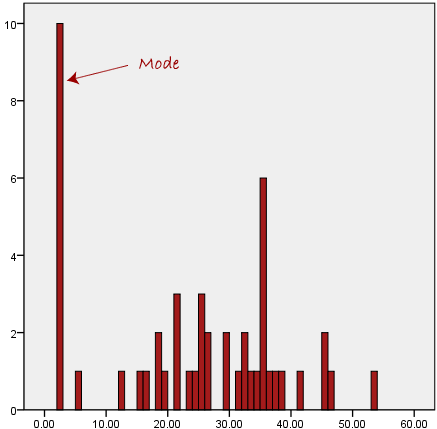
| − | + | Normally, the mode is used for categorical data | |
| − | + | where we wish to know which is the most common category as | |
| + | illustrated below: | ||
| − | + | We can see above that the most common form of | |
| − | + | transport, in this particular data set, is the bus. However, one of | |
| + | the problems with the mode is that it is not unique, so it leaves us | ||
| + | with problems when we have two or more values that share the highest | ||
| + | frequency, such as below: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_m64bbad46.png]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | + | We are now stuck as to which mode best describes | |
| − | + | the central tendency of the data. This is particularly problematic | |
| − | + | when we have continuous data, as we are more likely not to have any | |
| + | one value that is more frequent than the other. For example, consider | ||
| + | measuring 30 peoples' weight (to the nearest 0.1 kg). How likely is | ||
| + | it that we will find two or more people with '''exactly''' | ||
| + | the same weight, e.g. 67.4 kg? The answer, is probably very unlikely | ||
| + | - many people might be close but with such a small sample (30 people) | ||
| + | and a large range of possible weights you are unlikely to find two | ||
| + | people with exactly the same weight, that is, to the nearest 0.1 kg. | ||
| + | This is why the mode is very rarely used with continuous data. | ||
| − | + | ||
| − | + | ||
| − | + | Another problem with the mode is that it will not | |
| − | + | provide us with a very good measure of central tendency when the most | |
| − | + | common mark is far away from the rest of the data in the data set, as | |
| + | depicted in the diagram below: | ||
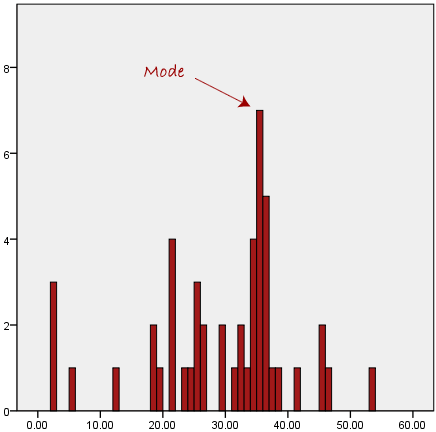
| − | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_152dd141.png]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | |||
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | |||
| + | |||
| − | + | ||
| + | |||
| − | + | ||
| + | |||
| + | |||
| − | + | ||
| + | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In the above diagram the mode has a value of 2. We | |
| − | + | can clearly see, however, that the mode is not representative of the | |
| + | data, which is mostly concentrated around the 20 to 30 value range. | ||
| + | To use the mode to describe the central tendency of this data set | ||
| + | would be misleading. | ||
| − | + | == Skewed Distributions and the Mean and Median == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_26c6186d.png]]We | |
| − | + | often test whether our data is normally distributed as this is a | |
| + | common assumption underlying many statistical tests. An example of a | ||
| + | normally distributed set of data is presented below: | ||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | When you have a normally distributed sample you | |
| − | + | can legitimately use both the mean or the median as your measure of | |
| − | + | central tendency. In fact, in any symmetrical distribution the mean, | |
| + | median and mode are equal. However, in this situation, the mean is | ||
| + | widely preferred as the best measure of central tendency as it is the | ||
| + | measure that includes all the values in the data set for its | ||
| + | calculation, and any change in any of the scores will affect the | ||
| + | value of the mean. This is not the case with the median or mode. | ||
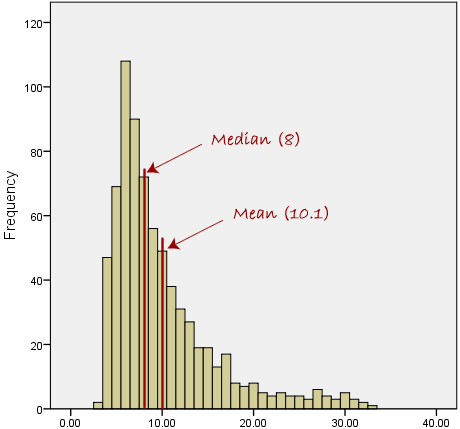
| − | + | However, when our data is skewed, for example, as | |
| + | with the right-skewed data set below: | ||
| + | |||
| − | + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_m2609c500.png]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
| + | |||
| − | + | ||
| + | |||
| + | |||
| − | + | ||
| + | |||
| + | |||
| − | + | ||
| + | |||
| + | |||
| − | + | ||
| + | |||
| + | |||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
| + | |||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | we find that the mean is being dragged in the | |
| + | direct of the skew. In these situations, the median is generally | ||
| + | considered to be the best representative of the central location of | ||
| + | the data. The more skewed the distribution the greater the difference | ||
| + | between the median and mean, and the greater emphasis should be | ||
| + | placed on using the median as opposed to the mean. A classic example | ||
| + | of the above right-skewed distribution is income (salary), where | ||
| + | higher-earners provide a false representation of the typical income | ||
| + | if expressed as a mean and not a median. | ||
| − | + | If dealing with a normal distribution, and tests | |
| − | + | of normality show that the data is non-normal, then it is customary | |
| − | + | to use the median instead of the mean. This is more a rule of thumb | |
| − | + | than a strict guideline however. Sometimes, researchers wish to | |
| + | report the mean of a skewed distribution if the median and mean are | ||
| + | not appreciably different (a subjective assessment) and if it allows | ||
| + | easier comparisons to previous research to be made. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Summary of when to use the mean, median and mode == | |
| − | |||
| − | + | Please use the following summary table to know | |
| + | what the best measure of central tendency is with respect to the | ||
| + | different types of variables. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | {| border="1" | |
| + | |- | ||
| + | | | ||
| + | '''Type of Variable''' | ||
| − | + | | | |
| + | '''Best measure of central tendency''' | ||
| − | + | |- | |
| + | | | ||
| + | Nominal | ||
| − | + | | | |
| + | Mode | ||
| − | + | |- | |
| + | | | ||
| + | Ordinal | ||
| − | + | | | |
| + | Median | ||
| − | + | |- | |
| − | + | | | |
| + | Interval/Ratio (not skewed) | ||
| − | + | | | |
| − | + | Mean | |
| − | + | |- | |
| − | + | | | |
| − | + | Interval/Ratio (skewed) | |
| − | |||
| − | + | | | |
| − | + | Median | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Relative advantages and disadvantages of mean, median and mode == | |
| − | |||
| − | |||
| − | + | Mean. | |
| − | + | Advantages: | |
| − | + | Finds the most accurate average of the set of numbers. | |
| − | the | + | Disadvantages: |
| − | + | Outliers (few values are very different from most) can change the | |
| − | + | mean a lot... making it much lower/higher than it should | |
| − | + | be. | |
| − | + | ||
| + | Median: | ||
| + | Advantages: Finds the middle number of a set of | ||
| + | data, so outliers have little or no effect. | ||
| + | Disadvantages: If the | ||
| + | gap between some numbers is large, while it is small between other | ||
| + | numbers in the data, this can cause the median to be a very | ||
| + | inaccurate way to find the middle of a set of | ||
| + | values. | ||
| + | |||
| + | Mode: | ||
| + | Advantages: Allows you to see what value | ||
| + | happened the most in a set of data. This can help you to figure out | ||
| + | things in a different way. It is also quick and easy. | ||
| + | Disadvantages: | ||
| + | Could be very far from the actual middle of the data. The least | ||
| + | reliable way to find the middle or average of the data. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | This means that each of | |
| − | + | these measures can be useful in different kinds of distributions. | |
| − | |||
| − | |||
| − | |||
| − | = | + | == Activities == |
| − | |||
| − | + | == Activity 1 : Central Tendency == | |
| − | |||
| − | |||
| − | + | ==== Learning Objectives ==== | |
| − | |||
| − | |||
| − | |||
| − | + | Learn to calculate each average measure - Mean, | |
| − | + | Median, Mode. And understand the difference between them. Know in | |
| + | which situation which measure must be used. | ||
| − | + | ==== Pre-requisites/ Instructions ==== | |
| − | + | ||
| − | + | ||
| + | |||
| − | == | + | ==== Materials and Resources Required ==== |
| − | + | Paper and Pencil | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ==== Method ==== |
| − | + | Solve the problems A and B | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | and | ||
| − | |||
| − | + | ||
| + | |||
| + | |||
| − | + | A. 27 members of a | |
| − | + | class were given a puzzle to solve and the times (in minutes) each | |
| − | + | pupil took to solve it were noted. | |
| − | |||
| − | |||
| − | |||
| − | = | + | |
| + | |||
| + | |||
| + | |||
| + | {| border="1" | ||
| + | |- | ||
| + | | | ||
| + | '''the times (in minutes) each pupil took''' | ||
| + | |||
| − | + | |- | |
| − | + | | | |
| − | + | 19 14 15 9 18 16 10 11 16 | |
| − | + | 4 20 10 14 11 9 13 15 13 | |
| − | |||
| − | |||
| − | + | 12 2 17 15 14 10 11 10 12 | |
| − | |||
| − | |||
| − | |||
| − | + | |} | |
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # The MEAN value of a set of data is Sum of Values / Number of Values . What is the mean (to 2 decimal places) of the times given in the table? | |
| + | # The MEDIAN is the middle value of an ordered set of data. | ||
| + | ## Write down the times in the table above in ascending order. | ||
| + | ## How many values are there? | ||
| + | ## What is the median ? | ||
| + | # | ||
| + | # The MODE is the value which occurs most often, i.e. the most popular. | ||
| + | ## What is the mode of the times in the table above? | ||
| + | # | ||
| + | # Which of the three measures do you think is most representative of the average time? In this case it is probably the mean, but this will not always be so. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''B Choosing which measure to use ''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The | + | The sales in one week of a particular dress are |
| − | + | given in terms of the dress sizes. | |
| − | + | # Determine the mean, median and mode for this data . | |
| + | # What is the size that is sold the most ? | ||
| + | # Which of these measures is of most use? | ||
| + | |||
| + | |||
| + | |||
| − | + | Dress sizes sold in one week | |
| + | |||
| + | |||
| + | {| border="1" | ||
| + | |- | ||
| + | | | ||
| + | 10 | ||
| − | + | 16 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 16 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 12 | |
| − | |||
| − | + | 16 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | | | |
| − | + | 14 | |
| − | + | 12 | |
| + | |||
| + | |||
| + | 14 | ||
| + | |||
| − | + | 16 | |
| − | |||
| − | + | 18 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | | | |
| − | + | 12 | |
| − | + | 10 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 18 | |
| − | |||
| − | + | 10 | |
| + | |||
| − | + | 14 | |
| − | |||
| − | + | | | |
| − | + | 16 | |
| − | + | ||
| − | + | ||
| − | + | 14 | |
| − | + | ||
| − | + | ||
| − | + | 8 | |
| − | + | ||
| − | + | ||
| − | + | 10 | |
| − | + | 16 | |
| − | |||
| − | + | | | |
| − | + | 18 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 16 | |
| − | === Coefficient of variation === | + | 14 |
| + | |||
| + | |||
| + | 16 | ||
| + | |||
| + | |||
| + | 8 | ||
| + | |||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==== Evaluation ==== | ||
| + | |||
| + | # Does the student understand the difference between Mean, Median and Mode | ||
| + | # Can the student calculate each of the measures ? | ||
| + | # Does the student know which measure is useful and represents the actual data given a data set ? | ||
| + | |||
| + | == Self-Evaluation == | ||
| + | |||
| + | == Further Explorations == | ||
| + | |||
| + | == Enrichment Activities == | ||
| + | |||
| + | = Dispersion = | ||
| + | |||
| + | == Introduction == | ||
| + | |||
| + | A measure of spread, sometimes also called a | ||
| + | measure of dispersion, is used to describe the variability in a | ||
| + | sample or population. It is usually used in conjunction with a | ||
| + | measure of central tendency, such as, the mean or median, to provide | ||
| + | an overall description of a set of data. | ||
| + | |||
| + | |||
| + | There are many reasons why the measure of the | ||
| + | spread of data values is important but one of the main reasons | ||
| + | regards its relationship with measures of central tendency. A measure | ||
| + | of spread gives us an idea of how well the mean, for example, | ||
| + | represents the data. If the spread of values in the data set is large | ||
| + | then the mean is not as representative of the data as if the spread | ||
| + | of data is small. This is because a large spread indicates that there | ||
| + | are probably large differences between individual scores. | ||
| + | Additionally, in research, it is often seen as positive if there is | ||
| + | little variation in each data group as it indicates that the similar. | ||
| + | |||
| + | |||
| + | We will be looking at the range, quartiles, | ||
| + | variance, absolute deviation and standard deviation. | ||
| + | |||
| + | |||
| + | == Objectives == | ||
| + | |||
| + | * Understand that a measure of dispersion is a measure of spread, is used to describe the variability in a sample or population. | ||
| + | * It is usually used in conjunction with a measure of central tendency, such as, the mean or median, to provide an overall description of a set of data. | ||
| + | * It important to measure the spread of data because we can understand its relationship with measures of central tendency to make more accurate interpretation of data. | ||
| + | * Understand and know the terms:Range, Quartile, Standard Deviation , Cumulative Frequency | ||
| + | * Calculation of Co-efficient of Variation. Meaning and interpretation of C.V. Analyse data and make conclusions | ||
| + | |||
| + | == Range == | ||
| + | |||
| + | The range is the difference between the highest | ||
| + | and lowest scores in a data set and is the simplest measure of | ||
| + | spread. So we calculate range as: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Range = maximum value - minimum value | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | For example, let us consider the following data | ||
| + | set: | ||
| + | |||
| + | |||
| + | 23 56 45 65 59 55 62 54 85 25 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | The maximum value is 85 and the minimum value is | ||
| + | 23. This results in a range of 62, which is 85 minus 23. Whilst using | ||
| + | the range as a measure of spread is limited, it does set the | ||
| + | boundaries of the scores. This can be useful if you are measuring a | ||
| + | variable that has either a critical low or high threshold (or both) | ||
| + | that should not be crossed. The range will instantly inform you | ||
| + | whether at least one value broke these critical thresholds. In | ||
| + | addition, the range can be used to detect any errors when entering | ||
| + | data. For example, if you have recorded the age of school children in | ||
| + | your study and your range is 7 to 123 years old you know you have | ||
| + | made a mistake! | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | === Quartiles and Interquartile Range === | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Quartiles tell us about the spread of a data set | ||
| + | by breaking the data set into quarters, just like the median breaks | ||
| + | it in half. For example, consider the marks of the 100 students | ||
| + | below, which have been ordered from the lowest to the highest scores, | ||
| + | and the quartiles highlighted in red. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Order Score Order Score Order Score Order | ||
| + | Score Order Score | ||
| + | |||
| + | |||
| + | 1st 35 21st 42 41st 53 61st 64 81st 74 | ||
| + | |||
| + | |||
| + | 2nd 37 22nd 42 42nd 53 62nd 64 82nd 74 | ||
| + | |||
| + | |||
| + | 3rd 37 23rd 44 43rd 54 63rd 65 83rd 74 | ||
| + | |||
| + | |||
| + | 4th 38 24th 44 44th 55 64th 66 84th 75 | ||
| + | |||
| + | |||
| + | 5th 39 25th 45 45th 55 65th 67 85th 75 | ||
| + | |||
| + | |||
| + | 6th 39 26th 45 46th 56 66th 67 86th 76 | ||
| + | |||
| + | |||
| + | 7th 39 27th 45 47th 57 67th 67 87th 77 | ||
| + | |||
| + | |||
| + | 8th 39 28th 45 48th 57 68th 67 88th 77 | ||
| + | |||
| + | |||
| + | 9th 39 29th 47 49th 58 69th 68 89th 79 | ||
| + | |||
| + | |||
| + | 10th 40 30th 48 50th 58 70th 69 90th 80 | ||
| + | |||
| + | |||
| + | 11th 40 31st 49 51st 59 71st 69 91st 81 | ||
| + | |||
| + | |||
| + | 12th 40 32nd 49 52nd 60 72nd 69 92nd 81 | ||
| + | |||
| + | |||
| + | 13th 40 33rd 49 53rd 61 73rd 70 93rd 81 | ||
| + | |||
| + | |||
| + | 14th 40 34th 49 54th 62 74th 70 94th 81 | ||
| + | |||
| + | |||
| + | 15th 40 35th 51 55th 62 75th 71 95th 81 | ||
| + | |||
| + | |||
| + | 16th 41 36th 51 56th 62 76th 71 96th 81 | ||
| + | |||
| + | |||
| + | 17th 41 37th 51 57th 63 77th 71 97th 83 | ||
| + | |||
| + | |||
| + | 18th 42 38th 51 58th 63 78th 72 98th 84 | ||
| + | |||
| + | |||
| + | 19th 42 39th 52 59th 64 79th 74 99th 84 | ||
| + | |||
| + | |||
| + | 20th 42 40th 52 60th 64 80th 74 100th 85 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | The first quartile (Q1) lies between the 25th and | ||
| + | 26th student's marks, the second quartile (Q2) between the 50th and | ||
| + | 51st student's marks, and the third quartile (Q3) between the 75th | ||
| + | and 76th student's marks. Hence: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | First quartile (Q1) = 45 + 45 ÷ 2 = 45 | ||
| + | |||
| + | |||
| + | Second quartile (Q2) = 58 + 59 ÷ 2 = 58.5 | ||
| + | |||
| + | |||
| + | Third quartile (Q3) = 71 + 71 ÷ 2 = 71 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | In the above example, we have an even number of | ||
| + | scores (100 students rather than an odd number such as 99 students). | ||
| + | This means that when we calculate the quartiles, we take the sum of | ||
| + | the two scores around each quartile and then half them (hence Q1= 45 | ||
| + | + 45 ÷ 2 = 45) . However, if we had an odd number of scores (say, 99 | ||
| + | students), then we would only need to take one score for each | ||
| + | quartile (that is, the 25th, 50th and 75th scores). You should | ||
| + | recognize that the second quartile is also the median. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Quartiles are a useful measure of spread because | ||
| + | they are much less affected by outliers or a skewed data set than the | ||
| + | equivalent measures of mean and standard deviation. For this reason, | ||
| + | quartiles are often reported along with the median as the best choice | ||
| + | of measure of spread and central tendency, respectively, when dealing | ||
| + | with skewed and/or data with outliers. A common way of expressing | ||
| + | quartiles is as an interquartile range. The interquartile range | ||
| + | describes the difference between the third quartile (Q3) and the | ||
| + | first quartile (Q1), telling us about the range of the middle half of | ||
| + | the scores in the distribution. Hence, for our 100 students: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Interquartile range = Q3 - Q1 | ||
| + | |||
| + | |||
| + | = 71 - 45 | ||
| + | |||
| + | |||
| + | = 26 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | However, it should be noted that in journals and | ||
| + | other publications you will usually see the interquartile range | ||
| + | reported as 45 to 71, rather than the calculated range. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | A slight variation on this is the | ||
| + | semi-interquartile range, which is half the interquartile range = ½ | ||
| + | (Q3 - Q1). Hence, for our 100 students, this would be 26 ÷ 2 = 13. | ||
| + | |||
| + | |||
| + | == Standard Deviation == | ||
| + | |||
| + | The standard deviation is a measure of the spread | ||
| + | of scores within a set of data. Usually, we are interested in the | ||
| + | standard deviation of a population. However, as we are often | ||
| + | presented with data from a sample only, we can estimate the | ||
| + | population standard deviation from a sample standard deviation. These | ||
| + | two standard deviations, sample and population standard deviations, | ||
| + | are calculated differently. In statistics we are usually presented | ||
| + | with having to calculate sample standard deviations, and so this is | ||
| + | what this article will focus on, although the formula for a | ||
| + | population standard deviation will also be shown. | ||
| + | |||
| + | |||
| + | === When to use the sample or population standard deviation === | ||
| + | |||
| + | We are normally interested in knowing the | ||
| + | population standard deviation as our population contains all the | ||
| + | values we are interested in. Therefore, you would normally calculate | ||
| + | the population standard deviation if: (1) you have the entire | ||
| + | population or (2) you have a sample of a larger population but you | ||
| + | are only interested in this sample and do not wish to generalize your | ||
| + | findings to the population. However, in statistics, we are usually | ||
| + | presented with a sample from which we wish to estimate (generalize | ||
| + | to) a population, and the standard deviation is no exception to this. | ||
| + | Therefore, if all you have is a sample but you wish to make a | ||
| + | statement about the population standard deviation from which the | ||
| + | sample is drawn, then you need to use the sample standard deviation. | ||
| + | Confusion can often arise as to which standard deviation to use due | ||
| + | to the name "sample" standard deviation incorrectly being | ||
| + | interpreted as meaning the standard deviation of the sample itself | ||
| + | and not as the estimate of the population standard deviation based on | ||
| + | the sample. | ||
| + | |||
| + | |||
| + | === What type of data should you use when you calculate a standard deviation? === | ||
| + | |||
| + | The standard deviation is used in conjunction with | ||
| + | the mean, to summarise [[continuous]] | ||
| + | data not categorical data. In addition, the standard deviation, like | ||
| + | the [[mean]], | ||
| + | is normally only appropriate when the continuous data is not | ||
| + | significantly skewed or has outliers. | ||
| + | |||
| + | |||
| + | === Examples of when to use the sample or population standard deviation === | ||
| + | |||
| + | Q. A teacher sets an exam for their pupils. The | ||
| + | teacher wants to summarize the results the pupils attained as a mean | ||
| + | and standard deviation. Which standard deviation should be used? | ||
| + | |||
| + | |||
| + | A. Population standard deviation. Why? Because the | ||
| + | teacher is only interested in this class of pupils' scores and nobody | ||
| + | else. | ||
| + | |||
| + | |||
| + | Q. A researcher has recruited males aged 45 to 65 | ||
| + | years old for an exercise training study to investigate risk markers | ||
| + | for heart disease, e.g. cholesterol. Which standard deviation would | ||
| + | most likely be used? | ||
| + | |||
| + | |||
| + | A. Sample standard deviation. Although not | ||
| + | explicitly stated, a researcher investigating health related issues | ||
| + | will not be simply concerned with just the participants of their | ||
| + | study; they will want to show how their sample results can be | ||
| + | generalised to the whole population (in this case, males aged 45 to | ||
| + | 65 years old). Hence, the use of the sample standard deviation. | ||
| + | |||
| + | |||
| + | Q. One of the questions on a national consensus | ||
| + | survey asks for respondent's age. Which standard deviation would be | ||
| + | used to describe the variation in all ages received from the | ||
| + | consensus? | ||
| + | |||
| + | |||
| + | A. Population standard deviation. A national | ||
| + | consensus is used to find out information about the nation's | ||
| + | citizens. By definition, it includes the whole population, therefore, | ||
| + | a population standard deviation would be used. | ||
| + | |||
| + | |||
| + | === What are the formulas for the standard deviation? === | ||
| + | |||
| + | The '''sample standard deviation formula''' | ||
| + | is: | ||
| + | |||
| + | |||
| + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_m5610ded5.gif]] | ||
| + | |||
| + | |||
| + | where, | ||
| + | |||
| + | |||
| + | s = sample standard | ||
| + | deviation | ||
| + | Σ = sum | ||
| + | of... | ||
| + | X = sample mean | ||
| + | n = number of scores in sample. | ||
| + | |||
| + | |||
| + | The '''population standard deviation''' | ||
| + | formula is: | ||
| + | |||
| + | |||
| + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_m48922b88.gif]] | ||
| + | |||
| + | |||
| + | where, | ||
| + | |||
| + | |||
| + | σ | ||
| + | = population standard deviation | ||
| + | Σ | ||
| + | = sum of... | ||
| + | μ = | ||
| + | population mean | ||
| + | n = number of scores in sample. | ||
| + | |||
| + | |||
| + | == Variation == | ||
| + | |||
| + | Quartiles are useful but they are also somewhat | ||
| + | limited because they do not take into account every score in our | ||
| + | group of data. To get a more representative idea of spread we need to | ||
| + | take into account the actual values of each score in a data set. The | ||
| + | absolute deviation, variance and standard deviation are such | ||
| + | measures. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | The absolute and mean absolute deviation show the | ||
| + | amount of deviation (variation) that occurs around the mean score. To | ||
| + | find the total variability in our group of data, we simply add up the | ||
| + | deviation of each score from the mean. The average deviation of a | ||
| + | score can then be calculated by dividing this total by the number of | ||
| + | scores. How we calculate the deviation of a score from the mean | ||
| + | depends on our choice of statistic, whether we use absolute | ||
| + | deviation, variance or standard deviation. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | === Absolute Deviation and Mean Absolute Deviation === | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Perhaps the simplest way of calculating the | ||
| + | deviation of a score from the mean is to take each score and minus | ||
| + | the mean score. For example, the mean score for the group of 100 | ||
| + | students we used earlier was 58.75 out of 100. Therefore, if we took | ||
| + | a student that scored 60 out of 100, the deviation of a score from | ||
| + | the mean is 60 - 58.75 = 1.25. It is important to note that scores | ||
| + | above the mean have positive deviations (as demonstrated above) | ||
| + | whilst that scores below the mean will have negative deviations. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | To find out the total variability in our data set, | ||
| + | we would perform this calculation for all of the 100 students' | ||
| + | scores. However, the problem is that because we have both positive | ||
| + | and minus signs, when we add up all of these deviations, they cancel | ||
| + | each other out, giving us a total deviation of zero. Since we are | ||
| + | only interested in the deviations of the scores and not whether they | ||
| + | are above or below the mean score, we can ignore the minus sign and | ||
| + | take only the absolute value, giving us the absolute deviation. | ||
| + | Adding up all of these absolute deviations and dividing them by the | ||
| + | total number of scores then gives us the mean absolute deviation (see | ||
| + | below). Therefore, for our 100 students the mean absolute deviation | ||
| + | is 12.81, as shown below: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | === Variance === | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Another method for calculating the deviation of a | ||
| + | group of scores from the mean, such as the 100 students we used | ||
| + | earlier, is to use the variance. Unlike the absolute deviation, which | ||
| + | uses the absolute value of the deviation in order to "rid | ||
| + | itself" of the negative values, the variance achieves positive | ||
| + | values by squaring each of the deviations instead. Adding up these | ||
| + | squared deviations gives us the sum of squares, which we can then | ||
| + | divide by the total number of scores in our group of data (in other | ||
| + | words, 100 because there are 100 students) to find the variance (see | ||
| + | below). Therefore, for our 100 students, the variance is 211.89, as | ||
| + | shown below: | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | As a measure of variability, the variance is | ||
| + | useful. If the scores in our group of data are spread out then the | ||
| + | variance will be a large number. Conversely, if the scores are spread | ||
| + | closely around the mean, then the variance will be a smaller number. | ||
| + | However, there are two potential problems with the variance. First, | ||
| + | because the deviations of scores from the mean are 'squared', this | ||
| + | gives more weight to extreme scores. If our data contains outliers | ||
| + | (in other words, one or a small number of scores that are | ||
| + | particularly far away from the mean and perhaps do not represent well | ||
| + | our data as a whole) this can give undo weight to these scores. | ||
| + | Secondly, the variance is not in the same units as the scores in our | ||
| + | data set: variance is measured in the units squared. This means we | ||
| + | cannot place it on our frequency distribution and cannot directly | ||
| + | relate its value to the values in our data set. Therefore, the figure | ||
| + | of 211.89, our variance, appears somewhat arbitrary. Calculating the | ||
| + | standard deviation rather than the variance rectifies this problem. | ||
| + | Nonetheless, analysing variance is extremely important in some | ||
| + | statistical analyses, discussed in other statistical guides. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | === Coefficient of variation === | ||
Coefficient of | Coefficient of | ||
| − | variation is defined as | + | variation is defined as |
| + | |||
| + | |||
| + | [[Image:KOER-%20Mathematics%20-%20Statistics_html_1afc44b3.png]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | where v is the standard | ||
| + | deviation and x is the mean of the given data. It is also called as | ||
| + | |||
| + | |||
| + | a relative standard | ||
| + | deviation. | ||
| + | |||
| + | |||
| + | '''Remarks ''' | ||
| + | |||
| + | |||
| + | * The coefficient of variation helps us to compare the consistency of two or more | ||
| + | * collections of data. | ||
| + | * When the coefficient of variation is more, the given data is less consistent. | ||
| + | * When the coefficient of variation is less, the given data is more consistent. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Self-Evaluation == | ||
| + | |||
| + | == Further Explorations == | ||
| + | |||
| + | == Enrichment Activities == | ||
| + | |||
| + | = See Also = | ||
| + | |||
| + | Statistics | ||
| + | on Wikipedia [[http://en.wikipedia.org/wiki/Statistics]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 4,224: | Line 4,241: | ||
"Figuring and society" by Ronald Meek, | "Figuring and society" by Ronald Meek, | ||
Fontana ISBN 0 00 632560 | Fontana ISBN 0 00 632560 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 09:13, 4 January 2013
Statistics
Introduction
The following is a background literature for teachers. It summarises the things to be known to a teacher to teach this topic more effectively . This literature is meant to be a ready reference for the teacher to develop the concepts, inculcate necessary skills, and impart knowledge in Statistics from Class 6 to Class 10.
The teacher will get an overall idea of all the
sub topics required for school level statistics. The flow of how to
build/develop an understanding of the topic for students from basics
to more advanced aspects. Each subtopic will be developed by way of
introductions, objectives, activities, evaluation and advanced and
additional information and resources.
Statistics
In early times, the meaning of statistics was restricted to information about states ( any political organization with a government that has supreme independent authority over a geographic area). This was later extended to include all collections of information of all types, and later still it was extended to include the analysis and interpretation of such data. In modern terms, "statistics" means both sets of collected information and analytical work which requires statistical inference.
Doing statistical analysis it is possible to test
numerical data for relevance, reliability and validity. In order to
do this, statisticians must present data in such a form that others
can utilise the relevant information to enable them to make
judgements. One view is that the study of statistics is reported to
have started with the Englishman, John Graunt (1620 – 1674), who
collected and studied the death records in various cities of Britain.
He was fascinated by the patterns he found in the whole population.
Much of current day statistical analysis is of quite recent
development, the availability of cheap computing power acting as a
catalyst for the development of appropriate ways of presenting and
analysing data. In fact, the more advanced statistical analyses and
tests are based on probability theory, developed over the past few
centuries, but put into a more modern context by mathematical
statisticians such as Karl Pearson (1857 – 1936) , Sir Ronald
Fisher (1890 – 1962) , Jerzy Neyman (1894 – 1981).
The curricular objectives for school level
statistical work can be described as follows:
- To understand the meaning of data. The need for statistics and how to collect, organise and represent data in different ways.
- Skills to represent and analyse data in tabular and graphical forms.
- Understanding central tendency and computation of the measure of central tendency namely arithmetic mean, median and mode for both grouped and non-grouped data. Have the ability to use the appropriate central tendency to represent the data appropriately.
- Understanding dispersion determine the measures of dispersion such as range quartile deviation, mean deviation and standard deviation.
- Understand the limitations and drawbacks of statistics
Descriptive and Inferential Statistics
When analysing data, for example, the marks achieved by 100 students for a piece of coursework, it is possible to use both descriptive and inferential statistics in your analysis of their marks. Typically, in most research conducted on groups of people, you will use both descriptive and inferential statistics to analyse your results and draw conclusions. So what are descriptive and inferential statistics? And what are their differences?
Descriptive Statistics
Descriptive statistics is the term given to the analysis of data that helps describe, show or summarize data in a meaningful way such that, for example, patterns might emerge from the data. Descriptive statistics do not, however, allow us to make conclusions beyond the data we have analysed or reach conclusions regarding any hypotheses we might have made. They are simply a way to describe our data.
Descriptive statistics are very important, as if
we simply presented our raw data it would be hard to visualize what
the data was showing, especially if there was a lot of it.
Descriptive statistics therefore allow us to present the data in a
more meaningful way which allows simpler interpretation of the data.
For example, if we had the results of 100 pieces of students'
coursework, we may be interested in the overall performance of those
students. We would also be interested in the distribution or spread
of the marks. Descriptive statistics allow us to do this. How to
properly describe data through statistics and graphs is an important
topic and discussed in other Laerd Statistics Guides. Typically,
there are two general types of statistic that are used to describe
data:
Measures of central tendency: these are
ways of describing the central position of a frequency distribution
for a group of data. In this case, the frequency distribution is
simply the distribution and pattern of marks scored by the 100
students from the lowest to the highest. We can describe this central
position using a number of statistics, including the mode, median,
and mean. You can read about measures of central tendency here.
Measures of spread: these are ways of
summarizing a group of data by describing how spread out the scores
are. For example, the mean score of our 100 students may be 65 out of
100. However, not all students will have scored 65 marks. Rather,
their scores will be spread out. Some will be lower and others
higher. Measures of spread help us to summarize how spread out these
scores are. To describe this spread, a number of statistics are
available to us, including the range, quartiles, absolute deviation,
variance and standard deviation.
When we use descriptive statistics it is useful to
summarize our group of data using a combination of tabulated
description (i.e. tables), graphical description (i.e. graphs and
charts) and statistical commentary (i.e. a discussion of the
results).
Inferential Statistics
We have seen that descriptive statistics provide information about our immediate group of data. For example, we could calculate the mean and standard deviation of the exam marks for the 100 students and this could provide valuable information about this group of 100 students. Any group of data like this, that includes all the data you are interested, in is called a population. A population can be small or large, as long as it includes all the data you are interested in. For example, if you were only interested in the exam marks of 100 students, then the 100 students would represent your population. Descriptive statistics are applied to populations and the properties of populations, like the mean or standard deviation, are called parameters as they represent the whole population (i.e. everybody you are interested in).
Often, however, you do not have access to the
whole population you are interested in investigating but only have a
limited number of data instead. For example, you might be interested
in the exam marks of all students in the UK. It is not feasible to
measure all exam marks of all students in the whole of the UK so you
have to measure a smaller sample of students, for example, 100
students, that are used to represent the larger population of all UK
students. Properties of samples, such as the mean or standard
deviation, are not called parameters but statistics. Inferential
statistics are techniques that allow us to use these samples to make
generalizations about the populations from which the samples were
drawn. It is, therefore, important the sample accurately represents
the population. The process of achieving this is called sampling.
Inferential statistics arise out of the fact that sampling naturally
incurs sampling error and thus a sample is not expected to perfectly
represent the population. The methods of inferential statistics are
(1) the estimation of parameter(s) and (2) testing of statistical
hypotheses.
Mind Map
Data Handling
Introduction
Data is a collection of facts, such as values or measurements. It can be numbers, words, measurements, observations or even just descriptions of things. Statistical work is done for problem solving. For problem solving, we first have to understand the problem (postulating hypotheses ) , then we have to collect relevant data , after which we must be able to present the data, finally analyse the data and make conclusions related to the original hypotheses. Statistics provides us with tools to analyse data and draw conclusions from a large set of data by organising the data in the set in different ways and analysing the data by observing patterns. Data handling would include identifying data, collecting data, organising/representing data and summarising data.
Objective
- What is statistical work and why and where we would need to use this.
- To understand different types of data: qualitative and quantitative
- To understand the sources of data : Primary and Secondary
- To learn how to collect, classify and display data; data is information that is used in any process connected with statistics.
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables.Data refers to the pieces of information that have been observed and recorded, from an experiment or a survey. There are two types of data: primary and secondary. The word ”data” is the plural of the word ”datum”, and therefore one should say, ”the data are” and not ”the data is”. Data can be classified as primary or secondary, and primary or secondary data can be classified as qualitative or quantitative.
The figure below summarises the classifications of
data. Primary data describes the original data that have been
collected. This type of data is also known as raw data. Often the
primary data set is very large and is therefore summarised or
processed to extract meaningful information. Qualitative data is
information that cannot be written as numbers, for example, if you
were collecting data from people on how they feel or what their
favourite colour is.Quantitative data is information that can be
written as numbers, for example, if you were collecting data from
people on their height or weight.
Secondary data is
primary data that has been summarised or processed, for example, the
set
of colours that people
gave as favourite colours would be secondary data because it is a
summary of responses.
Data already collected prior our use is secondary data. Primary data
is what we collect as a part of our study. All processed data
therefore is also secondary.
Transforming primary data into secondary data through analysis, grouping or organisation into secondary data is the process of generating information.
Purpose of Collecting Primary Data
Data is collected to provide answers that help with understanding a particular situation. Here are examples to illustrate some real world data collections scenarios in the categories of qualitative and quantitative data.
Qualitative Data
- The local government might want to know how many residents have electricity and might ask the question: ”Does your home have a safe supply of electricity?”
- A supermarket manager might ask the question: “What flavours of soft drink should be stocked in my supermarket?” The question asked of customers might be “What is your favourite soft drink?” Based on the customers’ responses, the manager can make an informed decision as to what soft drinks to stock.
- A company manufacturing medicines might ask “How effective is our pill at relieving a headache?” The question asked of people using the pill for a headache might be: “Does taking the pill relieve your headache?” Based on responses, the company learns how effective their product is.
- A motor car company might want to improve their customer service, and might ask their customers: “How can we improve our customer service?”
- A teacher may ask “How many hours of TV by students on TV' to get an idea of what children are learning from TV at home and how it supplements (or affects) the learning in the school
Quantitative Data
- A cell phone manufacturing company might collect data about how often people buy new cell phones and what factors affect their choice, so that the cell phone company can focus on those features that would make their product more attractive to buyers.
- A town councillor might want to know how many accidents have occurred at a particular intersection, to decide whether a robot should be installed. The councillor would visit the local police station to research their records to collect the appropriate data.
- A supermarket manager might ask the question: “What flavours of soft drink should be stocked in my supermarket?” The question asked of customers might be “What is your favourite soft drink?” Based on the customers’ responses, the manager can make an informed decision as to what soft drinks to stock.
- What kind of TV programs are watched by students, how many are educational in nature.
However, it is important to note that different questions reveal different features of a situation, and that this affects the ability to understand the situation. For example, if the question in the list What kind of TV programs are watched by students, how many are educational in nature. was re-phrased to be: Do your children watch educational programs on TV and if you answered yes, but most programs being watched were of entertainment value, , then this could give the wrong impression that TV was being used as an educational tool in your home .
Data Collection
The method of collecting the data must be appropriate to the question being asked. Some
examples of data
collecting methods are:
- Experiments
- Questionnaires, surveys, focus group discussions and interviews
- Other sources (friends, family, newspapers, books, magazines and now increasingly the Internet)
- Observation
- Specialised equipment (rainwater gauges to measure rainfall in a place, various medical equipment that collect information about different biological processes)
The most important
aspect of each method of data collecting is to clearly formulate the
question that is to be answered. The details of the data collection
should therefore be structured to take your question into account.
You must have observed your teacher recording the attendance of students in your class everyday, or recording marks obtained by you after every test or examination. Similarly, you must have also seen a cricket score board. One score boards have been illustrated here :
NatWest One Day International Series: England v India Friday, 16 September 2011 at The Swalec Stadium
England beat India
by 6 wickets (D/L). England won the toss and decided to field
|
|
|
|
India 1st Innings - Close
|
Name
|
Wicket
|
Runs
|
Balls
|
4s
|
6s
| |
|
P Patel
|
c Bresnan
|
b Swann
|
19
|
39
|
0
|
0
|
|
Rahane
|
c Finn
|
b Dernbach
|
26
|
47
|
3
|
0
|
|
Dravid
|
|
b Swann
|
69
|
79
|
4
|
0
|
|
Kohli
|
hit wicket
|
b Swann
|
107
|
93
|
9
|
1
|
|
Raina
|
c Bresnan
|
b Finn
|
15
|
15
|
0
|
1
|
|
Dhoni
|
not out
|
-
|
50
|
26
|
5
|
2
|
|
Jadeja
|
c Bopara
|
b Dernbach
|
0
|
1
|
0
|
0
|
|
Ashwin
|
not out
|
-
|
0
|
0
|
0
|
0
|
|
Extras
|
-
|
6w 1b 11lb
|
18
|
-
| ||
|
Total
|
-
|
for 6
|
304
|
(50.0 ovs)
|
|
Recording Data
Let us take an example of a class which is preparing to go for a picnic. The teacher asked the students to give their choice of fruits out of banana, apple, orange or guava. Uma is asked to prepare the list. She prepared a list of all the children and wrote the choice of fruit against each name. This list would help the teacher to distribute fruits according to the choice.
|
Raghav — Banana
|
Bhawana — Apple
|
Example 1 : A teacher
wants to know the choice of food of each student as part of the
mid-day meal programme. The teacher assigns the task of collecting
this information to Maria. Maria does so using a paper and a pencil.
After arranging the choices in a column, she puts against a choice of
food one ( / ) mark for every student making that choice.
|
Choice
|
Number of students
|
|
Rice only
|
/////////////// //
|
Umesh, after seeing the
table suggested a better method to count the students. He asked
Maria to organise the marks ( / ) in a group of ten as shown below :
|
Choice
|
Tally marks
|
Number of students
|
|
Rice only
|
////////// ///////
|
17
|
Rajan made it simpler by asking her to make groups of five instead of ten, as
shown below :
|
Choice
|
Tally marks
|
Number of students
|
|
Rice only
|
///// ///// ///// //
|
17
|
Meaning of Frequency
Frequency means the number of occurrences within a given time period. It is not easy to answer the question looking at the choices written haphazardly. We arrange the data in Table below using tally marks.
|
Subject
|
Tally Marks
|
Number of Students
|
|
Art
|
///// //
|
7
|
|
Mathematics
|
/////
|
5
|
|
Science
|
///// /
|
6
|
|
English
|
////
|
4
|
The number of tallies before each subject gives the number of students who like that particular subject. This is known as the frequency of that subject. Frequency gives the number of times that a particular entry occurs. From above table, Frequency of students who like English is 4 Frequency of students who like Mathematics is 5 The table made is known as frequency distribution table as it gives the number of times an entry occurs.
Categorical Frequency Distributions
Categorical frequency distributions - can be used for data that can be placed in specific categories, such as nominal- or ordinal-level data. (nominal or ordinal also called discrete data is where we can distinctly count the occurrences of a variable).
Examples - political affiliation, religious affiliation, blood type etc. Below is Blood Type frequency distribution example.
|
Class
|
Frequency
|
Percent
|
|
A
|
5
|
20
|
|
B
|
7
|
28
|
|
C
|
9
|
36
|
|
D
|
4
|
16
|
Activities
Activity 1 Data Collection
Learning Objectives
Understand collection of data .
Materials and resources required
Paper & Pen
Pre-requisites/ Instructions
The meaning of data and how to data is organised in a tabular form
Method
The table below has spaces for up to 10 entries. The first four columns have headings. Choose headings for the other columns and collect data from the 10 of your class mates
|
Name
|
Age
|
Height
|
Favourite Colour
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
Evaluation
Looking at the table and data can the student answer the following questions ?
- Does any student like green the most ?
- Do you think red is the most popular colour, why ?
- What other information did you come to know about each student ?
Evaluation
At the end of this sub-topic the student should be able to
- Identify the different types of data
- Collect, classify and organise data in a tabular form
- Calculate the frequency of data
- Interpret data that is given in a tabular form
Self-Evaluation
Further Explorations
Enrichment Activities
Graphical representation of Data
Introduction
Tabular data can be also represented in the form of a picture ( charts) as visual representations can sometimes be easier to interpret. There are different types of pictorial representations that can be used to represent different type of data.
Objectives
- Understand and know the different pictorial representations: Histogram, Bar Char, Pie Chart
- To be able to look at the data and select the chart that would clearly represent the data as well as convey intended information about the data.
- Understand and know the terms : Frequency Distribution, Class intervals
- To be able to look at a graphical representation and interpret the data
Histogram & Bar Chart
What is a histogram?
A histogram is a plot that lets you discover, and show, the underlying frequency distribution (shape) of a set of continuous data. This allows the inspection of the data for its underlying distribution (e.g. normal distribution), outliers, skewness, etc. An example of a histogram, and the raw data it was constructed from, is shown below:
36 25 38 46 55 68 72 55 36 38
67 45 22 48 91 46
52 61 58 55
How do you construct a histogram from a continuous variable?
To construct a histogram from a continuous variable you first need to split the data into intervals, called bins. In the example above, age has been split into bins, with each bin representing a 10-year period starting at 20 years. Each bin contains the number of occurrences of scores in the data set that are contained within that bin. For the above data set, the frequencies in each bin have been tabulated along with the scores that contributed to the frequency in each bin (see below):
Bin Frequency Scores Included in Bin
20-30 2 25,22
30-40 4 36,38,36,38
40-50 4 46,45,48,46
50-60 5 55,55,52,58,55
60-70 3 68,67,61
70-80 1 72
80-90 0 -
90-100 1 91
Notice that, unlike a bar chart, there are no "gaps" between the bars (although some bars might be "absent" reflecting no frequencies). This is because a histogram represents a continuous data set, and as such, there are no gaps in the data. (Although you will have to decide whether you round up or round down scores on the boundaries of bins)
Choosing the correct bin width
There is no right or wrong answer as to how wide a bin should be, but there are rules of thumb. You need to make sure that the bins are not too small or too large. Consider the histogram we produced earlier (see above): the following histograms use the same data but have either much smaller or larger bins, as shown below:
We can see from the
histogram on the left, that the bin width is too small as it shows
too much individual data and does not allow the underlying pattern
(frequency distribution) of the data to be easily seen. At the other
end of the scale, is the diagram on the right, where the bins are too
large and, again, we are unable to find the underlying trend in the
data.
Histograms are based on
area not height of bars
In a histogram, it is the area of the bar that indicates the frequency of occurrences for each bin. This means that the height of the bar does not necessarily indicate how many occurrences of scores there were within each individual bin. It is the product of height multiplied by the width of the bin that indicates the frequency of occurrences within that bin. One of the reasons that the height of the bars is often incorrectly assessed as indicating frequency and not the area of the bar is due to the fact that a lot of histograms often have equally spaced bars (bins) and, under these circumstances, the height of the bin does reflect the frequency.
What is the difference between a bar chart and a histogram?
The major difference is
that a histogram is only used to plot the frequency of score
occurrences in a continuous data set that has been divided into
classes, called bins. Bar charts, on the other hand, can be used for
a great deal of other types of variables including ordinal and
nominal data sets.
Circle or Pie Chart
 These
are called circle graphs. A circle graph shows the relationship
between a whole and its parts. Here, the whole circle is divided into
sectors. The size of each sector is proportional to the activity or
information it represents.
These
are called circle graphs. A circle graph shows the relationship
between a whole and its parts. Here, the whole circle is divided into
sectors. The size of each sector is proportional to the activity or
information it represents.
A variety of graphical representations of data are now possible using spreadsheet software. OpenOffice CALC can convert a table of data into bar charts, pie charts, area charts etc and make data much more easy to read/interpret.
Activities
Avtivity 2: Histogram and Bar Chart
Learning Objectives
Learn to draw a histogram and bar chart. Understand the difference between a bar chart and a histogram and be able to select the appropriate chart by looking at the problem and data.
Materials and Resources Required
Paper and Pencil
Pre-requisites/ Instructions
Method
Solve the problems A and B
A> In the past year, you have recorded the
number of tickets that a movie theater has sold during each month.
To represent this data set graphically, would you construct a bar
graph or a histogram? Why is this choice better than the other?
Using the following data, construct the graph that you choose.
|
Month
|
Number of Tickets Sold
|
|
January
|
25
|
|
February
|
20
|
|
March
|
15
|
|
April
|
20
|
|
May
|
30
|
|
June
|
35
|
|
July
|
40
|
|
August
|
20
|
|
September
|
25
|
|
October
|
15
|
|
November
|
20
|
|
December
|
30
|
B> For a recent
science project, you collected data regarding the distribution of
fish and aquatic life in a nearby pond. Your data consists of the
number of living creatures found in each 1 meter depth increment in
the pond. Construct a bar graph and several histograms (vary the
depth increment size) for the following data. In which case(s) is the
histogram the same as the bar graph? How do the other histograms vary
from the bar graph?
|
Depth Range
|
Number of Living Creatures
|
|
0 – 1 meters
|
10
|
|
1 – 2 meters
|
93
|
|
2 – 3 meters
|
23
|
|
3 – 4 meters
|
47
|
|
4 – 5 meters
|
68
|
|
5 – 6 meters
|
51
|
|
6 – 7 meters
|
43
|
|
7 – 8 meters
|
21
|
|
8 – 9 meters
|
15
|
|
9 – 10 meters
|
8
|
Evaluation
- Does the student understand the difference between a bar chart and a histogram ?
- Does the student know when to use each of these charts - - depending on the type of data continuous and discrete ?
Evaluation
Self-Evaluation
Further Explorations
Types of Variables
All experiments examine some kind of variable(s). A variable is not only something that we measure, but also something that we can manipulate and something we can control for. To understand the characteristics of variables and how we use them in research, this guide is divided into three main sections. First, we illustrate the role of dependent and independent variables. Second, we discuss the difference between experimental and non-experimental research. Finally, we explain how variables can be characterised as either categorical or continuous.
Dependent and Independent Variables
An independent variable, sometimes called an experimental or predictor variable, is a variable that is being manipulated in an experiment in order to observe the effect on a dependent variable, sometimes called an outcome variable.
Imagine that a tutor asks 100 students to complete
a maths test. The tutor wants to know why some students perform
better than others. Whilst the tutor does not know the answer to
this, she thinks that it might be because of two reasons: (1) some
students spend more time revising for their test; and (2) some
students are naturally more intelligent than others. As such, the
tutor decides to investigate the effect of revision time and
intelligence on the test performance of the 100 students. The
dependent and independent variables for the study are:
Dependent Variable: Test Mark (measured from 0 to
100)
Independent Variables: Revision time (measured in
hours) Intelligence (measured using IQ score)
The dependent variable is simply that, a variable
that is dependent on an independent variable(s). For example, in our
case the test mark that a student achieves is dependent on revision
time and intelligence. Whilst revision time and intelligence (the
independent variables) may (or may not) cause a change in the test
mark (the dependent variable), the reverse is implausible; in other
words, whilst the number of hours a student spends revising and the
higher a student's IQ score may (or may not) change the test mark
that a student achieves, a change in a student's test mark has no
bearing on whether a student revises more or is more intelligent
(this simply doesn't make sense).
Therefore, the aim of the tutor's investigation is
to examine whether these independent variables - revision time and IQ
- result in a change in the dependent variable, the students' test
scores. However, it is also worth noting that whilst this is the main
aim of the experiment, the tutor may also be interested to know if
the independent variables - revision time and IQ - are also connected
in some way.
In the section on experimental and
non-experimental research that follows, we find out a little more
about the nature of independent and dependent variables.
Experimental and Non-Experimental Research
Experimental research: In experimental research, the aim is to manipulate an independent variable(s) and then examine the effect that this change has on a dependent variable(s). Since it is possible to manipulate the independent variable(s), experimental research has the advantage of enabling a researcher to identify a cause and effect between variables. For example, take our example of 100 students completing a maths exam where the dependent variable was the exam mark (measured from 0 to 100) and the independent variables were revision time (measured in hours) and intelligence (measured using IQ score). Here, it would be possible to use an experimental design and manipulate the revision time of the students. The tutor could divide the students into two groups, each made up of 50 students. In "group one", the tutor could ask the students not to do any revision. Alternately, "group two" could be asked to do 20 hours of revision in the two weeks prior to the test. The tutor could then compare the marks that the students achieved.
Non-experimental research: In non-experimental
research, the researcher does not manipulate the independent
variable(s). This is not to say that it is impossible to do so, but
it will either be impractical or unethical to do so. For example, a
researcher may be interested in the effect of illegal, recreational
drug use (the dependent variable(s)) on certain types of behaviour
(the independent variable(s)). However, whilst possible, it would be
unethical to ask individuals to take illegal drugs in order to study
what effect this had on certain behaviours. As such, a researcher
could ask both drug and non-drug users to complete a questionnaire
that had been constructed to indicate the extent to which they
exhibited certain behaviours. Whilst it is not possible to identify
the cause and effect between the variables, we can still examine the
association or relationship between them.In addition to understanding
the difference between dependent and independent variables, and
experimental and non-experimental research, it is also important to
understand the different characteristics amongst variables. This is
discussed next.
Categorical and Continuous Variables
Categorical variables are also known as discrete or qualitative variables. Categorical variables can be further categorized as either nominal, ordinal or dichotomous.
Nominal variables are variables that have
two or more categories but which do not have an intrinsic order. For
example, a real estate agent could classify their types of property
into distinct categories such as houses, condos, co-ops or bungalows.
So "type of property" is a nominal variable with 4
categories called houses, condos, co-ops and bungalows. Of note, the
different categories of a nominal variable can also be referred to as
groups or levels of the nominal variable. Another example of a
nominal variable would be classifying where people live in Karnataka
by district. In this case there will be many more levels of the
nominal variable (30 in fact).
Dichotomous variables are nominal
variables which have only two categories or levels. For example, if
we were looking at gender, we would most probably categorize somebody
as either "male" or "female". This is an example
of a dichotomous variable (and also a nominal variable). Another
example might be if we asked a person if they owned a mobile phone.
Here, we may categorise mobile phone ownership as either "Yes"
or "No". In the real estate agent example, if type of
property had been classified as either residential or commercial then
"type of property" would be a dichotomous variable.
Ordinal variables are variables that have
two or more categories just like nominal variables only the
categories can also be ordered or ranked. So if you asked someone if
they liked the policies of the Democratic Party and they could answer
either "Not very much", "They are OK" or "Yes,
a lot" then you have an ordinal variable. Why? Because you have
3 categories, namely "Not very much", "They are OK"
and "Yes, a lot" and you can rank them from the most
positive (Yes, a lot), to the middle response (They are OK), to the
least positive (Not very much). However, whilst we can rank the
levels, we cannot place a "value" to them; we cannot say
that "They are OK" is twice as positive as "Not very
much" for example.
Continuous variables are also known as
quantitative variables. Continuous variables can be further
categorized as either interval or ratio variables.
Interval variables are variables for which
their central characteristic is that they can be measured along a
continuum and they have a numerical value (for example, temperature
measured in degrees Celsius or Fahrenheit). So the difference between
20C and 30C is the same as 30C to 40C. However, temperature measured
in degrees Celsius or Fahrenheit is NOT a ratio variable.
Ratio variables are interval variables but
with the added condition that 0 (zero) of the measurement indicates
that there is none of that variable. So, temperature measured in
degrees Celsius or Fahrenheit is not a ratio variable because 0C does
not mean there is no temperature. However, temperature measured in
Kelvin is a ratio variable as 0 Kelvin (often called absolute zero)
indicates that there is no temperature whatsoever. Other examples of
ratio variables include height, mass, distance and many more. The
name "ratio" reflects the fact that you can use the ratio
of measurements. So, for example, a distance of ten metres is twice
the distance of 5 metres.
Ambiguities in classifying a type of variable
In some cases, the measurement scale for data is ordinal but the variable is treated as continuous. For example, a Likert scale that contains five values - strongly agree, agree, neither agree nor disagree, disagree, and strongly disagree - is ordinal. However, where a Likert scale contains seven or more value - strongly agree, moderately agree, agree, neither agree nor disagree, disagree, moderately disagree, and strongly disagree - the underlying scale is sometimes treated as continuous although where you should do this is a cause of great dispute.
Enrichment Activities
Central tendency
Introduction
A measure of central tendency is a single value that attempts to describe a set of data by identifying the central position within that set of data. As such, measures of central tendency are sometimes called measures of central location. They are also classed as summary statistics. The mean (often called the average) is most likely the measure of central tendency that you are most familiar with, but there are others, such as, the median and the mode.
The mean, median and mode are all valid measures
of central tendency but, under different conditions, some measures of
central tendency become more appropriate to use than others. In the
following sections we will look at the mean, mode and median and
learn how to calculate them and under what conditions they are most
appropriate to be used.
Objectives
- Understand and know that a measure of central tendency is a single value that attempts to describe a set of data by identifying the central position within that set of data.
- Understand that the mean, median and mode are all valid measures of central tendency but, under different conditions, some measures of central tendency become more appropriate to use than others.
- Learn to calculation of mean and median and analyse data and make conclusions.
Mean (Arithmetic)
The mean (or average) is the most popular and well
known measure of central tendency. It can be used with both discrete
and continuous data, although its use is most often with continuous
data. The mean is equal to the sum of all the values in the data set
divided by the number of values in the data set. So, if we have n
values in a data set and they have values x1, x2,
..., xn, then the sample mean, usually denoted by
![]() (pronounced x bar), is:
(pronounced x bar), is:
This formula is usually written in a slightly
different manner using the Greek capitol letter, Σ,
pronounced "sigma", which means "sum of...":
You may have noticed that the above formula refers
to the sample mean. So, why call have we called it a sample mean?
This is because, in statistics, samples and populations have very
different meanings and these differences are very important, even if,
in the case of the mean, they are calculated in the same way. To
acknowledge that we are calculating the population mean and not the
sample mean, we use the Greek lower case letter "mu",
denoted as µ:
The mean is essentially a model of your data set.
It is the value that is most common. You will notice, however, that
the mean is not often one of the actual values that you have observed
in your data set. However, one of its important properties is that it
minimises error in the prediction of any one value in your data set.
That is, it is the value that produces the lowest amount of error
from all other values in the data set.
An important property of the mean is that it
includes every value in your data set as part of the calculation. In
addition, the mean is the only measure of central tendency where the
sum of the deviations of each value from the mean is always zero.
When not to use the mean
The mean has one main disadvantage: it is
particularly susceptible to the influence of outliers. These are
values that are unusual compared to the rest of the data set by being
especially small or large in numerical value. For example, consider
the wages of staff at a factory below:
|
Staff
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Salary
|
15k
|
18k
|
16k
|
14k
|
15k
|
15k
|
12k
|
17k
|
90k
|
95k
|
The mean salary for these ten staff is $30.7k. However, inspecting the raw data suggests that this mean value might not be the best way to accurately reflect the typical salary of a worker, as most workers have salaries in the $12k to 18k range. The mean is being skewed by the two large salaries. Therefore, in this situation we would like to have a better measure of central tendency. As we will find out later, taking the median would be a better measure of central tendency in this situation.
Another time when we usually prefer the median
over the mean (or mode) is when our data is skewed (i.e. the
frequency distribution for our data is skewed). If we consider the
normal distribution - as this is the most frequently assessed in
statistics - when the data is perfectly normal then the mean, median
and mode are identical. Moreover, they all represent the most typical
value in the data set. However, as the data becomes skewed the mean
loses its ability to provide the best central location for the data
as the skewed data is dragging it away from the typical value.
However, the median best retains this position and is not as strongly
influenced by the skewed values. This is explained in more detail in
the skewed distribution section later in this guide.
Median
The median is the middle score for a set of data that has been arranged in order of magnitude. The median is less affected by outliers and skewed data. In order to calculate the median, suppose we have the data below:
|
65
|
55
|
89
|
56
|
35
|
14
|
56
|
55
|
87
|
45
|
92
|
We first need to rearrange that data into order of
magnitude (smallest first):
|
14
|
35
|
45
|
55
|
55
|
56
|
56
|
65
|
87
|
89
|
92
|
Our median mark is the middle mark - in this case
56 (highlighted in bold). It is the middle mark because there are 5
scores before it and 5 scores after it. This works fine when you have
an odd number of scores but what happens when you have an even number
of scores? What if you had only 10 scores? Well, you simply have to
take the middle two scores and average the result. So, if we look at
the example below:
|
65
|
55
|
89
|
56
|
35
|
14
|
56
|
55
|
87
|
45
|
We again rearrange that data into order of
magnitude (smallest first):
|
14
|
35
|
45
|
55
|
55
|
56
|
56
|
65
|
87
|
89
|
92
|
Only now we have to take the 5th and 6th score in
our data set and average them to get a median of 55.5.
Mode
The mode is the most frequent score in our data set. On a histogram it represents the highest bar in a bar chart or histogram. You can, therefore, sometimes consider the mode as being the most popular option. An example of a mode is presented below:
Normally, the mode is used for categorical data where we wish to know which is the most common category as illustrated below:
We can see above that the most common form of
transport, in this particular data set, is the bus. However, one of
the problems with the mode is that it is not unique, so it leaves us
with problems when we have two or more values that share the highest
frequency, such as below:
We are now stuck as to which mode best describes the central tendency of the data. This is particularly problematic when we have continuous data, as we are more likely not to have any one value that is more frequent than the other. For example, consider measuring 30 peoples' weight (to the nearest 0.1 kg). How likely is it that we will find two or more people with exactly the same weight, e.g. 67.4 kg? The answer, is probably very unlikely - many people might be close but with such a small sample (30 people) and a large range of possible weights you are unlikely to find two people with exactly the same weight, that is, to the nearest 0.1 kg. This is why the mode is very rarely used with continuous data.
Another problem with the mode is that it will not
provide us with a very good measure of central tendency when the most
common mark is far away from the rest of the data in the data set, as
depicted in the diagram below:
In the above diagram the mode has a value of 2. We can clearly see, however, that the mode is not representative of the data, which is mostly concentrated around the 20 to 30 value range. To use the mode to describe the central tendency of this data set would be misleading.
Skewed Distributions and the Mean and Median
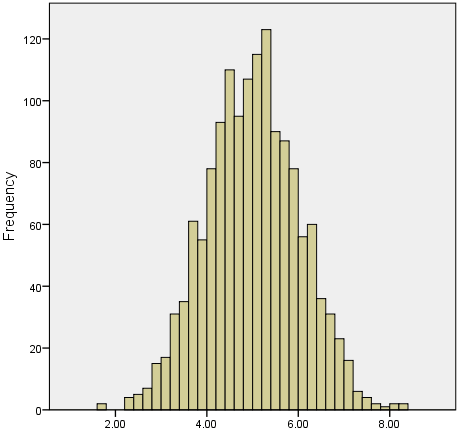 We
often test whether our data is normally distributed as this is a
common assumption underlying many statistical tests. An example of a
normally distributed set of data is presented below:
We
often test whether our data is normally distributed as this is a
common assumption underlying many statistical tests. An example of a
normally distributed set of data is presented below:
When you have a normally distributed sample you
can legitimately use both the mean or the median as your measure of
central tendency. In fact, in any symmetrical distribution the mean,
median and mode are equal. However, in this situation, the mean is
widely preferred as the best measure of central tendency as it is the
measure that includes all the values in the data set for its
calculation, and any change in any of the scores will affect the
value of the mean. This is not the case with the median or mode.
However, when our data is skewed, for example, as
with the right-skewed data set below:
we find that the mean is being dragged in the direct of the skew. In these situations, the median is generally considered to be the best representative of the central location of the data. The more skewed the distribution the greater the difference between the median and mean, and the greater emphasis should be placed on using the median as opposed to the mean. A classic example of the above right-skewed distribution is income (salary), where higher-earners provide a false representation of the typical income if expressed as a mean and not a median.
If dealing with a normal distribution, and tests
of normality show that the data is non-normal, then it is customary
to use the median instead of the mean. This is more a rule of thumb
than a strict guideline however. Sometimes, researchers wish to
report the mean of a skewed distribution if the median and mean are
not appreciably different (a subjective assessment) and if it allows
easier comparisons to previous research to be made.
Summary of when to use the mean, median and mode
Please use the following summary table to know what the best measure of central tendency is with respect to the different types of variables.
|
Type of Variable
|
Best measure of central tendency
|
|
Nominal
|
Mode
|
|
Ordinal
|
Median
|
|
Interval/Ratio (not skewed)
|
Mean
|
|
Interval/Ratio (skewed)
|
Median
|
Relative advantages and disadvantages of mean, median and mode
Mean. Advantages: Finds the most accurate average of the set of numbers. Disadvantages: Outliers (few values are very different from most) can change the mean a lot... making it much lower/higher than it should be.
Median: Advantages: Finds the middle number of a set of data, so outliers have little or no effect. Disadvantages: If the gap between some numbers is large, while it is small between other numbers in the data, this can cause the median to be a very inaccurate way to find the middle of a set of values.
Mode: Advantages: Allows you to see what value happened the most in a set of data. This can help you to figure out things in a different way. It is also quick and easy. Disadvantages: Could be very far from the actual middle of the data. The least reliable way to find the middle or average of the data.
This means that each of these measures can be useful in different kinds of distributions.
Activities
Activity 1 : Central Tendency
Learning Objectives
Learn to calculate each average measure - Mean, Median, Mode. And understand the difference between them. Know in which situation which measure must be used.
Pre-requisites/ Instructions
Materials and Resources Required
Paper and Pencil
Method
Solve the problems A and B
A. 27 members of a
class were given a puzzle to solve and the times (in minutes) each
pupil took to solve it were noted.
|
the times (in minutes) each pupil took
|
|
19 14 15 9 18 16 10 11 16
|
- The MEAN value of a set of data is Sum of Values / Number of Values . What is the mean (to 2 decimal places) of the times given in the table?
- The MEDIAN is the middle value of an ordered set of data.
- Write down the times in the table above in ascending order.
- How many values are there?
- What is the median ?
- The MODE is the value which occurs most often, i.e. the most popular.
- What is the mode of the times in the table above?
- Which of the three measures do you think is most representative of the average time? In this case it is probably the mean, but this will not always be so.
B Choosing which measure to use
The sales in one week of a particular dress are
given in terms of the dress sizes.
- Determine the mean, median and mode for this data .
- What is the size that is sold the most ?
- Which of these measures is of most use?
Dress sizes sold in one week
|
10
|
14
|
12
|
16
|
18
|
Evaluation
- Does the student understand the difference between Mean, Median and Mode
- Can the student calculate each of the measures ?
- Does the student know which measure is useful and represents the actual data given a data set ?
Self-Evaluation
Further Explorations
Enrichment Activities
Dispersion
Introduction
A measure of spread, sometimes also called a measure of dispersion, is used to describe the variability in a sample or population. It is usually used in conjunction with a measure of central tendency, such as, the mean or median, to provide an overall description of a set of data.
There are many reasons why the measure of the
spread of data values is important but one of the main reasons
regards its relationship with measures of central tendency. A measure
of spread gives us an idea of how well the mean, for example,
represents the data. If the spread of values in the data set is large
then the mean is not as representative of the data as if the spread
of data is small. This is because a large spread indicates that there
are probably large differences between individual scores.
Additionally, in research, it is often seen as positive if there is
little variation in each data group as it indicates that the similar.
We will be looking at the range, quartiles,
variance, absolute deviation and standard deviation.
Objectives
- Understand that a measure of dispersion is a measure of spread, is used to describe the variability in a sample or population.
- It is usually used in conjunction with a measure of central tendency, such as, the mean or median, to provide an overall description of a set of data.
- It important to measure the spread of data because we can understand its relationship with measures of central tendency to make more accurate interpretation of data.
- Understand and know the terms:Range, Quartile, Standard Deviation , Cumulative Frequency
- Calculation of Co-efficient of Variation. Meaning and interpretation of C.V. Analyse data and make conclusions
Range
The range is the difference between the highest and lowest scores in a data set and is the simplest measure of spread. So we calculate range as:
Range = maximum value - minimum value
For example, let us consider the following data
set:
23 56 45 65 59 55 62 54 85 25
The maximum value is 85 and the minimum value is
23. This results in a range of 62, which is 85 minus 23. Whilst using
the range as a measure of spread is limited, it does set the
boundaries of the scores. This can be useful if you are measuring a
variable that has either a critical low or high threshold (or both)
that should not be crossed. The range will instantly inform you
whether at least one value broke these critical thresholds. In
addition, the range can be used to detect any errors when entering
data. For example, if you have recorded the age of school children in
your study and your range is 7 to 123 years old you know you have
made a mistake!
Quartiles and Interquartile Range
Quartiles tell us about the spread of a data set by breaking the data set into quarters, just like the median breaks it in half. For example, consider the marks of the 100 students below, which have been ordered from the lowest to the highest scores, and the quartiles highlighted in red.
Order Score Order Score Order Score Order
Score Order Score
1st 35 21st 42 41st 53 61st 64 81st 74
2nd 37 22nd 42 42nd 53 62nd 64 82nd 74
3rd 37 23rd 44 43rd 54 63rd 65 83rd 74
4th 38 24th 44 44th 55 64th 66 84th 75
5th 39 25th 45 45th 55 65th 67 85th 75
6th 39 26th 45 46th 56 66th 67 86th 76
7th 39 27th 45 47th 57 67th 67 87th 77
8th 39 28th 45 48th 57 68th 67 88th 77
9th 39 29th 47 49th 58 69th 68 89th 79
10th 40 30th 48 50th 58 70th 69 90th 80
11th 40 31st 49 51st 59 71st 69 91st 81
12th 40 32nd 49 52nd 60 72nd 69 92nd 81
13th 40 33rd 49 53rd 61 73rd 70 93rd 81
14th 40 34th 49 54th 62 74th 70 94th 81
15th 40 35th 51 55th 62 75th 71 95th 81
16th 41 36th 51 56th 62 76th 71 96th 81
17th 41 37th 51 57th 63 77th 71 97th 83
18th 42 38th 51 58th 63 78th 72 98th 84
19th 42 39th 52 59th 64 79th 74 99th 84
20th 42 40th 52 60th 64 80th 74 100th 85
The first quartile (Q1) lies between the 25th and
26th student's marks, the second quartile (Q2) between the 50th and
51st student's marks, and the third quartile (Q3) between the 75th
and 76th student's marks. Hence:
First quartile (Q1) = 45 + 45 ÷ 2 = 45
Second quartile (Q2) = 58 + 59 ÷ 2 = 58.5
Third quartile (Q3) = 71 + 71 ÷ 2 = 71
In the above example, we have an even number of
scores (100 students rather than an odd number such as 99 students).
This means that when we calculate the quartiles, we take the sum of
the two scores around each quartile and then half them (hence Q1= 45
+ 45 ÷ 2 = 45) . However, if we had an odd number of scores (say, 99
students), then we would only need to take one score for each
quartile (that is, the 25th, 50th and 75th scores). You should
recognize that the second quartile is also the median.
Quartiles are a useful measure of spread because
they are much less affected by outliers or a skewed data set than the
equivalent measures of mean and standard deviation. For this reason,
quartiles are often reported along with the median as the best choice
of measure of spread and central tendency, respectively, when dealing
with skewed and/or data with outliers. A common way of expressing
quartiles is as an interquartile range. The interquartile range
describes the difference between the third quartile (Q3) and the
first quartile (Q1), telling us about the range of the middle half of
the scores in the distribution. Hence, for our 100 students:
Interquartile range = Q3 - Q1
= 71 - 45
= 26
However, it should be noted that in journals and
other publications you will usually see the interquartile range
reported as 45 to 71, rather than the calculated range.
A slight variation on this is the
semi-interquartile range, which is half the interquartile range = ½
(Q3 - Q1). Hence, for our 100 students, this would be 26 ÷ 2 = 13.
Standard Deviation
The standard deviation is a measure of the spread of scores within a set of data. Usually, we are interested in the standard deviation of a population. However, as we are often presented with data from a sample only, we can estimate the population standard deviation from a sample standard deviation. These two standard deviations, sample and population standard deviations, are calculated differently. In statistics we are usually presented with having to calculate sample standard deviations, and so this is what this article will focus on, although the formula for a population standard deviation will also be shown.
When to use the sample or population standard deviation
We are normally interested in knowing the population standard deviation as our population contains all the values we are interested in. Therefore, you would normally calculate the population standard deviation if: (1) you have the entire population or (2) you have a sample of a larger population but you are only interested in this sample and do not wish to generalize your findings to the population. However, in statistics, we are usually presented with a sample from which we wish to estimate (generalize to) a population, and the standard deviation is no exception to this. Therefore, if all you have is a sample but you wish to make a statement about the population standard deviation from which the sample is drawn, then you need to use the sample standard deviation. Confusion can often arise as to which standard deviation to use due to the name "sample" standard deviation incorrectly being interpreted as meaning the standard deviation of the sample itself and not as the estimate of the population standard deviation based on the sample.
What type of data should you use when you calculate a standard deviation?
The standard deviation is used in conjunction with the mean, to summarise continuous data not categorical data. In addition, the standard deviation, like the mean, is normally only appropriate when the continuous data is not significantly skewed or has outliers.
Examples of when to use the sample or population standard deviation
Q. A teacher sets an exam for their pupils. The teacher wants to summarize the results the pupils attained as a mean and standard deviation. Which standard deviation should be used?
A. Population standard deviation. Why? Because the
teacher is only interested in this class of pupils' scores and nobody
else.
Q. A researcher has recruited males aged 45 to 65
years old for an exercise training study to investigate risk markers
for heart disease, e.g. cholesterol. Which standard deviation would
most likely be used?
A. Sample standard deviation. Although not
explicitly stated, a researcher investigating health related issues
will not be simply concerned with just the participants of their
study; they will want to show how their sample results can be
generalised to the whole population (in this case, males aged 45 to
65 years old). Hence, the use of the sample standard deviation.
Q. One of the questions on a national consensus
survey asks for respondent's age. Which standard deviation would be
used to describe the variation in all ages received from the
consensus?
A. Population standard deviation. A national
consensus is used to find out information about the nation's
citizens. By definition, it includes the whole population, therefore,
a population standard deviation would be used.
What are the formulas for the standard deviation?
The sample standard deviation formula is:
where,
s = sample standard
deviation
Σ = sum
of...
X = sample mean
n = number of scores in sample.
The population standard deviation
formula is:
where,
σ
= population standard deviation
Σ
= sum of...
μ =
population mean
n = number of scores in sample.
Variation
Quartiles are useful but they are also somewhat limited because they do not take into account every score in our group of data. To get a more representative idea of spread we need to take into account the actual values of each score in a data set. The absolute deviation, variance and standard deviation are such measures.
The absolute and mean absolute deviation show the
amount of deviation (variation) that occurs around the mean score. To
find the total variability in our group of data, we simply add up the
deviation of each score from the mean. The average deviation of a
score can then be calculated by dividing this total by the number of
scores. How we calculate the deviation of a score from the mean
depends on our choice of statistic, whether we use absolute
deviation, variance or standard deviation.
Absolute Deviation and Mean Absolute Deviation
Perhaps the simplest way of calculating the deviation of a score from the mean is to take each score and minus the mean score. For example, the mean score for the group of 100 students we used earlier was 58.75 out of 100. Therefore, if we took a student that scored 60 out of 100, the deviation of a score from the mean is 60 - 58.75 = 1.25. It is important to note that scores above the mean have positive deviations (as demonstrated above) whilst that scores below the mean will have negative deviations.
To find out the total variability in our data set,
we would perform this calculation for all of the 100 students'
scores. However, the problem is that because we have both positive
and minus signs, when we add up all of these deviations, they cancel
each other out, giving us a total deviation of zero. Since we are
only interested in the deviations of the scores and not whether they
are above or below the mean score, we can ignore the minus sign and
take only the absolute value, giving us the absolute deviation.
Adding up all of these absolute deviations and dividing them by the
total number of scores then gives us the mean absolute deviation (see
below). Therefore, for our 100 students the mean absolute deviation
is 12.81, as shown below:
Variance
Another method for calculating the deviation of a group of scores from the mean, such as the 100 students we used earlier, is to use the variance. Unlike the absolute deviation, which uses the absolute value of the deviation in order to "rid itself" of the negative values, the variance achieves positive values by squaring each of the deviations instead. Adding up these squared deviations gives us the sum of squares, which we can then divide by the total number of scores in our group of data (in other words, 100 because there are 100 students) to find the variance (see below). Therefore, for our 100 students, the variance is 211.89, as shown below:
As a measure of variability, the variance is
useful. If the scores in our group of data are spread out then the
variance will be a large number. Conversely, if the scores are spread
closely around the mean, then the variance will be a smaller number.
However, there are two potential problems with the variance. First,
because the deviations of scores from the mean are 'squared', this
gives more weight to extreme scores. If our data contains outliers
(in other words, one or a small number of scores that are
particularly far away from the mean and perhaps do not represent well
our data as a whole) this can give undo weight to these scores.
Secondly, the variance is not in the same units as the scores in our
data set: variance is measured in the units squared. This means we
cannot place it on our frequency distribution and cannot directly
relate its value to the values in our data set. Therefore, the figure
of 211.89, our variance, appears somewhat arbitrary. Calculating the
standard deviation rather than the variance rectifies this problem.
Nonetheless, analysing variance is extremely important in some
statistical analyses, discussed in other statistical guides.
Coefficient of variation
Coefficient of variation is defined as
where v is the standard
deviation and x is the mean of the given data. It is also called as
a relative standard
deviation.
Remarks
- The coefficient of variation helps us to compare the consistency of two or more
- collections of data.
- When the coefficient of variation is more, the given data is less consistent.
- When the coefficient of variation is less, the given data is more consistent.
Self-Evaluation
Further Explorations
Enrichment Activities
See Also
Statistics on Wikipedia [[1]]
A
social Science statistical free and open source statistical software
[[2]]
Teachers Corner
Books
"How to lie with statistics" by Darrell Huff, Pelican, ISBN 0 14 021300 7
"Use and abuse of statistics" by W.
Reichmann, Pelican , ISBN 0 14 020707 4
"Figuring and society" by Ronald Meek,
Fontana ISBN 0 00 632560