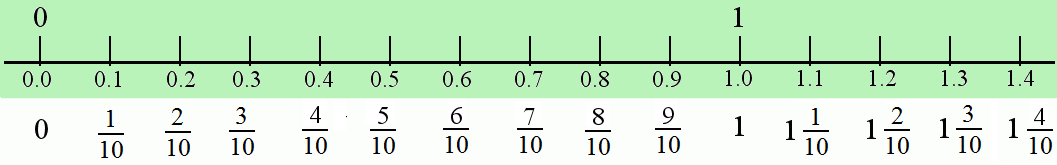Difference between revisions of "Fractions"
KOER admin (talk | contribs) (Created page with "'''Scope of this document''' <br> <br> The following is a background literature for teachers. It summarises the things to be known to a teacher to teach this topic more ...") |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| + | = Introduction = | ||
| − | The following is a | + | The following is a background literature for teachers. It |
| − | background literature for teachers. It summarises the | + | summarises the various concepts, approaches to be known to a teacher |
| − | known to a teacher to teach this topic | + | to teach this topic effectively . This literature is meant to be a |
| − | literature is meant to be a ready reference for the teacher to | + | ready reference for the teacher to develop the concepts, inculcate |
| − | develop the concepts, inculcate necessary skills, and impart | + | necessary skills, and impart knowledge in fractions from Class 6 to |
| − | knowledge in fractions from Class 6 to Class 10. | + | Class 10. |
| − | It is a well known fact | + | It is a well known fact that teaching and learning fractions is a |
| − | that teaching and learning fractions is a complicated process in | + | complicated process in primary and middle school. Although much of |
| − | primary and middle school. Although much of fractions is covered in | + | fractions is covered in the middle school, if the foundation is not |
| − | the middle school, if the foundation is not holistic and conceptual, | + | holistic and conceptual, then topics in high school mathematics |
| − | then topics in high school mathematics become very tough to grasp. | + | become very tough to grasp. Hence this documents is meant to |
| − | Hence this documents is meant to understand the research that has | + | understand the research that has been done towards simplifying and |
| − | been done towards simplifying and conceptually understanding topics | + | conceptually understanding topics of fractions. |
| − | of fractions. | + | |
| + | |||
| + | |||
| + | = Mind Map = | ||
| + | |||
| + | [[Image:KOER%20Fractions_html_m700917.png]] | ||
| − | + | = Different Models for interpreting and teaching-learning fractions = | |
| − | for | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | == Introduction == | ||
| − | + | Commonly fractions are always approached by teaching it through | |
| − | are always approached by teaching it through one model or | + | one model or interpretation namely the '''part-whole '''model |
| − | interpretation namely the '''part-whole '''model | ||
where the '''whole '''is | where the '''whole '''is | ||
divided into equal parts and the fraction represents one or more | divided into equal parts and the fraction represents one or more | ||
of the parts. The limitations of this method, especially in | of the parts. The limitations of this method, especially in | ||
explaining mixed fractions, multiplication and division of fractions | explaining mixed fractions, multiplication and division of fractions | ||
| − | + | has led to educators using other interpretations such as '''equal | |
| − | '''equal share''' and | + | share''' and '''measure'''. |
| − | '''measure'''. These | + | These approaches to fraction teaching are discussed here. |
| − | approaches to fraction teaching are discussed. | ||
| − | + | == Objectives == | |
| − | + | ||
| − | + | The objective of this section is to | |
| − | + | enable teachers to visualise and interpret fractions in different | |
| − | + | ways in order to clarify the concepts of fractions using multiple | |
| + | methods. The idea is for teachers to be able to select the | ||
| + | appropriate method depending on the context, children and class they | ||
| + | are teaching to effectively understand fractions. | ||
| − | + | == Part-whole == | |
| − | + | ||
| − | |||
| − | + | The | |
| − | + | most commonly used model is the part whole model where where the | |
| − | + | '''whole '''is | |
| − | + | divided into <u>equal</u> | |
| − | + | parts and the fraction represents one or more of the parts. | |
| − | ''' | ||
| − | + | [[Image:KOER%20Fractions_html_78a5005.gif]] | |
| − | |||
| − | + | Half | |
| − | + | (½) : The whole is divided into '''two | |
| − | + | equal '''parts. | |
| − | + | One part is coloured, this part | |
| − | + | represents the fraction ½. | |
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_6fbd7fa5.gif]] | |
| − | + | One-Fourth | |
| − | + | (1/4) : The whole is divided into '''four | |
| + | equal '''parts. | ||
| − | + | One part is coloured, this part represents the fraction ¼. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_43b75d3a.gif]] | |
| − | + | One | |
| − | ''' | + | (2/2 or 1) : The whole is divided into '''two |
| + | equal '''parts. | ||
| − | + | '''Two''' | |
| + | part are coloured, this part represents the fraction 2/2 | ||
| − | + | which is equal to the whole or 1. | |
| − | |||
| − | + | [[Image:KOER%20Fractions_html_2faaf16a.gif]] | |
| − | + | Two | |
| − | + | Fifth (2/5) : The whole is divided into '''five | |
| + | equal '''parts. | ||
| − | + | '''Two''' | |
| + | part are coloured, this part represents the fraction 2/5. | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_9e5c77.gif]]Three | |
| + | Seventh (3/7) : The whole is divided into '''seven | ||
| + | equal '''parts. | ||
| − | + | '''Three''' | |
| + | part are coloured, this part represents the fraction 3/7. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_m30791851.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Seven | |
| + | tenth (7/10) : The whole is divided into '''ten | ||
| + | equal '''parts. | ||
| − | + | '''Seven''' | |
| − | + | part are coloured, this part represents the fraction 7/10 . | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | + | '''Terms Numerator | |
| − | + | and Denominator and their meaning''' | |
| − | + | [[Image:KOER%20Fractions_html_3bf1fc6d.gif]] | |
| − | |||
| − | + | Three | |
| − | + | Eight (3/8) The whole is divided into '''eight | |
| − | ''' | + | equal '''parts. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Three''' | |
| − | ''' | + | part are coloured, this part represents the fraction 3/8 . |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 3/8 is also written as | |
| − | + | numerator/denominator. Here the number above the line- numerator | |
| − | + | tells us '''HOW MANY PARTS''' are involved. It 'enumerates' or | |
| + | counts the coloured parts. | ||
| − | + | The number '''BELOW''' the line tells – denominator tells us | |
| − | + | '''WHAT KIND OF PARTS''' the whole is divided into. It 'denominates' | |
| + | or names the parts. | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | The important factor to note here is '''WHAT IS THE WHOLE . '''In | |
| − | + | both the figures below the fraction quantity is 1/4. In fig 1 one | |
| + | circle is the whole and in fig 2, 4 circles is the whole. | ||
| − | + | [[Image:KOER%20Fractions_html_1683ac7.gif]] | |
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_729297ef.gif]][[Image:KOER%20Fractions_html_4282c1e5.gif]][[Image:KOER%20Fractions_html_6fbd7fa5.gif]] | |
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | + | == Equal Share == | |
| − | + | ||
| − | + | In the equal share interpretation the fraction '''m/n''' denotes | |
| + | one share when '''m identical things''' are '''shared equally among | ||
| + | n'''. The relationships between fractions are arrived at by logical | ||
| + | reasoning (Streefland, 1993). For example ''' 5/6 '''is the share of | ||
| + | one child when 5 rotis (disk-shaped handmade bread) are shared | ||
| + | equally among 6 children. The sharing itself can be done in more than | ||
| + | one way and each of them gives us a relation between fractions. If we | ||
| + | first distribute 3 rotis by dividing each into two equal pieces and | ||
| + | giving each child one piece each child gets 1⁄2 roti. Then the | ||
| + | remaining 2 rotis can be distributed by dividing each into three | ||
| + | equal pieces giving each child a piece. This gives us the relations | ||
| + | |||
| + | |||
| + | [[Image:KOER%20Fractions_html_3176e16a.gif]] | ||
| − | + | ||
| − | + | ||
| − | + | The relations 3/6 = 1⁄2 and 2/6 = 1/3 also follow from the | |
| − | The | + | process of distribution. Another way of distributing the rotis would |
| − | + | be to divide the first roti into 6 equal pieces give one piece each | |
| − | + | to the 6 children and continue this process with each of the | |
| + | remaining 4 rotis. Each child gets a share of rotis from each of the | ||
| + | 5 rotis giving us the relation | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_m39388388.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | It is important to note here that the fraction symbols on both | |
| − | + | sides of the equation have been arrived at simply by a repeated | |
| + | application of the share interpretation and not by appealing to prior | ||
| + | notions one might have of these fraction symbols. In the share | ||
| + | interpretation of fractions, unit fractions and improper fractions | ||
| + | are not accorded a special place. | ||
| − | + | Also converting an improper fraction to a mixed fraction becomes | |
| − | + | automatic. 6/5 is the share that one child gets when 6 rotis are | |
| − | + | shared equally among 5 children and one does this by first | |
| + | distributing one roti to each child and then sharing the remaining 1 | ||
| + | roti equally among 5 children giving us the relation | ||
| − | + | [[Image:KOER%20Fractions_html_m799c1107.gif]] | |
| − | |||
| − | |||
| − | + | Share interpretation does not provide a direct method to answer | |
| − | + | the question ‘how much is the given unknown quantity’. To say | |
| − | + | that the given unknown quantity is 3⁄4 of the whole, one has figure | |
| + | out that four copies of the given quantity put together would make | ||
| + | three wholes and hence is equal to one share when these three wholes | ||
| + | are shared equally among 4. '''''Share interpretation is also the | ||
| + | quotient interpretation of fractions in the sense that 3⁄4 = 3 ÷ 4 | ||
| + | and this is important for developing students’ ability to solve | ||
| + | problems involving multiplicative and linear functional relations. ''''' | ||
| − | + | ||
| − | + | ||
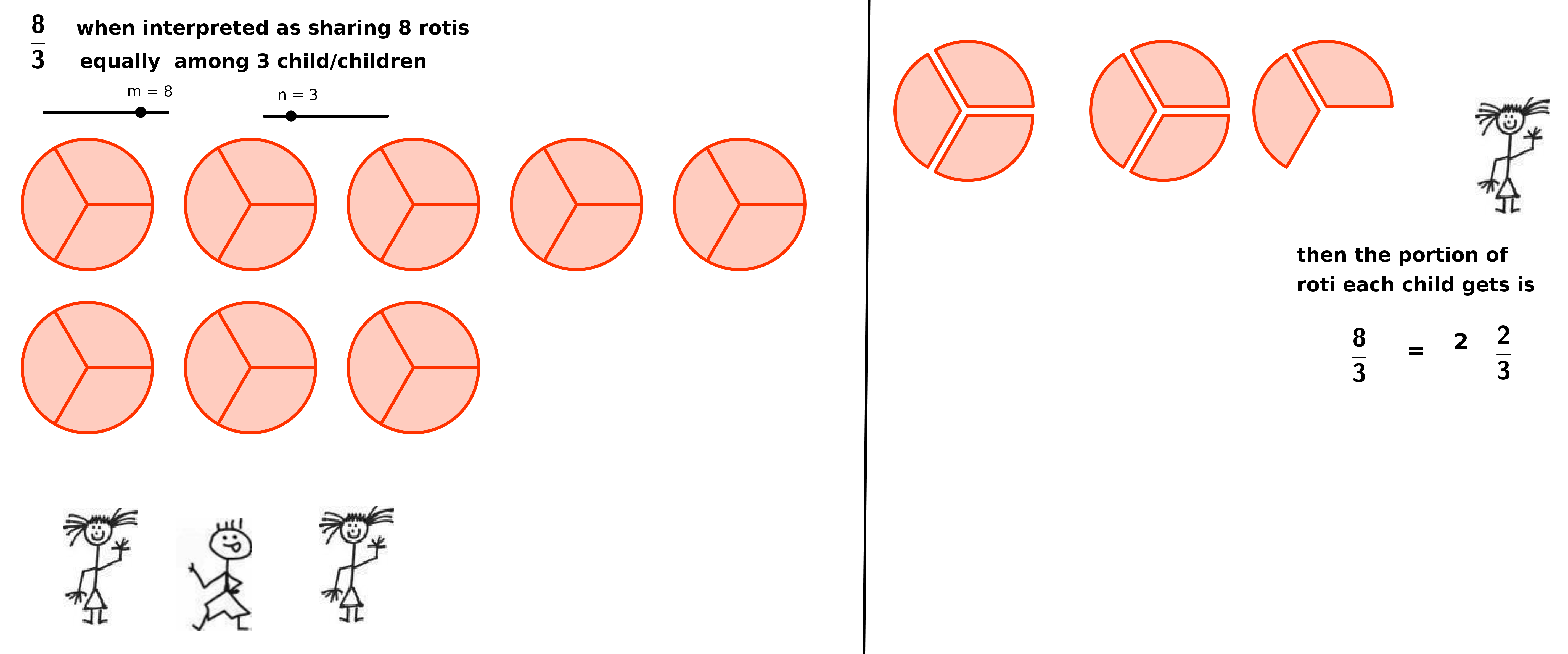
| − | + | To understand the | |
| − | + | equal share model better, use the GeoGebra file explaining the equal | |
| − | + | share model available on [[http://rmsa.karnatakaeducation.org]]. | |
| + | See figure below. Move the sliders m and n and see how the equal | ||
| + | share model is interpreted. | ||
| − | + | [[Image:KOER%20Fractions_html_17655b73.png]] | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| + | |||
| + | |||
| + | |||
| + | == Measure Model == | ||
| − | + | Measure interpretation defines the unit fraction ''1/n ''as the | |
| − | + | measure of one part when one whole is divided into ''n ''equal | |
| + | parts. The ''composite fraction'' ''m/n '' is as the measure of | ||
| + | m such parts. Thus ''5/6 '' is made of 5 piece units of size ''1/5 | ||
| + | ''each and ''6/5 ''is made of 6 piece units of size ''1/5'' | ||
| + | each. Since 5 piece units of size make a whole, we get the relation | ||
| + | 6/5 = 1 + 1/5. | ||
| − | + | Significance of measure interpretation lies in the fact that it | |
| − | + | gives a direct approach to answer the ‘how much’ question and the | |
| − | + | real task therefore is to figure out the appropriate n so that | |
| + | finitely many pieces of size will be equal to a given quantity. In a | ||
| + | sense then, the measure interpretation already pushes one to think in | ||
| + | terms of infinitesimal quantities. Measure interpretation is | ||
| + | different from the part whole interpretation in the sense that for | ||
| + | measure interpretation we fix a certain unit of measurement which is | ||
| + | the whole and the unit fractions are sub-units of this whole. The | ||
| + | unit of measurement could be, in principle, external to the object | ||
| + | being measured. | ||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | === Introducing Fractions Using Share and Measure Interpretations === | |
| − | |||
| − | |||
| − | + | One of the major difficulties a child faces with fractions is | |
| − | + | making sense of the symbol ''m/n''. In order to facilitate | |
| − | + | students’ understanding of fractions, we need to use certain | |
| + | models. Typically we use the area model in both the measure and share | ||
| + | interpretation and use a circle or a rectangle that can be | ||
| + | partitioned into smaller pieces of equal size. Circular objects like | ||
| + | roti that children eat every day have a more or less fixed size. Also | ||
| + | since we divide the circle along the radius to make pieces, there is | ||
| + | no scope for confusing a part with the whole. Therefore it is | ||
| + | possible to avoid explicit mention of the whole when we use a | ||
| + | circular model. Also, there is no need to address the issue that no | ||
| + | matter how we divide the whole into n equal parts the parts will be | ||
| + | equal. However, at least in the beginning we need to instruct | ||
| + | children how to divide a circle into three or five equal parts and if | ||
| + | we use the circular model for measure interpretation, we would need | ||
| + | ready made teaching aids such as the circular fraction kit for | ||
| + | repeated use. | ||
| − | + | Rectangular objects (like cake) do not come in the same size and | |
| − | + | can be divided into n equal parts in more than one way. Therefore we | |
| + | need to address the issues (i) that the size of the whole should be | ||
| + | fixed (ii) that all 1⁄2’s are equal– something that children do | ||
| + | not see readily. The advantage of rectangular objects is that we | ||
| + | could use paper models and fold or cut them into equal parts in | ||
| + | different ways and hence it easy to demonstrate for example that 3/5 | ||
| + | = 6/10 using the measure interpretation . | ||
| − | + | Though we expose children to the use of both circles and | |
| − | + | rectangles, from our experience we feel circular objects are more | |
| − | + | useful when use the share interpretation as children can draw as many | |
| + | small circles as they need and since the emphasis not so much on the | ||
| + | size as in the share, it does not matter if the drawings are not | ||
| + | exact. Similarly rectangular objects would be more suited for measure | ||
| + | interpretation for, in some sense one has in mind activities such as | ||
| + | measuring the length or area for which a student has to make repeated | ||
| + | use of the unit scale or its subunits. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Activities == | |
| − | |||
| − | |||
| − | |||
| − | + | === Activity1: Introduction to fractions === | |
| − | |||
| − | |||
| − | + | '''''Learning | |
| − | + | Objectives ''''' | |
| − | |||
| − | + | Introduce | |
| − | + | fractions using the part-whole method | |
| − | + | '''''Materials and | |
| − | + | resources required ''''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # Write the Number Name and the number of the picture like the example [[Image:KOER%20Fractions_html_m1d9c88a9.gif]]Number Name = One third Number: [[Image:KOER%20Fractions_html_52332ca.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_2625e655.gif]][[Image:KOER%20Fractions_html_m685ab2.gif]][[Image:KOER%20Fractions_html_55c6e68e.gif]][[Image:KOER%20Fractions_html_mfefecc5.gif]][[Image:KOER%20Fractions_html_m12e15e63.gif]] | |
| − | |||
| − | + | ||
| − | + | Question: | |
| − | + | What is the value of the numerator and denominator in the last figure | |
| − | + | , the answer is [[Image:KOER%20Fractions_html_m2dc8c779.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # Colour the correct amount that represents the fractions | |
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_19408cb.gif]][[Image:KOER%20Fractions_html_m12e15e63.gif]][[Image:KOER%20Fractions_html_m6b49c523.gif]][[Image:KOER%20Fractions_html_m6f2fcb04.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | 7/10 3/8 | |
| − | + | 1/5 4/7 | |
| − | + | Question: | |
| − | + | Before colouring count the number of parts in each figure. What does | |
| − | + | it represent. Answer: Denominator | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # Divide the circle into fractions and colour the right amount to show the fraction | |
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | + | ||
| + | 3/5 | ||
| + | 6/7 1/3 5/8 2/5 | ||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | # Draw the Fraction and observe which is the greater fraction – observe that the parts are equal for each pair | |
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 1/3 2/3 4/5 2/5 | |
| − | + | 3/7 4/7 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |||
| + | |||
| + | # Draw the Fraction and observe which is the greater fraction – Observe that the parts are different sizes for each pair. | ||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 1/3 | |
| − | + | 1/4 1/5 1/8 | |
| − | + | 1/6 1/2 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # Solve these word problems by drawing | |
| − | + | ## Amar divided an apple into 8 equal pieces. He ate 5 pieces. He put the a other 3 in a box. What fraction did Amar eat? | |
| − | + | ## There are ten biscuits in the box. 3 are cream biscuits. 2 are salt biscuits. 4 are chocolate biscuits. 1 is a sugar biscuit. What fraction of the biscuits in the box are salt biscuits. | |
| − | + | ## Radha has 6 pencils. She gives one to Anil and he gives one to Anita. She keeps the rest. What fraction of her pencils did she give away? | |
| + | # | ||
| + | # The circles in the box represent the whole; colour the right amount to show the fraction [[Image:KOER%20Fractions_html_m78f3688a.gif]]''Hint: Half is 2 circles'' [[Image:KOER%20Fractions_html_m867c5c2.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | ||
| − | |||
| − | |||
| − | |||
| − | [[Image: | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''''Pre-requisites/ |
| − | + | Instructions Method ''''' | |
| − | |||
| − | |||
| − | |||
| − | + | Do | |
| − | + | the six different sections given in the activity sheet. For each | |
| + | section there is a discussion point or question for a teacher to ask | ||
| + | children. | ||
| + | |||
| − | + | After | |
| − | + | the activity sheet is completed, please use the evaluation questions | |
| − | + | to see if the child has understood the concept of fractions | |
| − | ''' | + | '''''Evaluation''''' |
| − | |||
| + | |||
| + | === Activity 2: Proper and Improper Fractions === | ||
| − | + | '''''Learning | |
| + | Objectives''''' | ||
| − | + | Proper and Improper Fractions | |
| − | + | '''''Materials | |
| − | + | and resources required ''''' | |
| − | |||
| − | ''' | + | # [[Image:KOER%20Fractions_html_5518d221.jpg]]If you want to understand proper fraction , example 5/6. In the equal share model , 5/6 represents the share that each child gets when 5 rotis are divided among 6 children '''equally.''' |
| − | + | ||
| + | [[Image:KOER%20Fractions_html_5e906d5b.jpg]][[Image:KOER%20Fractions_html_5518d221.jpg]] | ||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_5518d221.jpg]][[Image:KOER%20Fractions_html_5e906d5b.jpg]] | |
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_5518d221.jpg]] | |
| + | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| + | |||
| + | |||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | + | ||
| − | + | ||
| − | + | # If you want to understand improper fraction , example 8/3. In the equal share model , 8/3 represents the share that each child gets when 8 rotis are divided among 3 children equally. The child in this case will usually distribute 2 full rotis to each child and then try to divide the remaining rotis. At this point you can show the mixed fraction representation as 2 2/3 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_5e906d5b.jpg]][[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | + | ||
| − | + | [[Image:KOER%20Fractions_html_5518d221.jpg]] | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[Image: | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_55f65a3d.gif]][[Image:KOER%20Fractions_html_5518d221.jpg]] |
| + | |||
| − | + | [[Image:KOER%20Fractions_html_55f65a3d.gif]] | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Pre-requisites/ | |
| − | + | Instructions Method ''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Examples of Proper and improper | |
| − | + | fractions are given. The round disks in the figure represent rotis | |
| − | + | and the children figures represent children. Cut each roti and each | |
| − | + | child figure and make the children fold, tear and equally divide the | |
| − | + | roits so that each child figure gets equal share of roti. | |
| − | share | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''''Evaluation''''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # What happens when the numerator and denominator are the same, why ? | |
| + | # What happens when the numerator is greater than the denominator why ? How can we represent this in two ways ? | ||
| − | + | ||
| − | + | ||
| − | + | === Activity 3: Comparing Fractions === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''''Learning | |
| + | Objectives''''' | ||
| + | |||
| − | + | Comparing-Fractions | |
| − | |||
| − | + | '''''Materials | |
| − | + | and resources required ''''' | |
| + | |||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | [[http://www.superteacherworksheets.com/fractions/comparing-fractions.pdf]] | |
| + | |||
| − | + | [[http://www.superteacherworksheets.com/fractions/comparing-fractions2.pdf]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Pre-requisites/ | |
| + | Instructions Method''' | ||
| − | + | Print the | |
| − | + | document and work out the | |
| + | activity sheet | ||
| − | + | '''''Evaluation''''' | |
| − | # | + | # Does the child know the symbols '''>, <''' and '''=''' |
| − | + | # What happens to the size of the part when the denominator is different ? | |
| − | + | # Does it decrease or increase when the denominator becomes larger ? | |
| − | # | + | # Can we compare quantities when the parts are different sizes ? |
| − | # | + | # What should we do to make the sizes of the parts the same ? |
| − | |||
| + | |||
| + | |||
| + | |||
| + | === Activity 4: Equivalent Fractions === | ||
| − | + | '''''Learning | |
| + | Objectives''''' | ||
| − | + | To understand Equivalent Fractions | |
| + | |||
| − | + | '''''Materials | |
| − | + | and resources required''''' | |
| − | + | [[http://www.superteacherworksheets.com/fractions/fractions-matching-game.pdf]] | |
| + | |||
| − | + | ||
| + | |||
| + | |||
| − | + | '''Pre-requisites/ | |
| − | + | Instructions Method''' | |
| − | + | Print 10 copies | |
| − | + | of the document from pages 2 to 5 fractions-matching-game | |
| − | + | Cut the each fraction part. Play memory game as described in | |
| − | + | the document in groups of 4 children. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''''Evaluation''''' | |
| − | |||
| − | |||
| − | |||
| − | + | # What is reducing a fraction to the simplest form ? | |
| − | + | # What is GCF – Greatest Common Factor ? | |
| + | # Use the document [[simplifying-fractions.pdf]] | ||
| + | # Why are fractions called equivalent and not equal. | ||
| − | + | == Evaluation == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Self-Evaluation == | |
| − | |||
| − | + | == Further Exploration == | |
| − | + | ||
| + | == Enrichment Activities == | ||
| − | = | + | = Errors with fractions = |
| − | + | == Introduction == | |
| − | |||
| − | + | A brief | |
| − | + | understanding of the common errors that children make when it comes | |
| − | + | to fractions are addressed to enable teachers to understand the | |
| + | child's levels of conceptual understanding to address the | ||
| + | misconceptions. | ||
| − | + | == Objectives == | |
| − | |||
| − | + | When fractions are operated erroneously | |
| + | like natural numbers, i.e. treating the numerator and the | ||
| + | denominators separately and not considering the relationship between | ||
| + | the numerator and the denominator is termed as N-Distractor. For | ||
| + | example 1/3 + ¼ are added to result in 2/7. Here 2 units of the | ||
| + | numerator are added and 3 & four units of the denominator are | ||
| + | added. This completely ignores the relationship between the numerator | ||
| + | and denominator of each of the fractions. Streefland (1993) noted | ||
| + | this challenge as N-distractors and a slow-down of learning when | ||
| + | moving from the '''concrete level to the abstract level'''. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == N-Distractors == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The five levels of resistance to | |
| + | N-Distractors that a child develops are: | ||
| − | |||
| − | |||
| − | |||
| − | + | # '''''Absence of cognitive conflict:''''' The child is unable to recognize the error even when she sees the same operation performed resulting in a correct answer. The child thinks both the answers are the same in spite of different results. Eg. ½ + ½ she erroneously calculated as 2/4. But when the child by some other method, say, through manipulatives (concrete) sees ½ + ½ = 1 does not recognize the conflict. | |
| − | + | # '''''Cognitive conflict takes place: '''''The student sees a conflict when she encounters the situation described in level 1 and rejects the ½+1/2 = 2/4 solution and recognizes it as incorrect. She might still not have a method to arrive at the correct solution. | |
| + | # '''''Spontaneous refutation of N-Distractor errors:''''' The student may still make N-Distractor errors, but is able to detect the error for herself. This detection of the error may be followed by just rejection or explaining the rejection or even by a correct solution. | ||
| + | # '''''Free of N-Distractor: '''''The written work is free of N-Distractors. This could mean a thorough understanding of the methods/algorithms of manipulating fractions. | ||
| + | # '''''Resistance to N-Distractor: '''''The student is completely free (conceptually and algorithmically) of N-Distractor errors. | ||
| − | |||
| − | |||
| − | |||
| − | + | == Activities == | |
| − | |||
| − | + | == Evaluation == | |
| − | |||
| − | + | == Self-Evaluation == | |
| − | |||
| − | |||
| − | + | == Further Exploration == | |
| − | + | ||
| + | # [[www.merga.net.au/publications/counter.php?pub=pub_conf&id=1410]] A PDF Research paper titled Probing Whole Number Dominance with Fractions. | ||
| + | # [[www.merga.net.au/documents/RP512004.pdf]] A PDF research paper titled “Why You Have to Probe to Discover What Year 8 Students Really Think About Fractions ” | ||
| + | # [[http://books.google.com/books?id=Y5Skj-EA2_AC&pg=PA251&lpg=PA251&dq=streefland+fractions&source=bl&ots=aabKaciwrA&sig=DcM0mi7r1GJlTUbZVq9J0l53Lrc&hl=en&ei=0xJBTvLjJ8bRrQfC3JmyBw&sa=X&oi=book_result&ct=result&resnum=1&ved=0CBUQ6AEwAA#v=onepage&q&f=false]] A google book Fractions in realistic mathematics education: a paradigm of developmental ...By Leen Streefland | ||
| + | |||
| + | == Enrichment Activities == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | = Operations on Fractions = | |
| − | |||
| − | + | == Introduction == | |
| − | |||
| − | + | This topic introduces the different operations on fractions. When | |
| + | learners move from whole numbers to fractions, many of the operations | ||
| + | are counter intuitive. This section aims to clarify the concepts | ||
| + | behind each of the operations. | ||
| − | + | == Objectives == | |
| − | |||
| − | + | The aim of this section is to visualise and conceptually | |
| + | understand each of the operations on fractions. | ||
| − | + | == Addition and Subtraction == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Adding and | |
| + | subtracting like fractions is simple. It must be emphasised thought | ||
| + | even during this process that the parts are equal in size or quantity | ||
| + | because the denominator is the same and hence for the result we keep | ||
| + | the common denominator and add the numerators. | ||
| − | |||
| − | |||
| − | |||
| − | + | Adding and | |
| + | subtracting unlike fractions requires the child to visually | ||
| + | understand that the parts of each of the fractions are differing in | ||
| + | size and therefore we need to find a way of dividing the whole into | ||
| + | equal parts so that the parts of all of the fractions look equal. | ||
| + | Once this concept is established, the terms LCM and the methods of | ||
| + | determining them may be introduced. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | == Multiplication == |
| − | + | ||
| − | + | Multiplying a | |
| − | + | fraction by a whole number: Here the repeated addition logic of | |
| − | + | multiplying whole numbers is still valid. 1/6 multiplied by 4 is 4 | |
| − | + | times 1/6 which is equal to 4/6. | |
| − | + | ||
| − | [[Image: | + | [[Image:KOER%20Fractions_html_714bce28.gif]] |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | Multiplying a | |
| + | fraction by a fraction: In this case the child is confused as | ||
| + | repeated addition does not make sense. To make a child understand the | ||
| + | ''of operator ''we can use the | ||
| + | language and demonstrate it using the measure model and the area of | ||
| + | a rectangle. | ||
| − | |||
| − | |||
| − | |||
| − | + | The | |
| + | area of a rectangle is found by multiplying side length by side | ||
| + | length. For example, in the rectangle below, the sides are 3 units | ||
| + | and 9 units, and the area is 27 square units. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_m66ce78ea.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | + | We can apply that | |
| + | idea to fractions, too. | ||
| − | + | * The one side of the rectangle is 1 unit (in terms of length). | |
| − | + | * The other side is 1 unit also. | |
| − | + | * The whole rectangle also is ''1 square unit'', in terms of area. | |
| + | |||
| + | |||
| − | + | See figure below | |
| − | + | to see how the following multiplication can be shown. | |
| − | + | ||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_m6c9f1742.gif]] | |
| + | |||
| − | + | ||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_753005a4.gif]] | |
| + | |||
| − | + | ||
| + | |||
| − | + | ||
| + | |||
| − | + | ||
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | + | '''Remember: '''The | |
| + | two fractions to multiply represent the length of the sides, and the | ||
| + | answer fraction represents area. | ||
| + | |||
| − | + | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | |||
| + | |||
| + | == Division == | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Dividing a fraction by a whole number | |
| − | + | can be demonstrated just like division of whole numbers. When we | |
| + | divide 3/4 by 2 we can visualise it as dividing 3 parts of a whole | ||
| + | roti among 4 people. | ||
| − | + | [[Image:KOER%20Fractions_html_1f617ac8.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Here 3/4 is divided between two | |
| − | + | people. One fourth piece is split into two. Each person gets | |
| + | 1/4 and 1/8. | ||
| − | + | ||
| − | |||
| − | |||
| − | [[Image: | + | [[Image:KOER%20Fractions_html_m5f26c0a.gif]] |
| − | |||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | OR | |
| − | + | [[Image:KOER%20Fractions_html_m25efcc2e.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[Image: | ||
| − | + | Another way of solving the same | |
| − | + | problem is to split each fourth piece into 2. | |
| − | |||
| − | |||
| − | into | ||
| − | |||
| − | + | This means we change the 3/4 | |
| − | + | into 6/8. | |
| − | |||
| − | [[Image: | + | [[Image:KOER%20Fractions_html_7ed8164a.gif]] |
| − | |||
| − | + | ||
| − | |||
| − | + | When dividing a fraction by a fraction, | |
| − | + | we use the measure interpretation. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_m3192e02b.gif]] | |
| − | |||
| − | + | When we divide 2 by ¼ we ask how many | |
| − | + | times does ¼ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_m257a1863.gif]][[Image:KOER%20Fractions_html_m257a1863.gif]] | |
| − | + | ||
| + | |||
| + | '''fit into 2'''. | ||
| − | + | ||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | + | It fits in 4 times in each roti, so | |
| − | + | totally 8 times. | |
| − | |||
| − | + | ||
| − | |||
| − | + | We write it as | |
| − | + | [[Image:KOER%20Fractions_html_m390fcce6.gif]] | |
| − | |||
| − | |||
| − | |||
| + | |||
| + | |||
| + | |||
| + | == Activities == | ||
| + | |||
| + | === Activity 1 Addition of Fractions === | ||
| − | + | '''''Learning | |
| − | + | Objectives''''' | |
| − | |||
| − | + | Understand Addition of Fractions | |
| − | |||
| − | + | '''''Materials | |
| − | + | and resources required ''''' | |
| − | + | ||
| + | |||
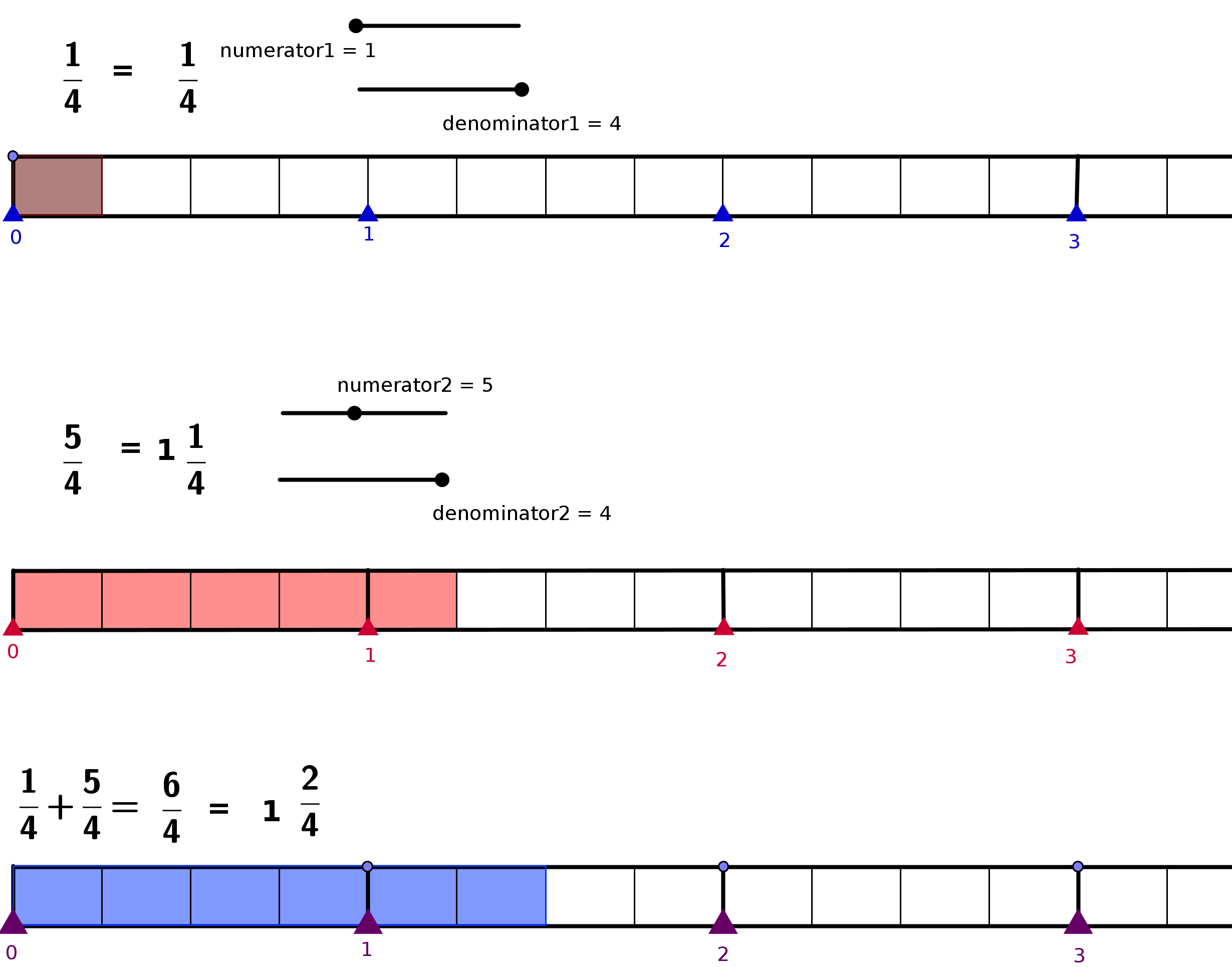
| + | [[http://rmsa.karnatakaeducation.org.in/sites/rmsa.karnatakaeducation.org.in/files/documents/Fraction_Addition.html]] | ||
| − | + | '''''Pre-requisites/ | |
| − | + | Instructions Method ''''' | |
| − | + | Open link | |
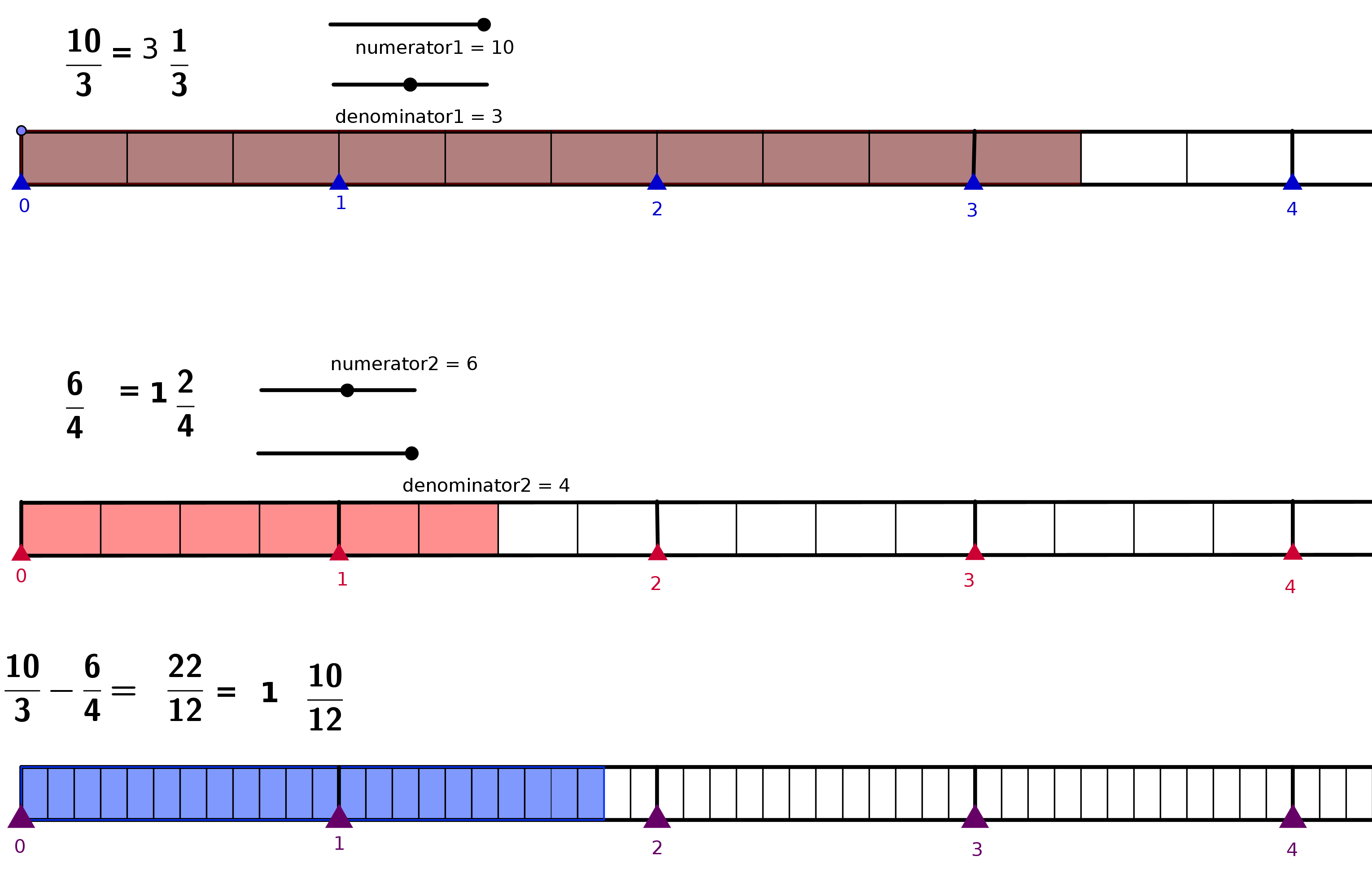
| − | + | [[http://rmsa.karnatakaeducation.org.in/sites/rmsa.karnatakaeducation.org.in/files/documents/Fraction_Addition.html]] | |
| − | |||
| − | + | [[Image:KOER%20Fractions_html_m3dd8c669.png]] | |
| − | [[Image: | + | |
| − | + | Move the sliders | |
| − | + | Numerator1 and Denominator1 to set Fraction 1 | |
| − | |||
| − | + | Move the sliders | |
| − | + | Numerator2 and Denominator2 to set Fraction 2 | |
| − | + | See the last bar | |
| − | + | to see the result of adding fraction 1 and fraction 2 | |
| − | |||
| − | + | When you move | |
| − | + | the sliders ask children to | |
| − | + | Observe and | |
| − | + | describe what happens when the denominator is changed. | |
| − | + | Observe and | |
| − | + | describe what happens when denominator changes | |
| − | |||
| − | + | Observe and | |
| − | the | + | describe the values of the numerator and denominator and relate it to |
| + | the third result fraction. | ||
| − | + | Discuss LCM and | |
| − | + | GCF | |
| − | + | ||
| + | |||
| + | '''''Evaluation''''' | ||
| + | |||
| + | === Activity 2 Fraction Subtraction === | ||
| − | + | '''''Learning | |
| − | + | Objectives ''''' | |
| − | + | Understand Fraction Subtraction | |
| + | |||
| − | + | '''''Materials and | |
| − | + | resources required''''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[http://rmsa.karnatakaeducation.org.in/sites/rmsa.karnatakaeducation.org.in/files/documents/Fraction_Subtraction.html]] | |
| − | + | ||
| + | |||
| + | '''''Pre-requisites/ | ||
| + | Instructions Method ''''' | ||
| − | + | Open link | |
| − | + | [[http://rmsa.karnatakaeducation.org.in/sites/rmsa.karnatakaeducation.org.in/files/documents/Fraction_Subtraction.html]] | |
| − | + | ||
| − | + | ||
| − | |||
| − | + | [[Image:KOER%20Fractions_html_481d8c4.png]] | |
| − | + | ||
| − | + | ||
| − | + | Move the sliders Numerator1 and Denominator1 to set Fraction 1 | |
| − | |||
| − | |||
| − | + | Move the sliders Numerator2 and Denominator2 to set Fraction 2 | |
| − | |||
| − | |||
| − | |||
| − | + | See the last bar to see the result of subtracting fraction 1 and | |
| − | + | fraction 2 | |
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | + | When you move the sliders ask children to | |
| − | |||
| − | + | observe and describe what happens when the denominator is | |
| − | + | changed. | |
| − | |||
| − | |||
| − | + | observe and describe what happens when denominator changes | |
| − | |||
| − | + | observe and describe the values of the numerator and denominator | |
| − | + | and relate it to the third result fraction. | |
| − | |||
| − | + | Discuss LCM and GCF | |
| − | |||
| − | + | '''''Evaluation''''' | |
| − | + | ||
| + | |||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === Activity 3 Multiplication of fractions === | |
| − | + | ||
| + | '''''Learning | ||
| + | Objectives ''''' | ||
| − | + | Understand Multiplication of fractions | |
| − | |||
| − | + | '''''Materials and | |
| − | + | resources required''''' | |
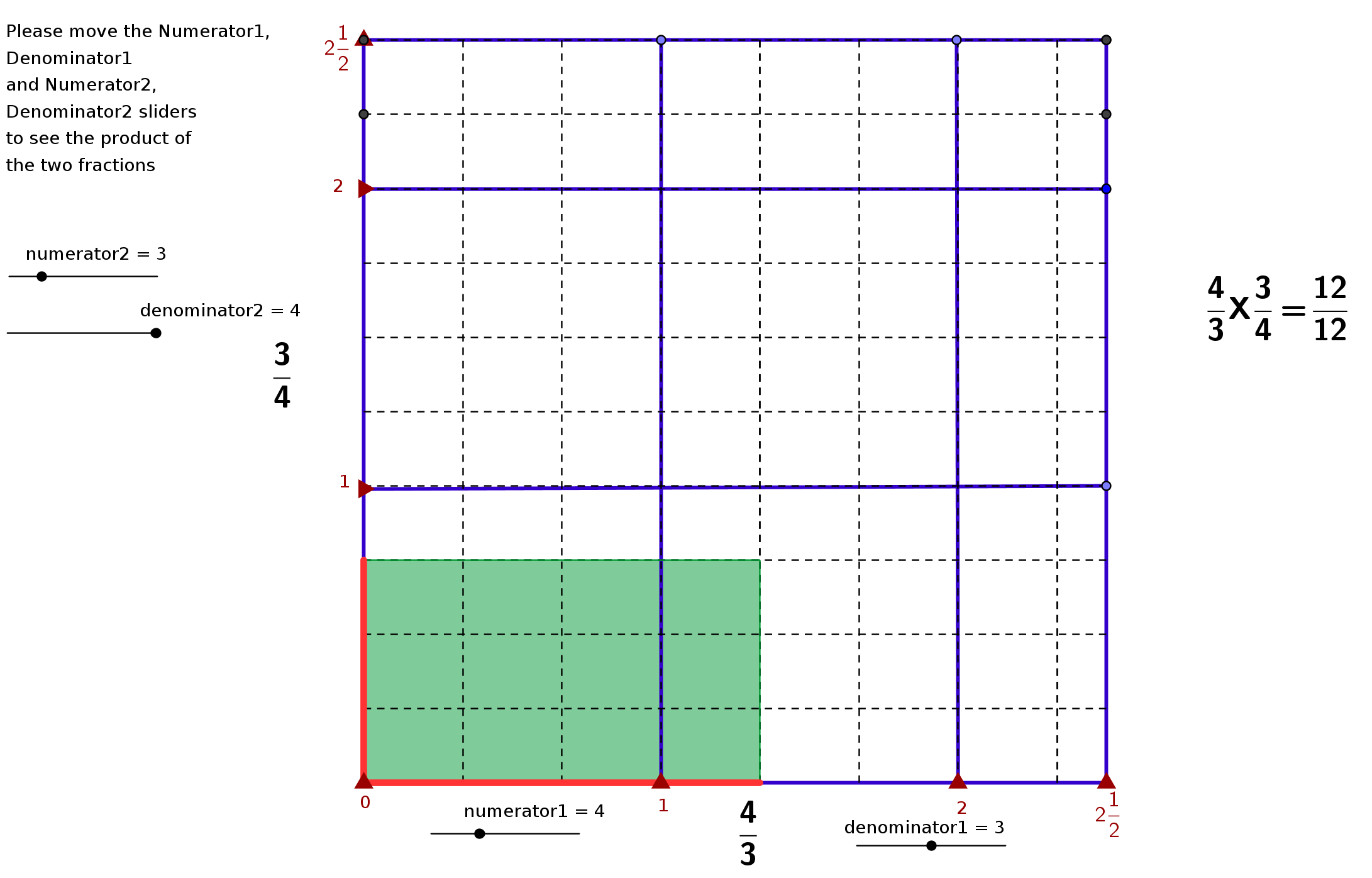
| − | + | [[http://rmsa.karnatakaeducation.org.in/sites/rmsa.karnatakaeducation.org.in/files/documents/Fraction_MultiplyArea.html]] | |
| − | |||
| − | + | '''''Pre-requisites/ | |
| − | + | Instructions Method ''''' | |
| − | + | Open link | |
| − | + | [[http://rmsa.karnatakaeducation.org.in/sites/rmsa.karnatakaeducation.org.in/files/documents/Fraction_MultiplyArea.html]] | |
| − | + | ||
| − | + | ||
| − | + | [[Image:KOER%20Fractions_html_12818756.png]] | |
| − | + | ||
| − | |||
| − | |||
| − | + | Move the sliders Numerator1 and Denominator1 to set Fraction 1 | |
| − | |||
| − | + | Move the sliders Numerator2 and Denominator2 to set Fraction 2 | |
| − | |||
| − | + | On the right hand side see the result of multiplying fraction 1 | |
| − | + | and fraction 2 | |
| − | + | '''Material/Activity Sheet''' | |
| − | |||
| − | + | Please open | |
| − | + | [[http://rmsa.karnatakaeducation.org.in/sites/rmsa.karnatakaeducation.org.in/files/documents/Fraction_MultiplyArea.html]] | |
| − | + | in Firefox and follow the process | |
| − | |||
| − | + | When you move the sliders ask children to | |
| − | |||
| − | + | observe and describe what happens when the denominator is | |
| − | + | changed. | |
| − | + | observe and describe what happens when denominator changes | |
| − | |||
| − | + | One unit will be the large square border-in blue solid lines | |
| − | |||
| − | + | A sub-unit is in dashed lines within one square unit. | |
| − | |||
| − | |||
| − | + | The thick red lines represent the fraction 1 and 2 and also the | |
| − | + | side of the quadrilateral | |
| − | + | The product represents the area of the the quadrilateral | |
| − | |||
| − | + | '''''Evaluation''''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | When | |
| − | the | + | two fractions are multiplied |
| − | + | is the product larger or smaller that the multiplicands – why ? | |
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | + | === Activity 4 Division by Fractions === | |
| − | + | ||
| + | '''''Learning | ||
| + | Objectives ''''' | ||
| − | + | Understand Division by Fractions | |
| − | |||
| − | + | '''''Materials and | |
| − | + | resources required''''' | |
| − | + | [[http://www.superteacherworksheets.com/fractions/fractionstrips_TWQWF.pdf]] | |
| − | |||
| − | |||
| − | |||
| − | + | Crayons/ colour | |
| − | + | pencils, Scissors, glue | |
| − | + | '''''Pre-requisites/ | |
| − | + | Instructions Method ''''' | |
| − | |||
| − | + | Print out the pdf | |
| − | + | [[http://www.superteacherworksheets.com/fractions/fractionstrips_TWQWF.pdf]] | |
| − | |||
| − | + | Colour each of the unit fractions in different colours. Keep the | |
| − | + | whole unit (1) white. | |
| − | |||
| − | + | Cut out each unit fraction piece. | |
| − | + | ||
| − | + | ||
| − | + | Give examples | |
| + | [[Image:KOER%20Fractions_html_m282c9b3f.gif]] | ||
| − | + | For example if we try the first one, | |
| − | + | [[Image:KOER%20Fractions_html_21ce4d27.gif]] | |
| + | See how many | ||
| + | [[Image:KOER%20Fractions_html_m31bd6afb.gif]]strips | ||
| + | will fit exactly onto whole unit strip. | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | '''''Evaluation''''' | |
| − | |||
| − | |||
| − | + | When | |
| − | + | we divide by a fraction is the result larger or smaller why ? | |
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | + | == Evaluation == | |
| − | + | ||
| − | + | == Self-Evaluation == | |
| − | + | ||
| − | + | == Further Exploration == | |
| − | + | ||
| − | + | # [[http://www.youtube.com/watch?v=41FYaniy5f8]] detailed conceptual understanding of division by fractions | |
| − | + | # [[http://www.homeschoolmath.net/teaching/f/understanding_fractions.php]] understanding fractions | |
| − | + | # [[http://www.superteacherworksheets.com]] Worksheets in mathematics for teachers to use | |
| + | |||
| + | = Linking Fractions to other Topics = | ||
| − | == | + | == Introduction == |
| − | + | It is also very common for the school system to treat themes in a | |
| − | + | separate manner. Fractions are taught as stand alone chapters. In | |
| − | + | this resource book an attempt to connect it to other middle school | |
| − | + | topics such as Ratio Proportion, Percentage and high school topics | |
| − | + | such as rational and irrational numbers, inverse proportions are | |
| − | + | made. These other topics are not discussed in detail themselves, but | |
| − | + | used to show how to link these other topics with the already | |
| − | + | understood concepts of fractions. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | + | == Objectives == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Explicitly link the other | |
| − | + | topics in school mathematics that use fractions. | |
| − | == | + | == Decimal Numbers == |
| − | + | “Decimal” | |
| − | the number | + | comes from the Latin root '''''decem''''', |
| − | + | which simply means ten. The number system we use is called the | |
| − | + | decimal number system, because the place value units go in tens: you | |
| − | + | have ones, tens, hundreds, thousands, and so on, each unit being 10 | |
| + | times the previous one. | ||
| − | + | In | |
| − | + | common language, the word “decimal number” has come to mean | |
| − | + | numbers which have digits after the decimal point, such as 5.8 or | |
| − | + | 9.302. But in reality, any number within the decimal number system | |
| − | + | could be termed a decimal number, including whole numbers such as 12 | |
| − | + | or 381. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The | |
| − | is | + | simplest way to link or connect fractions to the decimal number |
| − | + | system is with the number line representation. Any scale that a | |
| − | + | child uses is also very good for this purpose, as seen in the figure | |
| − | + | below. | |
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | The | |
| − | + | number line between 0 and 1 is divided into ten parts. Each of these | |
| + | ten parts is '''1/10''', a '''tenth'''. | ||
| − | + | [[Image:KOER%20Fractions_html_3d7b669f.gif]] | |
| − | |||
| − | [[ | ||
| − | |||
| − | |||
| − | + | Under | |
| + | the tick marks you see decimal numbers such as 0.1, 0.2, 0.3, and so | ||
| + | on. These are the same numbers as the fractions 1/10, 2/10, 3/10 and | ||
| + | so on. | ||
| − | + | We | |
| − | + | can write any fraction with '''tenths (denominator 10) '''using the | |
| − | + | decimal point. Simply write after the decimal point how many tenths | |
| − | + | the number has. 0.6 means six tenths or 1/6. 1.5 means 1 whole and 5 | |
| − | + | tenths or | |
| − | + | [[Image:KOER%20Fractions_html_m7f1d448c.gif]] | |
| − | |||
| − | |||
| − | + | Note: A common error one sees is 0.7 is written as 1 /7. It is | |
| + | seven tenths and not one seventh. That the denominator is always 10 | ||
| + | has to be stressed. To reinforce this one can use a simple rectangle | ||
| + | divided into 10 parts , the same that was used to understand place | ||
| + | value in whole numbers. | ||
| + | |||
| − | + | The | |
| − | the | + | coloured portion represents 0.6 or 6/10 and the whole block |
| − | + | represents 1. | |
| − | + | ||
| + | |||
| + | [[Image:KOER%20Fractions_html_1cf72869.gif]] | ||
| + | |||
| + | |||
| + | == Percentages == | ||
| − | + | Fractions and percentages are different ways of writing the same | |
| − | the | + | thing. When we say that a book costs Rs. 200 and the shopkeeper is |
| − | + | giving a 10 % discount. Then we can represent the 10% as a fraction | |
| + | as | ||
| + | [[Image:KOER%20Fractions_html_m1369c56e.gif]] | ||
| + | where '''10 is the numerator''' and the '''denominator is '''<u>'''always'''</u>''' | ||
| + | 100'''. In this case 10 % of the cost of the book is | ||
| + | [[Image:KOER%20Fractions_html_m50e22a06.gif]]. | ||
| + | So you can buy the book for 200 – 20 = 180 rupees. | ||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | + | There | |
| − | + | are a number of common ones that are useful to learn. Here is a table | |
| − | + | showing you the ones that you should learn. | |
| − | |||
| − | + | ||
| − | + | {| border="1" | |
| − | + | |- | |
| + | | | ||
| + | Percentage | ||
| − | + | | | |
| − | + | Fraction | |
| − | |||
| − | + | |- | |
| − | + | | | |
| + | 100% | ||
| − | + | | | |
| − | + | [[Image:KOER%20Fractions_html_m15ed765d.gif]] | |
| − | |||
| − | |||
| − | + | |- | |
| − | + | | | |
| + | 50% | ||
| − | + | | | |
| − | + | [[Image:KOER%20Fractions_html_df52f71.gif]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | |- | |
| − | + | | | |
| + | 25% | ||
| − | + | | | |
| − | + | [[Image:KOER%20Fractions_html_m6c97abb.gif]] | |
| − | |||
| − | + | |- | |
| + | | | ||
| + | 75% | ||
| − | + | | | |
| + | [[Image:KOER%20Fractions_html_m6cb13da4.gif]] | ||
| − | + | |- | |
| + | | | ||
| + | 10% | ||
| − | + | | | |
| − | + | [[Image:KOER%20Fractions_html_26bc75d0.gif]] | |
| − | + | |- | |
| + | | | ||
| + | 20% | ||
| − | + | | | |
| + | [[Image:KOER%20Fractions_html_m73e98509.gif]] | ||
| − | + | |- | |
| + | | | ||
| + | 40% | ||
| + | |||
| − | [[Image: | + | | |
| + | [[Image:KOER%20Fractions_html_m2dd64d0b.gif]] | ||
| − | + | |} | |
| + | |||
| + | |||
| − | + | ||
| + | |||
| − | + | [[Image:KOER%20Fractions_html_m60c76c68.gif]]To | |
| + | see 40 % visually see the figure : | ||
| − | + | You | |
| + | can see that if the shape is divided into 5 equal parts, then 2 of | ||
| + | those parts are shaded. | ||
| − | + | If | |
| + | the shape is divided into 100 equal parts, then 40 parts are shaded. | ||
| − | + | These | |
| − | + | are equivalent fractions as in both cases the same amount has been | |
| + | shaded. | ||
| − | + | ||
| − | + | ||
| − | + | == Ratio and Proportion == | |
| − | + | ||
| − | + | It | |
| − | + | is important to understand that fractions also can be interpreted as | |
| − | + | ratio's. Stressing that a fraction can be interpreted in many ways is | |
| − | + | of vital importance. Here briefly I describe the linkages that must | |
| − | + | be established between Ratio and Proportion and the fraction | |
| − | + | representation. Connecting multiplication of fractions is key to | |
| − | + | understanding ratio and proportion. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''What | |
| − | + | is ratio?''' | |
| − | + | Ratio | |
| − | + | is a way of comparing amounts of something. It shows how much bigger | |
| + | one thing is than another. For example: | ||
| − | + | * Use 1 measure detergent (soap) to 10 measures water | |
| − | + | * Use 1 shovel (bucket) of cement to 3 shovels (buckets) of sand | |
| − | + | * Use 3 parts blue paint to 1 part white | |
| − | + | Ratio | |
| − | + | is the number of '''parts''' to a mix. The paint mix is 4 | |
| + | parts, with 3 parts blue and 1 part white. | ||
| − | + | The | |
| − | + | order in which a ratio is stated is important. For example, the ratio | |
| + | of soap to water is 1:10. This means for every 1 measure of soap | ||
| + | there are 10 measures of water. | ||
| − | + | Mixing | |
| + | paint in the ratio 3:1 (3 parts blue paint to 1 part white paint) | ||
| + | means 3 + 1 = 4 parts in all. | ||
| + | |||
| − | + | 3 | |
| − | + | parts blue paint to 1 part white paint = is ¾ blue paint to ¼ white | |
| + | paint. | ||
| − | + | ||
| − | + | ||
| − | + | Cost | |
| − | + | of a pen is Rs 10 and cost of a pencil is Rs 2. How many times the | |
| + | cost of a pencil is the cost of a pen? Obviously it is five times. | ||
| + | This can be written as | ||
| − | + | ||
| − | + | ||
| − | + | The | |
| − | + | ratio of the cost of a pen to the cost of a pencil = | |
| + | [[Image:KOER%20Fractions_html_m762fb047.gif]] | ||
| − | + | ||
| − | + | ||
| − | + | What | |
| + | is Direct Proportion ? | ||
| + | |||
| − | + | Two | |
| − | + | quantities are in direct proportion when they increase or decrease in | |
| + | the same ratio. For example you could increase something by doubling | ||
| + | it or decrease it by halving. If we look at the example of mixing | ||
| + | paint the ratio is 3 pots blue to 1 pot white, or 3:1. | ||
| + | |||
| − | + | Paint | |
| − | + | pots in a ratio of 3:1 | |
| − | + | [[Image:KOER%20Fractions_html_m22cda036.gif]] | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | |||
| − | + | But | |
| + | this amount of paint will only decorate two walls of a room. What if | ||
| + | you wanted to decorate the whole room, four walls? You have to double | ||
| + | the amount of paint and increase it in the same ratio. | ||
| + | |||
| − | + | If | |
| − | + | we double the amount of blue paint we need 6 pots. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | If | |
| − | + | we double the amount of white paint we need 2 pots. | |
| − | |||
| − | |||
| − | + | Six | |
| − | + | paint pots in a ratio of 3:1 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The | |
| − | the | + | amount of blue and white paint we need increase in direct proportion |
| + | to each other. Look at the table to see how as you use more blue | ||
| + | paint you need more white paint: | ||
| − | + | Pots | |
| − | + | of blue paint 3 6 9 12 | |
| − | + | Pots | |
| − | + | of white paint 1 2 3 4 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Two | |
| − | + | quantities which are in direct proportion will always produce a graph | |
| − | + | where all the points can be joined to form a straight line. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''What | |
| − | + | is Inverse Proportion ?''' | |
| − | + | Two | |
| − | + | quantities may change in such a manner that if one quantity increases | |
| − | + | the the quantity decreases and vice-versa. For example if we are | |
| − | + | building a room, the time taken to finish decreases as the number of | |
| − | + | workers increase. Similarly when the speed increases the time to | |
| − | + | cover a distance decreases. Zaheeda can go to school in 4 different | |
| + | ways. She can walk, run, cycle or go by bus. | ||
| − | + | Study | |
| − | + | the table below, observe that as the speed increases time taken to | |
| − | + | cover the distance decreases | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | + | {| border="1" | |
| − | + | |- | |
| − | + | | | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | | | |
| − | + | Walk | |
| − | |||
| − | |||
| − | + | | | |
| − | + | Run | |
| − | |||
| − | + | | | |
| − | + | Cycle | |
| − | + | | | |
| + | Bus | ||
| − | + | |- | |
| + | | | ||
| + | Speed | ||
| + | Km/Hr | ||
| − | + | | | |
| + | 3 | ||
| − | + | | | |
| − | + | 6 | |
| + | (walk speed *2) | ||
| − | + | | | |
| − | + | 9 | |
| − | + | (walk speed *3) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | | | |
| − | + | 45 | |
| − | + | (walk speed *15) | |
| − | |||
| − | |||
| − | + | |- | |
| − | + | | | |
| + | Time | ||
| + | Taken (minutes) | ||
| − | + | | | |
| + | 30 | ||
| − | + | | | |
| + | 15 | ||
| + | (walk Time * ½) | ||
| − | + | | | |
| − | + | 10 | |
| + | (walk Time * 1/3) | ||
| − | + | | | |
| + | 2 | ||
| + | (walk Time * 1/15) | ||
| + | |||
| − | + | |} | |
| − | + | ||
| − | + | ||
| + | |||
| − | + | As | |
| − | + | Zaheeda doubles her speed by running, time reduces to half. As she | |
| + | increases her speed to three times by cycling, time decreases to one | ||
| + | third. Similarly, as she increases her speed to 15 times, time | ||
| + | decreases to one fifteenth. (Or, in other words the ratio by which | ||
| + | time decreases is inverse of the ratio by which the corresponding | ||
| + | speed increases). We can say that speed and time change inversely in | ||
| + | proportion. | ||
| − | + | ||
| + | |||
| + | |||
| − | + | '''Moving from Additive Thinking to | |
| + | Multiplicative Thinking ''' | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Avinash | |
| − | + | thinks that if you use 5 spoons of sugar to make 6 cups of tea, then | |
| + | you would need 7 spoons of sugar to make 8 cups of tea just as sweet | ||
| + | as the cups before. Avinash would be using an '''''additive | ||
| + | transformation''''''''; '''he thinks that since we added 2 more | ||
| + | cups of tea from 6 to 8. To keep it just as sweet he would need to | ||
| + | add to more spoons of sugar. What he does not know is that for it to | ||
| + | taste just as sweet he would need to preserve the ratio of sugar to | ||
| + | tea cup and use '''multiplicative thinking'''. He is unable to | ||
| + | detect the ratio. | ||
| − | + | === Proportional Reasoning === | |
| − | |||
| − | |||
| − | + | '''''Proportional | |
| − | + | thinking''''' involves the ability to understand and compare | |
| − | + | ratios, and to predict and produce equivalent ratios. It requires | |
| − | + | comparisons between quantities and also the relationships between | |
| − | + | quantities. It involves quantitative thinking as well as qualitative | |
| − | + | thinking. A feature of proportional thinking is the multiplicative | |
| + | relationship among the quantities and being able to recognize this | ||
| + | relationship. The relationship may be direct (divide), i.e. when one | ||
| + | quantity increases, the other also increases. The relationship is | ||
| + | inverse (multiply), when an increase in one quantity implies a | ||
| + | decrease in the other, in both cases the ratio or the rate of change | ||
| + | remains a constant. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The | |
| − | + | process of adding involved situations such as adding, joining, | |
| + | subtracting, removing actions which involves the just the two | ||
| + | quantities that are being joined, while proportional thinking is | ||
| + | associated with shrinking, enlarging, scaling , fair sharing etc. The | ||
| + | process involves multiplication. To be able to recognize, analyse and | ||
| + | reason these concepts is '''''multiplicative thinking/reasoning'''''. | ||
| + | Here the student must be able to understand the third quantity which | ||
| + | is the ratio of the two quantities. The preservation of the ratio is | ||
| + | important in the multiplicative transformation. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Rational & Irrational Numbers == | |
| − | |||
| − | |||
| − | + | After | |
| − | + | the number line was populated with natural numbers, zero and the | |
| + | negative integers, we discovered that it was full of gaps. We | ||
| + | discovered that there were numbers in between the whole numbers - | ||
| + | fractions we called them. | ||
| − | The | + | But, |
| − | the | + | soon we discovered numbers that could not be expressed as a fraction. |
| + | These numbers could not be represented as a simple fraction. These | ||
| + | were called irrational numbers. The ones that can be represented by a | ||
| + | simple fraction are called rational numbers. They h ad a very | ||
| + | definite place in the number line but all that could be said was that | ||
| + | square root of 2 is between 1.414 and 1.415. These numbers were very | ||
| + | common. If you constructed a square, the diagonal was an irrational | ||
| + | number. The idea of an irrational number caused a lot of agony to | ||
| + | the Greeks. Legend has it that Pythagoras was deeply troubled by | ||
| + | this discovery made by a fellow scholar and had him killed because | ||
| + | this discovery went against the Greek idea that numbers were perfect. | ||
| − | + | How | |
| − | + | can we be sure that an irrational number cannot be expressed as a | |
| − | + | fraction? This can be proven algebraic manipulation. Once these | |
| − | + | "irrational numbers" came to be identified, the numbers | |
| − | + | that can be expressed of the form p/q where defined as rational | |
| + | numbers. | ||
| − | + | There | |
| − | + | is another subset called transcendental numbers which have now been | |
| + | discovered. These numbers cannot be expressed as the solution of an | ||
| + | algebraic polynomial. "pi" and "e" are such | ||
| + | numbers. | ||
| − | == | + | == Activities == |
| − | === | + | === Activity 1 Fractions representation of decimal numbers === |
| − | + | '''''Learning | |
| − | + | Objectives ''''' | |
| − | + | Fractions representation of decimal | |
| + | numbers | ||
| + | |||
| − | + | '''''Materials and | |
| − | + | resources required''''' | |
| − | + | [[http://www.superteacherworksheets.com/decimals/decimal-tenths-squares_TWDWQ.pdf]] | |
| − | [[ | ||
| − | + | [[http://www.superteacherworksheets.com/decimals/decimal-hundredths-tenths.pdf]] | |
| − | |||
| − | + | ||
| − | + | ||
| − | + | '''''Pre-requisites/ | |
| − | + | Instructions Method ''''' | |
| − | + | Make copies of the worksheets | |
| − | the | + | |
| − | + | ||
| − | + | [[http://www.superteacherworksheets.com/decimals/decimal-tenths-squares_TWDWQ.pdf]] | |
| − | [[ | ||
| − | |||
| − | + | [[http://www.superteacherworksheets.com/decimals/decimal-hundredths-tenths.pdf]] | |
| − | |||
| − | |||
| − | |||
| − | + | ||
| − | |||
| − | |||
| − | + | '''''Evaluation''''' | |
| − | |||
| − | + | # Draw a number line and name the fraction and decimal numbers on the number line. Take a print of the document [[http://www.superteacherworksheets.com/decimals/decimal-number-lines-tenths.pdf]] ''' . '''Ask students to place any fraction and decimal numbers between between 0 and 10 on the number line | |
| + | # Write 0.45, 0.68, 0.05 in fraction form and represent as a fraction 100 square. | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | |||
| + | |||
| − | === | + | === Activity 2 Fraction representation and percentages === |
| − | + | '''''Learning | |
| − | + | Objectives ''''' | |
| − | + | Understand fraction representation and percentages | |
| − | |||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | + | '''''Materials and | |
| − | + | resources required''''' | |
| − | and | ||
| − | |||
| − | + | [[http://www.superteacherworksheets.com/percents/converting-fractions-decimals-percents_EASIE.pdf]] | |
| − | |||
| − | + | [[http://www.superteacherworksheets.com/percents/basic-percentages1.pdf]] | |
| − | |||
| − | ''' | + | '''''Pre-requisites/ |
| + | Instructions Method ''''' | ||
| − | + | Please print | |
| − | + | copies of the 2 activity sheets | |
| + | [[http://www.superteacherworksheets.com/percents/converting-fractions-decimals-percents_EASIE.pdf]] and | ||
| + | [[http://www.superteacherworksheets.com/percents/basic-percentages1.pdf]] and discuss the various percentage quantities with | ||
| + | the various shapes. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Then print a copy | |
| − | + | each of [[spider-percentages.pdf]] | |
| + | and make the children do this activity | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''''Evaluation''''' | |
| − | |||
| − | + | # What value is the denominator when we represent percentage as fraction ? | |
| + | # What does the numerator represent ? | ||
| + | # What does the whole fraction represent ? | ||
| + | # What other way can we represent a fraction whose denominator is 100. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | === Activity 3 === | |
| − | |||
| − | + | '''''Learning | |
| − | + | Objectives ''''' | |
| − | + | Understand fraction representation and rational and irrational | |
| + | numbers | ||
| − | + | '''''Materials and | |
| − | + | resources required''''' | |
| − | + | Thread | |
| − | + | of a certain length. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''''Pre-requisites/ | |
| − | + | Instructions Method ''''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 2,680: | Line 2,114: | ||
| − | + | ||
| Line 2,688: | Line 2,122: | ||
| − | [[Image: | + | [[Image:KOER%20Fractions_html_m1a6bd0d0.gif]] |
| Line 2,696: | Line 2,130: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Identify | Identify | ||
| − | the various places where pi, | + | the various places where pi, "e" and the golden ratio |
occur | occur | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''''Evaluation''''' | |
| − | |||
| − | + | # How many numbers can I represent on a number line between 1 and 2. | |
| + | # What is the difference between a rational and irrational number, give an example ? | ||
| + | # What is Pi ? Why is it a special number ? | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Evaluation == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Self-Evaluation == | |
| − | |||
| − | |||
| − | + | == Further Exploration == | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # Percentage and Fractions, [[http://www.bbc.co.uk/skillswise/numbers/wholenumbers/]] | |
| − | + | # A mathematical curve Koch snowflake, [[http://en.wikipedia.org/wiki/Koch_snowflake]] | |
| − | + | # Bringing it Down to Earth: A Fractal Approach, [[http://www.realmagick.com/5552/bringing-it-down-to-earth-a-fractal-approach/]] | |
| − | + | = See Also = | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # Video on teaching fractions using the equal share method made by Eklavya an NGO based in Madhya Pradesh, India [[http://vimeo.com/22238434]] | |
| − | + | # Mathematics resources from Homi Baba Centre for Science Education , [[http://mathedu.hbcse.tifr.res.in/]] | |
| − | + | # [[http://www.geogebra.com]] Understand how to use Geogebra a mathematical computer aided tool | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | = Teachers Corner = | |
| − | |||
| − | + | = Books = | |
| − | |||
| − | + | # [[http://books.google.com/books?id=Y5Skj-EA2_AC&pg=PA251&lpg=PA251&dq=streefland+fractions&source=bl&ots=aabKaciwrA&sig=DcM0mi7r1GJlTUbZVq9J0l53Lrc&hl=en&ei=0xJBTvLjJ8bRrQfC3JmyBw&sa=X&oi=book_result&ct=result&resnum=1&ved=0CBUQ6AEwAA#v=onepage&q&f=false]] A google book Fractions in realistic mathematics education: a paradigm of developmental ...By Leen Streefland | |
| − | |||
| − | |||
| − | + | = References = | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | # Introducing Fractions Using Share and Measure Interpretations: A Report from Classroom Trials . Jayasree Subramanian, Eklavya, Hoshangabad, India and Brijesh Verma,Muskan, Bhopal, India | |
| + | # Streefland, L. (1993). “Fractions: A Realistic Approach.” In Carpenter, T.P., Fennema, E., Romberg, T.A. (Eds.), Rational Numbers: an Integration of Research. (289-325). New Jersey: Lawrence, Erlbaum Associates, Publishers. | ||
Revision as of 07:21, 7 January 2013
Introduction
The following is a background literature for teachers. It summarises the various concepts, approaches to be known to a teacher to teach this topic effectively . This literature is meant to be a ready reference for the teacher to develop the concepts, inculcate necessary skills, and impart knowledge in fractions from Class 6 to Class 10.
It is a well known fact that teaching and learning fractions is a
complicated process in primary and middle school. Although much of
fractions is covered in the middle school, if the foundation is not
holistic and conceptual, then topics in high school mathematics
become very tough to grasp. Hence this documents is meant to
understand the research that has been done towards simplifying and
conceptually understanding topics of fractions.
Mind Map
Different Models for interpreting and teaching-learning fractions
Introduction
Commonly fractions are always approached by teaching it through one model or interpretation namely the part-whole model where the whole is divided into equal parts and the fraction represents one or more of the parts. The limitations of this method, especially in explaining mixed fractions, multiplication and division of fractions has led to educators using other interpretations such as equal share and measure. These approaches to fraction teaching are discussed here.
Objectives
The objective of this section is to enable teachers to visualise and interpret fractions in different ways in order to clarify the concepts of fractions using multiple methods. The idea is for teachers to be able to select the appropriate method depending on the context, children and class they are teaching to effectively understand fractions.
Part-whole
The most commonly used model is the part whole model where where the whole is divided into equal parts and the fraction represents one or more of the parts.
Half
(½) : The whole is divided into two
equal parts.
One part is coloured, this part
represents the fraction ½.
One-Fourth
(1/4) : The whole is divided into four
equal parts.
One part is coloured, this part represents the fraction ¼.
One
(2/2 or 1) : The whole is divided into two
equal parts.
Two
part are coloured, this part represents the fraction 2/2
which is equal to the whole or 1.
Two
Fifth (2/5) : The whole is divided into five
equal parts.
Two
part are coloured, this part represents the fraction 2/5.
![]() Three
Seventh (3/7) : The whole is divided into seven
equal parts.
Three
Seventh (3/7) : The whole is divided into seven
equal parts.
Three
part are coloured, this part represents the fraction 3/7.
Seven tenth (7/10) : The whole is divided into ten equal parts.
Seven
part are coloured, this part represents the fraction 7/10 .
Terms Numerator and Denominator and their meaning
Three
Eight (3/8) The whole is divided into eight
equal parts.
Three part are coloured, this part represents the fraction 3/8 .
3/8 is also written as numerator/denominator. Here the number above the line- numerator tells us HOW MANY PARTS are involved. It 'enumerates' or counts the coloured parts.
The number BELOW the line tells – denominator tells us
WHAT KIND OF PARTS the whole is divided into. It 'denominates'
or names the parts.
The important factor to note here is WHAT IS THE WHOLE . In
both the figures below the fraction quantity is 1/4. In fig 1 one
circle is the whole and in fig 2, 4 circles is the whole.
In the equal share interpretation the fraction m/n denotes one share when m identical things are shared equally among n. The relationships between fractions are arrived at by logical reasoning (Streefland, 1993). For example 5/6 is the share of one child when 5 rotis (disk-shaped handmade bread) are shared equally among 6 children. The sharing itself can be done in more than one way and each of them gives us a relation between fractions. If we first distribute 3 rotis by dividing each into two equal pieces and giving each child one piece each child gets 1⁄2 roti. Then the remaining 2 rotis can be distributed by dividing each into three equal pieces giving each child a piece. This gives us the relations
The relations 3/6 = 1⁄2 and 2/6 = 1/3 also follow from the
process of distribution. Another way of distributing the rotis would
be to divide the first roti into 6 equal pieces give one piece each
to the 6 children and continue this process with each of the
remaining 4 rotis. Each child gets a share of rotis from each of the
5 rotis giving us the relation
It is important to note here that the fraction symbols on both
sides of the equation have been arrived at simply by a repeated
application of the share interpretation and not by appealing to prior
notions one might have of these fraction symbols. In the share
interpretation of fractions, unit fractions and improper fractions
are not accorded a special place.
Also converting an improper fraction to a mixed fraction becomes
automatic. 6/5 is the share that one child gets when 6 rotis are
shared equally among 5 children and one does this by first
distributing one roti to each child and then sharing the remaining 1
roti equally among 5 children giving us the relation
Share interpretation does not provide a direct method to answer
the question ‘how much is the given unknown quantity’. To say
that the given unknown quantity is 3⁄4 of the whole, one has figure
out that four copies of the given quantity put together would make
three wholes and hence is equal to one share when these three wholes
are shared equally among 4. Share interpretation is also the
quotient interpretation of fractions in the sense that 3⁄4 = 3 ÷ 4
and this is important for developing students’ ability to solve
problems involving multiplicative and linear functional relations.
To understand the
equal share model better, use the GeoGebra file explaining the equal
share model available on [[1]].
See figure below. Move the sliders m and n and see how the equal
share model is interpreted.
Measure Model
Measure interpretation defines the unit fraction 1/n as the measure of one part when one whole is divided into n equal parts. The composite fraction m/n is as the measure of m such parts. Thus 5/6 is made of 5 piece units of size 1/5 each and 6/5 is made of 6 piece units of size 1/5 each. Since 5 piece units of size make a whole, we get the relation 6/5 = 1 + 1/5.
Significance of measure interpretation lies in the fact that it
gives a direct approach to answer the ‘how much’ question and the
real task therefore is to figure out the appropriate n so that
finitely many pieces of size will be equal to a given quantity. In a
sense then, the measure interpretation already pushes one to think in
terms of infinitesimal quantities. Measure interpretation is
different from the part whole interpretation in the sense that for
measure interpretation we fix a certain unit of measurement which is
the whole and the unit fractions are sub-units of this whole. The
unit of measurement could be, in principle, external to the object
being measured.
One of the major difficulties a child faces with fractions is making sense of the symbol m/n. In order to facilitate students’ understanding of fractions, we need to use certain models. Typically we use the area model in both the measure and share interpretation and use a circle or a rectangle that can be partitioned into smaller pieces of equal size. Circular objects like roti that children eat every day have a more or less fixed size. Also since we divide the circle along the radius to make pieces, there is no scope for confusing a part with the whole. Therefore it is possible to avoid explicit mention of the whole when we use a circular model. Also, there is no need to address the issue that no matter how we divide the whole into n equal parts the parts will be equal. However, at least in the beginning we need to instruct children how to divide a circle into three or five equal parts and if we use the circular model for measure interpretation, we would need ready made teaching aids such as the circular fraction kit for repeated use.
Rectangular objects (like cake) do not come in the same size and
can be divided into n equal parts in more than one way. Therefore we
need to address the issues (i) that the size of the whole should be
fixed (ii) that all 1⁄2’s are equal– something that children do
not see readily. The advantage of rectangular objects is that we
could use paper models and fold or cut them into equal parts in
different ways and hence it easy to demonstrate for example that 3/5
= 6/10 using the measure interpretation .
Though we expose children to the use of both circles and
rectangles, from our experience we feel circular objects are more
useful when use the share interpretation as children can draw as many
small circles as they need and since the emphasis not so much on the
size as in the share, it does not matter if the drawings are not
exact. Similarly rectangular objects would be more suited for measure
interpretation for, in some sense one has in mind activities such as
measuring the length or area for which a student has to make repeated
use of the unit scale or its subunits.
Activities
Activity1: Introduction to fractions
Learning Objectives
Introduce
fractions using the part-whole method
Materials and
resources required
- Write the Number Name and the number of the picture like the example
 Number Name = One third Number:
Number Name = One third Number: 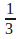
Question:
What is the value of the numerator and denominator in the last figure
, the answer is ![]()
- Colour the correct amount that represents the fractions
7/10 3/8 1/5 4/7
Question:
Before colouring count the number of parts in each figure. What does
it represent. Answer: Denominator
- Divide the circle into fractions and colour the right amount to show the fraction
3/5 6/7 1/3 5/8 2/5
- Draw the Fraction and observe which is the greater fraction – observe that the parts are equal for each pair
1/3 2/3 4/5 2/5
3/7 4/7
- Draw the Fraction and observe which is the greater fraction – Observe that the parts are different sizes for each pair.
1/3
1/4 1/5 1/8
1/6 1/2
- Solve these word problems by drawing
- Amar divided an apple into 8 equal pieces. He ate 5 pieces. He put the a other 3 in a box. What fraction did Amar eat?
- There are ten biscuits in the box. 3 are cream biscuits. 2 are salt biscuits. 4 are chocolate biscuits. 1 is a sugar biscuit. What fraction of the biscuits in the box are salt biscuits.
- Radha has 6 pencils. She gives one to Anil and he gives one to Anita. She keeps the rest. What fraction of her pencils did she give away?
- The circles in the box represent the whole; colour the right amount to show the fraction
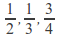 Hint: Half is 2 circles
Hint: Half is 2 circles 


Pre-requisites/
Instructions Method
Do the six different sections given in the activity sheet. For each section there is a discussion point or question for a teacher to ask children.
After
the activity sheet is completed, please use the evaluation questions
to see if the child has understood the concept of fractions
Evaluation
Activity 2: Proper and Improper Fractions
Learning Objectives
Proper and Improper Fractions
Materials
and resources required
 If you want to understand proper fraction , example 5/6. In the equal share model , 5/6 represents the share that each child gets when 5 rotis are divided among 6 children equally.
If you want to understand proper fraction , example 5/6. In the equal share model , 5/6 represents the share that each child gets when 5 rotis are divided among 6 children equally.
- If you want to understand improper fraction , example 8/3. In the equal share model , 8/3 represents the share that each child gets when 8 rotis are divided among 3 children equally. The child in this case will usually distribute 2 full rotis to each child and then try to divide the remaining rotis. At this point you can show the mixed fraction representation as 2 2/3
Pre-requisites/ Instructions Method
Examples of Proper and improper
fractions are given. The round disks in the figure represent rotis
and the children figures represent children. Cut each roti and each
child figure and make the children fold, tear and equally divide the
roits so that each child figure gets equal share of roti.
Evaluation
- What happens when the numerator and denominator are the same, why ?
- What happens when the numerator is greater than the denominator why ? How can we represent this in two ways ?
Activity 3: Comparing Fractions
Learning Objectives
Comparing-Fractions
Materials
and resources required
[[2]]
[[3]]
Pre-requisites/
Instructions Method
Print the
document and work out the
activity sheet
Evaluation
- Does the child know the symbols >, < and =
- What happens to the size of the part when the denominator is different ?
- Does it decrease or increase when the denominator becomes larger ?
- Can we compare quantities when the parts are different sizes ?
- What should we do to make the sizes of the parts the same ?
Activity 4: Equivalent Fractions
Learning Objectives
To understand Equivalent Fractions
Materials
and resources required
[[4]]
Pre-requisites/
Instructions Method
Print 10 copies
of the document from pages 2 to 5 fractions-matching-game
Cut the each fraction part. Play memory game as described in
the document in groups of 4 children.
Evaluation
- What is reducing a fraction to the simplest form ?
- What is GCF – Greatest Common Factor ?
- Use the document simplifying-fractions.pdf
- Why are fractions called equivalent and not equal.
Evaluation
Self-Evaluation
Further Exploration
Enrichment Activities
Errors with fractions
Introduction
A brief understanding of the common errors that children make when it comes to fractions are addressed to enable teachers to understand the child's levels of conceptual understanding to address the misconceptions.
Objectives
When fractions are operated erroneously like natural numbers, i.e. treating the numerator and the denominators separately and not considering the relationship between the numerator and the denominator is termed as N-Distractor. For example 1/3 + ¼ are added to result in 2/7. Here 2 units of the numerator are added and 3 & four units of the denominator are added. This completely ignores the relationship between the numerator and denominator of each of the fractions. Streefland (1993) noted this challenge as N-distractors and a slow-down of learning when moving from the concrete level to the abstract level.
N-Distractors
The five levels of resistance to N-Distractors that a child develops are:
- Absence of cognitive conflict: The child is unable to recognize the error even when she sees the same operation performed resulting in a correct answer. The child thinks both the answers are the same in spite of different results. Eg. ½ + ½ she erroneously calculated as 2/4. But when the child by some other method, say, through manipulatives (concrete) sees ½ + ½ = 1 does not recognize the conflict.
- Cognitive conflict takes place: The student sees a conflict when she encounters the situation described in level 1 and rejects the ½+1/2 = 2/4 solution and recognizes it as incorrect. She might still not have a method to arrive at the correct solution.
- Spontaneous refutation of N-Distractor errors: The student may still make N-Distractor errors, but is able to detect the error for herself. This detection of the error may be followed by just rejection or explaining the rejection or even by a correct solution.
- Free of N-Distractor: The written work is free of N-Distractors. This could mean a thorough understanding of the methods/algorithms of manipulating fractions.
- Resistance to N-Distractor: The student is completely free (conceptually and algorithmically) of N-Distractor errors.
Activities
Evaluation
Self-Evaluation
Further Exploration
- www.merga.net.au/publications/counter.php?pub=pub_conf&id=1410 A PDF Research paper titled Probing Whole Number Dominance with Fractions.
- www.merga.net.au/documents/RP512004.pdf A PDF research paper titled “Why You Have to Probe to Discover What Year 8 Students Really Think About Fractions ”
- [[5]] A google book Fractions in realistic mathematics education: a paradigm of developmental ...By Leen Streefland
Enrichment Activities
Operations on Fractions
Introduction
This topic introduces the different operations on fractions. When learners move from whole numbers to fractions, many of the operations are counter intuitive. This section aims to clarify the concepts behind each of the operations.
Objectives
The aim of this section is to visualise and conceptually understand each of the operations on fractions.
Addition and Subtraction
Adding and subtracting like fractions is simple. It must be emphasised thought even during this process that the parts are equal in size or quantity because the denominator is the same and hence for the result we keep the common denominator and add the numerators.
Adding and subtracting unlike fractions requires the child to visually understand that the parts of each of the fractions are differing in size and therefore we need to find a way of dividing the whole into equal parts so that the parts of all of the fractions look equal. Once this concept is established, the terms LCM and the methods of determining them may be introduced.
Multiplication
Multiplying a fraction by a whole number: Here the repeated addition logic of multiplying whole numbers is still valid. 1/6 multiplied by 4 is 4 times 1/6 which is equal to 4/6.
Multiplying a fraction by a fraction: In this case the child is confused as repeated addition does not make sense. To make a child understand the of operator we can use the language and demonstrate it using the measure model and the area of a rectangle.
The area of a rectangle is found by multiplying side length by side length. For example, in the rectangle below, the sides are 3 units and 9 units, and the area is 27 square units.
We can apply that idea to fractions, too.
- The one side of the rectangle is 1 unit (in terms of length).
- The other side is 1 unit also.
- The whole rectangle also is 1 square unit, in terms of area.
See figure below
to see how the following multiplication can be shown.
Remember: The
two fractions to multiply represent the length of the sides, and the
answer fraction represents area.
Division
Dividing a fraction by a whole number can be demonstrated just like division of whole numbers. When we divide 3/4 by 2 we can visualise it as dividing 3 parts of a whole roti among 4 people.
Here 3/4 is divided between two
people. One fourth piece is split into two. Each person gets
1/4 and 1/8.
OR
Another way of solving the same
problem is to split each fourth piece into 2.
This means we change the 3/4
into 6/8.
When dividing a fraction by a fraction, we use the measure interpretation.
When we divide 2 by ¼ we ask how many
times does ¼
fit into 2.
It fits in 4 times in each roti, so
totally 8 times.
Activities
Activity 1 Addition of Fractions
Learning Objectives
Understand Addition of Fractions
Materials
and resources required
[[6]]
Pre-requisites/
Instructions Method
Open link
[[7]]
Move the sliders Numerator1 and Denominator1 to set Fraction 1
Move the sliders
Numerator2 and Denominator2 to set Fraction 2
See the last bar
to see the result of adding fraction 1 and fraction 2
When you move
the sliders ask children to
Observe and
describe what happens when the denominator is changed.
Observe and
describe what happens when denominator changes
Observe and
describe the values of the numerator and denominator and relate it to
the third result fraction.
Discuss LCM and
GCF
Evaluation
Activity 2 Fraction Subtraction
Learning Objectives
Understand Fraction Subtraction
Materials and
resources required
[[8]]
Pre-requisites/
Instructions Method
Open link
[[9]]
Move the sliders Numerator1 and Denominator1 to set Fraction 1
Move the sliders Numerator2 and Denominator2 to set Fraction 2
See the last bar to see the result of subtracting fraction 1 and
fraction 2
When you move the sliders ask children to
observe and describe what happens when the denominator is
changed.
observe and describe what happens when denominator changes
observe and describe the values of the numerator and denominator
and relate it to the third result fraction.
Discuss LCM and GCF
Evaluation
Activity 3 Multiplication of fractions
Learning Objectives
Understand Multiplication of fractions
Materials and
resources required
[[10]]
Pre-requisites/
Instructions Method
Open link
[[11]]
Move the sliders Numerator1 and Denominator1 to set Fraction 1
Move the sliders Numerator2 and Denominator2 to set Fraction 2
On the right hand side see the result of multiplying fraction 1
and fraction 2
Material/Activity Sheet
Please open
[[12]]
in Firefox and follow the process
When you move the sliders ask children to
observe and describe what happens when the denominator is
changed.
observe and describe what happens when denominator changes
One unit will be the large square border-in blue solid lines
A sub-unit is in dashed lines within one square unit.
The thick red lines represent the fraction 1 and 2 and also the
side of the quadrilateral
The product represents the area of the the quadrilateral
Evaluation
When
two fractions are multiplied
is the product larger or smaller that the multiplicands – why ?
Activity 4 Division by Fractions
Learning Objectives
Understand Division by Fractions
Materials and
resources required
[[13]]
Crayons/ colour
pencils, Scissors, glue
Pre-requisites/
Instructions Method
Print out the pdf
[[14]]
Colour each of the unit fractions in different colours. Keep the
whole unit (1) white.
Cut out each unit fraction piece.
For example if we try the first one,
![]() See how many
See how many
![]() strips
will fit exactly onto whole unit strip.
strips
will fit exactly onto whole unit strip.
Evaluation
When
we divide by a fraction is the result larger or smaller why ?
Evaluation
Self-Evaluation
Further Exploration
- [[15]] detailed conceptual understanding of division by fractions
- [[16]] understanding fractions
- [[17]] Worksheets in mathematics for teachers to use
Linking Fractions to other Topics
Introduction
It is also very common for the school system to treat themes in a separate manner. Fractions are taught as stand alone chapters. In this resource book an attempt to connect it to other middle school topics such as Ratio Proportion, Percentage and high school topics such as rational and irrational numbers, inverse proportions are made. These other topics are not discussed in detail themselves, but used to show how to link these other topics with the already understood concepts of fractions.
Objectives
Explicitly link the other topics in school mathematics that use fractions.
Decimal Numbers
“Decimal” comes from the Latin root decem, which simply means ten. The number system we use is called the decimal number system, because the place value units go in tens: you have ones, tens, hundreds, thousands, and so on, each unit being 10 times the previous one.
In
common language, the word “decimal number” has come to mean
numbers which have digits after the decimal point, such as 5.8 or
9.302. But in reality, any number within the decimal number system
could be termed a decimal number, including whole numbers such as 12
or 381.
The
simplest way to link or connect fractions to the decimal number
system is with the number line representation. Any scale that a
child uses is also very good for this purpose, as seen in the figure
below.
The
number line between 0 and 1 is divided into ten parts. Each of these
ten parts is 1/10, a tenth.
Under the tick marks you see decimal numbers such as 0.1, 0.2, 0.3, and so on. These are the same numbers as the fractions 1/10, 2/10, 3/10 and so on.
We
can write any fraction with tenths (denominator 10) using the
decimal point. Simply write after the decimal point how many tenths
the number has. 0.6 means six tenths or 1/6. 1.5 means 1 whole and 5
tenths or
![]()
Note: A common error one sees is 0.7 is written as 1 /7. It is
seven tenths and not one seventh. That the denominator is always 10
has to be stressed. To reinforce this one can use a simple rectangle
divided into 10 parts , the same that was used to understand place
value in whole numbers.
The
coloured portion represents 0.6 or 6/10 and the whole block
represents 1.
Percentages
Fractions and percentages are different ways of writing the same
thing. When we say that a book costs Rs. 200 and the shopkeeper is
giving a 10 % discount. Then we can represent the 10% as a fraction
as
![]() where 10 is the numerator and the denominator is always
100. In this case 10 % of the cost of the book is
where 10 is the numerator and the denominator is always
100. In this case 10 % of the cost of the book is
![]() .
So you can buy the book for 200 – 20 = 180 rupees.
.
So you can buy the book for 200 – 20 = 180 rupees.
There
are a number of common ones that are useful to learn. Here is a table
showing you the ones that you should learn.
|
Percentage
|
Fraction
|
|
100%
|
|
|
50%
|
|
|
25%
|
|
|
75%
|
|
|
10%
|
|
|
20%
|
|
|
40%
|
|
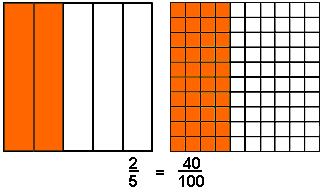 To
see 40 % visually see the figure :
To
see 40 % visually see the figure :
You
can see that if the shape is divided into 5 equal parts, then 2 of
those parts are shaded.
If
the shape is divided into 100 equal parts, then 40 parts are shaded.
These
are equivalent fractions as in both cases the same amount has been
shaded.
Ratio and Proportion
It is important to understand that fractions also can be interpreted as ratio's. Stressing that a fraction can be interpreted in many ways is of vital importance. Here briefly I describe the linkages that must be established between Ratio and Proportion and the fraction representation. Connecting multiplication of fractions is key to understanding ratio and proportion.
What
is ratio?
Ratio
is a way of comparing amounts of something. It shows how much bigger
one thing is than another. For example:
- Use 1 measure detergent (soap) to 10 measures water
- Use 1 shovel (bucket) of cement to 3 shovels (buckets) of sand
- Use 3 parts blue paint to 1 part white
Ratio is the number of parts to a mix. The paint mix is 4 parts, with 3 parts blue and 1 part white.
The
order in which a ratio is stated is important. For example, the ratio
of soap to water is 1:10. This means for every 1 measure of soap
there are 10 measures of water.
Mixing
paint in the ratio 3:1 (3 parts blue paint to 1 part white paint)
means 3 + 1 = 4 parts in all.
3
parts blue paint to 1 part white paint = is ¾ blue paint to ¼ white
paint.
Cost
of a pen is Rs 10 and cost of a pencil is Rs 2. How many times the
cost of a pencil is the cost of a pen? Obviously it is five times.
This can be written as
The
ratio of the cost of a pen to the cost of a pencil =
![]()
What
is Direct Proportion ?
Two
quantities are in direct proportion when they increase or decrease in
the same ratio. For example you could increase something by doubling
it or decrease it by halving. If we look at the example of mixing
paint the ratio is 3 pots blue to 1 pot white, or 3:1.
Paint
pots in a ratio of 3:1
But this amount of paint will only decorate two walls of a room. What if you wanted to decorate the whole room, four walls? You have to double the amount of paint and increase it in the same ratio.
If
we double the amount of blue paint we need 6 pots.
If
we double the amount of white paint we need 2 pots.
Six
paint pots in a ratio of 3:1
The
amount of blue and white paint we need increase in direct proportion
to each other. Look at the table to see how as you use more blue
paint you need more white paint:
Pots
of blue paint 3 6 9 12
Pots
of white paint 1 2 3 4
Two
quantities which are in direct proportion will always produce a graph
where all the points can be joined to form a straight line.
What
is Inverse Proportion ?
Two
quantities may change in such a manner that if one quantity increases
the the quantity decreases and vice-versa. For example if we are
building a room, the time taken to finish decreases as the number of
workers increase. Similarly when the speed increases the time to
cover a distance decreases. Zaheeda can go to school in 4 different
ways. She can walk, run, cycle or go by bus.
Study
the table below, observe that as the speed increases time taken to
cover the distance decreases
|
|
Walk
|
Run
|
Cycle
|
Bus
|
|
Speed Km/Hr
|
3
|
6 (walk speed *2)
|
9 (walk speed *3)
|
45 (walk speed *15)
|
|
Time Taken (minutes)
|
30
|
15 (walk Time * ½)
|
10 (walk Time * 1/3)
|
2 (walk Time * 1/15)
|
As
Zaheeda doubles her speed by running, time reduces to half. As she
increases her speed to three times by cycling, time decreases to one
third. Similarly, as she increases her speed to 15 times, time
decreases to one fifteenth. (Or, in other words the ratio by which
time decreases is inverse of the ratio by which the corresponding
speed increases). We can say that speed and time change inversely in
proportion.
Moving from Additive Thinking to
Multiplicative Thinking
Avinash thinks that if you use 5 spoons of sugar to make 6 cups of tea, then you would need 7 spoons of sugar to make 8 cups of tea just as sweet as the cups before. Avinash would be using an additive transformation'''; he thinks that since we added 2 more cups of tea from 6 to 8. To keep it just as sweet he would need to add to more spoons of sugar. What he does not know is that for it to taste just as sweet he would need to preserve the ratio of sugar to tea cup and use multiplicative thinking. He is unable to detect the ratio.
Proportional Reasoning
Proportional thinking involves the ability to understand and compare ratios, and to predict and produce equivalent ratios. It requires comparisons between quantities and also the relationships between quantities. It involves quantitative thinking as well as qualitative thinking. A feature of proportional thinking is the multiplicative relationship among the quantities and being able to recognize this relationship. The relationship may be direct (divide), i.e. when one quantity increases, the other also increases. The relationship is inverse (multiply), when an increase in one quantity implies a decrease in the other, in both cases the ratio or the rate of change remains a constant.
The process of adding involved situations such as adding, joining, subtracting, removing actions which involves the just the two quantities that are being joined, while proportional thinking is associated with shrinking, enlarging, scaling , fair sharing etc. The process involves multiplication. To be able to recognize, analyse and reason these concepts is multiplicative thinking/reasoning. Here the student must be able to understand the third quantity which is the ratio of the two quantities. The preservation of the ratio is important in the multiplicative transformation.
Rational & Irrational Numbers
After the number line was populated with natural numbers, zero and the negative integers, we discovered that it was full of gaps. We discovered that there were numbers in between the whole numbers - fractions we called them.
But,
soon we discovered numbers that could not be expressed as a fraction.
These numbers could not be represented as a simple fraction. These
were called irrational numbers. The ones that can be represented by a
simple fraction are called rational numbers. They h ad a very
definite place in the number line but all that could be said was that
square root of 2 is between 1.414 and 1.415. These numbers were very
common. If you constructed a square, the diagonal was an irrational
number. The idea of an irrational number caused a lot of agony to
the Greeks. Legend has it that Pythagoras was deeply troubled by
this discovery made by a fellow scholar and had him killed because
this discovery went against the Greek idea that numbers were perfect.
How
can we be sure that an irrational number cannot be expressed as a
fraction? This can be proven algebraic manipulation. Once these
"irrational numbers" came to be identified, the numbers
that can be expressed of the form p/q where defined as rational
numbers.
There
is another subset called transcendental numbers which have now been
discovered. These numbers cannot be expressed as the solution of an
algebraic polynomial. "pi" and "e" are such
numbers.
Activities
Activity 1 Fractions representation of decimal numbers
Learning Objectives
Fractions representation of decimal
numbers
Materials and
resources required
[[18]]
[[19]]
Pre-requisites/
Instructions Method
Make copies of the worksheets
[[20]]
[[21]]
Evaluation
- Draw a number line and name the fraction and decimal numbers on the number line. Take a print of the document [[22]] . Ask students to place any fraction and decimal numbers between between 0 and 10 on the number line
- Write 0.45, 0.68, 0.05 in fraction form and represent as a fraction 100 square.
Activity 2 Fraction representation and percentages
Learning Objectives
Understand fraction representation and percentages
Materials and
resources required
[[23]]
[[24]]
Pre-requisites/
Instructions Method
Please print
copies of the 2 activity sheets
[[25]] and
[[26]] and discuss the various percentage quantities with
the various shapes.
Then print a copy each of spider-percentages.pdf and make the children do this activity
Evaluation
- What value is the denominator when we represent percentage as fraction ?
- What does the numerator represent ?
- What does the whole fraction represent ?
- What other way can we represent a fraction whose denominator is 100.
Activity 3
Learning Objectives
Understand fraction representation and rational and irrational
numbers
Materials and
resources required
Thread
of a certain length.
Pre-requisites/
Instructions Method
Construct
Koch's snowflakes .
Start with a thread of a certain length (perimeter) and using the same thread construct the following shapes (see Figure).
See
how the shapes can continue to emerge but cannot be identified
definitely with the same perimeter (length of the thread).
Identify the various places where pi, "e" and the golden ratio occur
Evaluation
- How many numbers can I represent on a number line between 1 and 2.
- What is the difference between a rational and irrational number, give an example ?
- What is Pi ? Why is it a special number ?
Evaluation
Self-Evaluation
Further Exploration
- Percentage and Fractions, [[27]]
- A mathematical curve Koch snowflake, [[28]]
- Bringing it Down to Earth: A Fractal Approach, [[29]]
See Also
- Video on teaching fractions using the equal share method made by Eklavya an NGO based in Madhya Pradesh, India [[30]]
- Mathematics resources from Homi Baba Centre for Science Education , [[31]]
- [[32]] Understand how to use Geogebra a mathematical computer aided tool
Teachers Corner
Books
- [[33]] A google book Fractions in realistic mathematics education: a paradigm of developmental ...By Leen Streefland
References
- Introducing Fractions Using Share and Measure Interpretations: A Report from Classroom Trials . Jayasree Subramanian, Eklavya, Hoshangabad, India and Brijesh Verma,Muskan, Bhopal, India
- Streefland, L. (1993). “Fractions: A Realistic Approach.” In Carpenter, T.P., Fennema, E., Romberg, T.A. (Eds.), Rational Numbers: an Integration of Research. (289-325). New Jersey: Lawrence, Erlbaum Associates, Publishers.