Mensuration
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Error: Mind Map file Mensuration.mm not found
Textbook
NCERT 10 Textbook Chapter 13-Surface Areas and Volumes
Additional Information
Useful websites
- Download PDF. This is a good website for interesting activities on mensuration.
- For standard measurements : http://www.primaryresources.co.uk/maths/mathsE1.htm
- http://www.campusgate.co.in/2011/11/areas-and-mensuration.html
- For general rules while writing units ://en.wikipedia.org/wiki/International_System_of_Units#General_rules
- For teacher reference on dimension. http://www.britannica.com/EBchecked/topic/163641/dimension
- The metric system is enormously powerful as a standard measurement system. In this video, you can explore from the very small to the very large and appreciate what a degree of ten means!
Reference Books
Teaching Outlines
Concept #1. What is Mensuration ?
Learning objectives
- units and measurement
- Mensuration is the branch of Mathematics dealing with measurement of angles, length, area, and volume.
- There are standard and non-standard ways of measurements.
- Importance of having standardised measurements.
- The length of the total boundary of a figure is called its perimeter. The Metric unit of perimeter is same as the unit of length - Metre.
- The amount of surface covered by an object is called it area. The Metric unit of area is square metre.
- The capacity of an object to hold is called its volume.
- They should develop the ability to calculate the area, perimeter, volume or side of many different figures.
Notes for teachers
Source: http://depts.washington.edu/chemcrs/bulkdisk/chem120A_sum06/handout_CH%201-4%20TIMBER.pdf
Summary : Measurement are an important part of our everyday life. Think about your day; you probably made some measurements. Perhaps you checked your weight by stepping on a scale,measuring shoes to fit your feet in the shoe store, or saw measuring up houses when they are doing renovations etc. If you did not feel well, you may have taken your temperature. To make some soup, you added 2 cups of water to a package mix. If you stopped at the Petrol bunk, you watched the petrol pump measure the number of litres of petrol you put in the car.
Activity No #1
for the details of the activity 1 click below
Importance of measurements and calculations - What and why to measure?
Activity No #2
for the details of the activity 2 click below
Importance of measurements and calculations - a discussion
Concept #2.Informal units of measurements
Learning objectives
- The traditional ways of measurements are a type of measure which uses non-standard units such as hand spans, armlengths, footsteps or pattern blocks to measure length, area, etc.
- Non-standard measurements are not always the same but vary from person to person.
Notes for teachers
- The teacher can ask the students to gather information regarding earlier traditional measuring ways from their elders and have an initial discussion in the classroom.
Activity No # 1.
for the details of the activity 1 click below
Informal units of measurements
Estimating distances
- Estimated Time :1 hour
- Materials/ Resources needed : Sticks, ropes, writing pad, pencil.
- Prerequisites/Instructions, if any
- They should have the ability to measure and document their findings accurately.
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process:
- The teacher can ask the students to determine the distances of library, principal's room, playground, dining hall, entrance gate from their classroom using various non-standard measuring methods.
- The children can decide which method to use - whether foot, sticks or ropes.
- The task can be done in groups of 3 children.
- Document and compare the results.
- Discuss regarding the length of distance.
- Reiterate that it is very important to use same measuring modes to facilitate comparisons.
- Developmental Questions:
- Which point would we mark as the point of reference for measuring our classroom.
- Similarly what are the points of reference for other places.
- How do we mark them.
- Which measuring unit have you chosen ?
- How will you document the findings ?
- How can we tabulate our findings on board for comparisons ?
- What would be our report back time ?
- What are our findings ?
- What conclusions can we draw ?
- Evaluation:
- What have we learnt so far about measuring object?
- Question Corner:
- How can we measure curves?
- What are the problems with non-standard measuring units?
- Can we think of methods to measure so that measures taken by anyone would always be same for a given object or distance.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept #3. Standard units of measurements
Learning objectives
- The ability to obtain accurate measurements and communicate those measurements is a key requirement for progress.
- Standardised measuring units ensure uniformity in meaurements.
- The standard unit for length is metre, for weight id kilogram, for time is second, for temperature is Kelvin and for amount of substance it is mole.
Notes for teachers
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of measurement.
For example, length is a physical quantity. The metre is a unit of length that represents a definite predetermined length. When we say 10 metres (or 10 m), we actually mean 10 times the definite predetermined length called "metre".<br.
The definition, agreement, and practical use of units of measurement have played a crucial role in human endeavour from early ages up to this day. Different systems of units used to be very common. Now there is a global standard, the International System of Units (SI), the modern form of the metric system.
===Activity No # 1.
Hunting treasure and measuring===
- Estimated Time : 1 hour
- Materials/ Resources needed : Weighing balance, measuring tape, spring balance, digital scale, postal scale, thermometer, litre and millilitre cans.
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process:
- Let the students measure different ingredients using suitable measuring instruments and record their observations in a tabular form.
- Developmental Questions
- What did you measure ?
- What measuring instrument did you select ? Why ?
- What was your reading ?
- which unit do you use ?
- Evaluation
- Were the students able to comprehend which measuring instrument should be used for particular items ?
- Were they able to document their observations appropriately in a tabular form.
- Question Corner
- Write a note on why standard measuring units are very important.
=Activity No # 2. Hunting treasure and measuring
- Estimated Time : 1 hour
- Materials/ Resources needed:
- Weighing pan with measures of 1 kg, 500gm, 250gm and 100gm and 50gm.
- Digital scale
- Postal scale.
- Measuring cans of 1 litre, 500ml, 250 ml, 100ml,
- Measuring tape, Ruler.
- Watch or stop clock.
- Paper and pen.
- Prerequisites/Instructions, if any
- The students should have been introduced to the concept of formal measurements by conducting an activity on using standard measuring instruments.
- They should understand the importance of standard measurements and distinction between standard and non-standard units of measurements.
- They should be well versed with standard units and subunits.
- They should know unit conversions.
- They should have the skill of measuring and recording accurately.
- They should be aware that comparisons can be made only between similar measuring units.
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process:
- The idea here is to inculde several measuring units for practise.
- Initially instruct the students regarding the activity and its purpose.
- Group students into 3 in each.
- The teacher shall make packets of things as treasure and hide them in the school premises.
- The students shall pick chits containing clues to hunt and find the packets.
- 30 minutes is given to search.
- The students search packets and come back to classroom.
- The packets may contain cloth, ribbons, ropes, water, fruits, ingredients , vegetable , books , juice, stamps,envelops or any such measurable items.
- The students have to quickly decide which measuring mode they are going to use, measure and record their findings.
- They also have to measure the distance at which they found each and record the time taken to search.
- Developmental Questions:
Ask the students to write on
- What treasures did they find ?
- At what distance did they find ?
- How much time did they take to find ?
- What measuring instruments did they use ?, why ?
- How will they tabulate their results ?
- Can you list the purpose of each ?
- Evaluation
- The teacher should analyse the students skill of documentation.
- Question Corner:
- What are standard the units of length ?
- What are the standard units of weight ?
- How are liquids measured ?
Activity :Paint and fill the Cylinder
- Estimated Time: 20 minutes
- Materials/ Resources needed
- instrument box
- Hard paper
- gum tape
- paints-green and red
- brush
- Prerequisites/Instructions:
- Students are asked to cut paper into rectangular shape of any length (l) and breadth(b).
- Students are asked to cut paper into two congruent circles of circumference=length of rectangle(l)
- Students are asked to make a cylinder using rectangle and two congruent circles.
- Students are asked to use Red paint for painting single side of rectangle and circles and green for filling cylinder
- prerequisite knowledge:
- What is cylinder?
- Area of cylinder
- volume of cylinder
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process:
- Students are grouped (each group has 4 students). They are asked to calculate the area of rectangle painted and area of circles painted.
- Students are asked to find out the quantity of green paint used to fill the cylinder.
- Developmental Questions:
- which shape the rectangular paper takes when rolled?
- What is the circumference of the circle?
- What is the relation between length of rectangle and circumference of the circle?
- what is the area of rectangle?
- what is the area of circle?
- Evaluation
- Question Corner
Concept # 4. Scale drawing
Learning objectives
- The process of representing actual distances on paper using proportional distances is called a scale.
- A Scale drawing is a drawing that shows a real object with accurate sizes except they have all been reduced or enlarged by a certain amount (called the scale).
- Since it is not always possible to draw on paper the actual size of real-life objects such as the real size of a car, an airplane, we need scale drawings to represent the size.
- Drawing to scale is a tool that Engineers use for many different tasks. One key part of every scale drawing is the scaling factor. This number represents the degree to which our scale drawing or scale model has been reduced in size when compared to the original.
Notes for teachers
Activity No # 1.(Part A): Representing distances on paper-Introduction to scale drawing
- Estimated Time : 1 hour
- Materials/ Resources needed :
- Scale, pencil, graph paper.
- Prerequisites/Instructions, if any
- Skill of measuring and tabulating accurately.
- Knowledge of ratio and proportions.
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process:
- This activity can be done in groups by grouping 3 students in each.
- The students should measure distances of library, dinning hall, principal's room, entrance gate, playground etc from their class room using a measuring tape in metres.
- The teacher can mark reference points for each and explain to the students.
- The students should accurately measure and note down.
- After coming to the classroom let the teacher tabulate all distances on the blackboard.
- Next ask the students to represent their observation of distances by drawing their school model on paper.
- Ask them how will they go about it so that the distances are represented proportionately.
- The teacher can then elicit from the students that a proper equivalent unit has to be used for the purpose.
- After this activity she can spell out the term scale and discuss about the blue print of a house, mapping distances, atlas maps, model constructions and so on.
- This activity can be done to introduce the students to the concept of scale drawing.
- Developmental Questions
- What did you measure ?
- What measuring instrument did you select ? Why ?
- What was your reading ?
- which unit do you use ?
- Evaluation
- Were the students able to comprehend which measuring instrument should be used for particular items ?
- Were they taking measurements accurately ?
- Were they able to document their observations appropriately in a tabular form ?
- Question Corner:
- Discuss the applications of scale drawing ?
- What is a scale factor ?
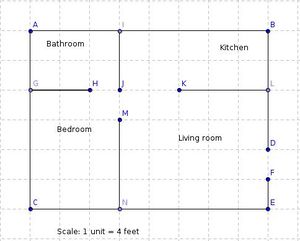
Activity No # (PART B) : Estimating Tile costs
- Estimated Time :45 minutes
- Materials/ Resources needed:
Graph sheets, scale, pencil,
- Prerequisites/Instructions, if any
- The students should have knowledge about scale drawing.
- They should know about scale factor.
- They should understand that a scaling factor should be maintained as constant throughout the sketches.
- Students should be able to read and understand a scaling factor.
- They should be able to find a scaling factor and create a scale drawing.
- The activity on using standard measuring instruments should be done prior to this activity.
- The students should have been introduced to area, calculations and unit conversions.
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process:
- In the above blue print each individual unit is 4 feet.
- Explain the meaning of 1 unit.
- Each ceramic tile costs Rs 80 per square foot.
- How much would it cost to tile the bathroom ?
- How much would it cost to tile Kitchen, Living room and bedroom?
- Developmental Questions
- Along with knowing the length and width of the scale model, what additional information do you need to know ?
- What is the scale factor here.
- Evaluation:
- What is 1 unit in the given blue print.
- What does '1 unit = 4 feet mean' ?
- What are the actual dimensions of each room ?
- Question Corner:
- What all factors do you need to know to estimate the painting costs for each of the rooms.
- Write down the sequential steps for the calculations.
Hints for difficult problems
Mensuration
Exercise 16.1
Problem 7.
1)Craft teacher of a school taught the students to prepare cylindrical pen holders out of card board. In a class of strength 42, if each child prepared a pen holder of radius 5 cm and height 14 cm, how much cardboard was consumed?
Statement of the problem:
How much cardboard was consumed to prepare 42 cylindrical pen holders each of radius 5 cm and height 14 cm.
- Interpretation;
Case 1)Pen stand which is open on top and closed base. Then we have to calculate Curved surface area of cylinder and area of one circle.
- skills
visualising the cylinder into rectangle and circle
- Assumptions:
Concepts used
- basics of circles -radius
- area of circles
- addition and multiplication of fractions
- unit of area
knowledge to be used
- knowledge of Polygons -Rectangles
- knowledge of measurements
- Formula of CSA of cylinder
- substitution
- computing
- Value of Л
Concepts to be taught
- basics of circles -radius
- area of circles
- relation between circumference of circle and length of rectangle in a cylinder
- addition and multiplication of fractions
- unit of area
solution: r=5cm, h=14cm, Л=
Curved surface area of cylinder and area of one circle= CSA of cylinder+area of circle
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2Лrh+Лr^2}
=
=440+78.5
=518.5cm
Cardboard required to prepare 42 penstands= 42X518.5
=
=
Case 2:- Hollow pen stand: Pen stand which is open both the sides i.e., top and base.
Then we have to calculate Curved surface area of cylinder.
Case 3:-Pen stand which is closed both the sides i.e., top and base.
Then we have to calculate total surface area of cylinder.
Activity Making use of 2200 cmcardboard sheet how many hollow cylinders of radius 7 cm and height 5 cm can be prepared.
solved problems on cone Example 10
- Find the weight of a solid cone whose base is of diameter 14 cm and vertical height 51,
cm, if the material of which it is made weighs 10gm/
- Statement of the problem:What is the weight of a solid cone whose base is of diameter 14 cm and vertical height 51cm, if the material of which it is made weighs 10gm/
- Interpretation;
Calculating the weight of solid cone by calculating its volume. density of a material is given. it is related to volume and weight.
- Assumptions:
Concepts used
- basics of circles -radius
- area of circles
- multiplication of fractions
- unit of volume,density and weight
- density
knowledge to be used
- radius=diameter/2
- density=mass/volume
- knowledge of measurements
- Formula of volume of cones
- substitution
- computing
- Value of Л
Concepts to be taught
- density
- units conversion
solution:
d=14cm r=7cm, h=51cm
Volume of cone=
=Failed to parse (syntax error): {\displaystyle \frac{1}{3}{Л}{r^2}h}
=
=
To calculate weight of the solid cone we have to use density of the given material.
density=
=
Weight of solid cone=volumeXdensity
=
=26.18Kg
problem on combination of solids example 01
Problem-03
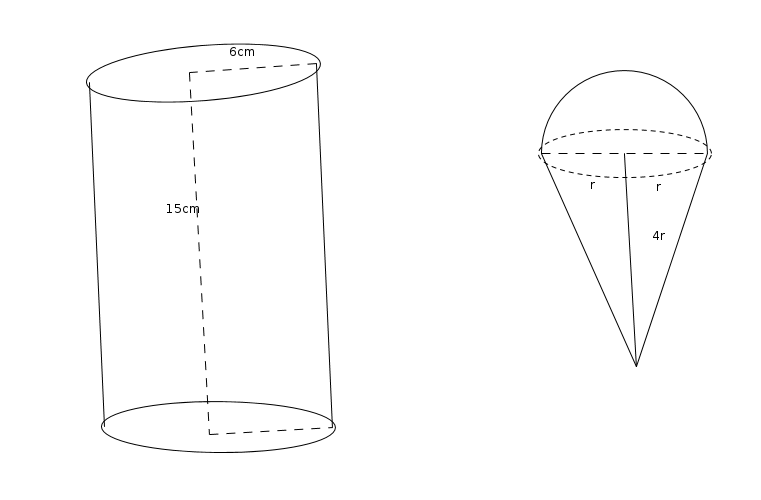
- A Cylindrical container of radius 6cm and height 15cm is filled with ice cream. The whole ice cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height
of the conical portion is 4 times the radius of its base , find the radius of the cream cones.
Solution
- Statement of the problem
- A Cylindrical container of radius 6cm and height 15cm is filled with ice cream. The whole ice cream has to be filled in 10 equal cones with hemispherical tops. and the height
of the conical portion is 4 times the radius of its base.
.
Assumptions
- Student should know volume of cone,and volume of Hemisphere
- Student should know the value of л=22/7
- Student should know the difference between radius and height
- Student should know the proper substitution simplification
Concepts to be taught
- Let us consider the volume of a cone having hemispherical top =2л
- Volume of Cylindrical container is equated to volume of cone having hemispherical top
Gaps
- Comparision between the volumes of cylinder and (cone+Hemisphere)
Skills
- To imagine a cone , Hemisphere,and cylinder
- To imagine a cone having Hemispherical top
Algorthem
Part 1:
To derive the volume of a cone with hemispherical top
- volume of a cone with hemispherical top
=Failed to parse (syntax error): {\displaystyle {\frac{1}{3}}л{r^2}h+{\frac{2}{3}}л{r^3}}
=Failed to parse (syntax error): {\displaystyle {\frac{1}{3}}л4r +{\frac{2}{3}}л{r^3}}
(on simplification)
=Failed to parse (syntax error): {\displaystyle 2л{r^3}}
Part 2 :
To calculate the volume of 10 cone with hemispherical top
=Failed to parse (syntax error): {\displaystyle 10X2л{r^3}}
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 20л{r^3}}
To calculate the volume of ice-cream in cylindrical container
=Failed to parse (syntax error): {\displaystyle л{r^2}h}
= л X6X6X15
=540лc
Part 3 :
To apply condition given in the problem
volume of 10 cone with hemispherical top= volume of cylindrical container
Failed to parse (syntax error): {\displaystyle 20л{r^3}}
=540л
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {\frac{540л}{20л}}}
=27
r=3cm
Hence the radius of cream cones=3cm
=
Project Ideas
Projects Given for the Different Groups
Students Will be divided into different groups and each group is named as cylinder,cone,pyramid etc
Group-01(cylinder)
Students of this group will be asked to make different cylinders say Hallow cylinder,Solid cylinder,cylinder with a base without top etc using cardboard.
Now Students should have to write the following
- Different properties of Cylinder
- Different formulae (LSA,TSA,VOLUME of Cylinder)
- Procedure:
- Materials used in making cylinder
- Different cuttings that they made
- Measurements of those cuttings
NOTE:
The Students of other groups will be asked to follow the same method mentioned above
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template