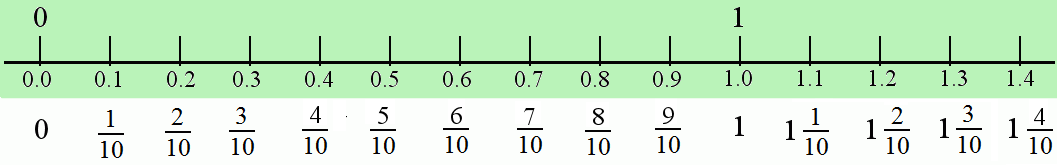Fractions

Introduction

The following is a background literature for teachers. It summarises the various concepts, approaches to be known to a teacher to teach this topic effectively . This literature is meant to be a ready reference for the teacher to develop the concepts, inculcate necessary skills, and impart knowledge in fractions from Class 6 to Class 10.

It is a well known fact that teaching and learning fractions is a complicated process in primary and middle school. Although much of fractions is covered in the middle school, if the foundation is not holistic and conceptual, then topics in high school mathematics become very tough to grasp. Hence this documents is meant to understand the research that has been done towards simplifying and conceptually understanding topics of fractions.

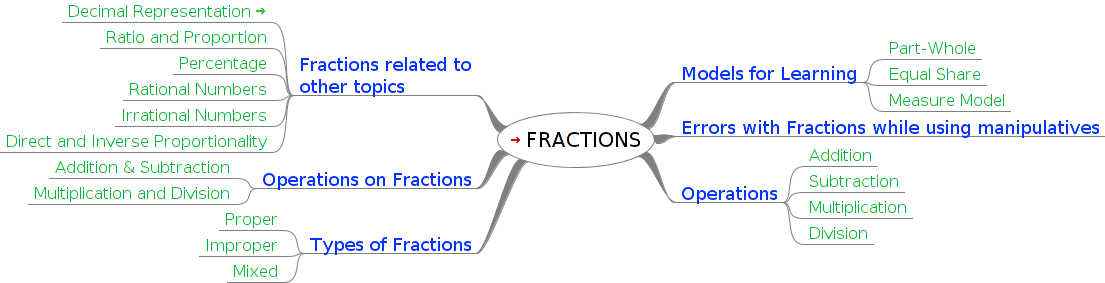
Mind Map

Different Models for interpreting and teaching-learning fractions

Introduction

Commonly fractions are always approached by teaching it through one model or interpretation namely the part-whole model where the whole is divided into equal parts and the fraction represents one or more of the parts. The limitations of this method, especially in explaining mixed fractions, multiplication and division of fractions has led to educators using other interpretations such as equal share and measure. These approaches to fraction teaching are discussed here.

Objectives

The objective of this section is to enable teachers to visualise and interpret fractions in different ways in order to clarify the concepts of fractions using multiple methods. The idea is for teachers to be able to select the appropriate method depending on the context, children and class they are teaching to effectively understand fractions.

Part-whole

The most commonly used model is the part whole model where where the whole is divided into equal parts and the fraction represents one or more of the parts.

Half (½) : The whole is divided into two equal parts.

One part is coloured, this part represents the fraction ½.

One-Fourth (1/4) : The whole is divided into four equal parts.

One part is coloured, this part represents the fraction ¼.

One (2/2 or 1) : The whole is divided into two equal parts.

Two part are coloured, this part represents the fraction 2/2

which is equal to the whole or 1.

Two Fifth (2/5) : The whole is divided into five equal parts.

Two part are coloured, this part represents the fraction 2/5.

Three Seventh (3/7) : The whole is divided into seven equal parts.

Three part are coloured, this part represents the fraction 3/7.

Seven tenth (7/10) : The whole is divided into ten equal parts.

Seven part are coloured, this part represents the fraction 7/10 .

Terms Numerator and Denominator and their meaning

Three Eight (3/8) The whole is divided into eight equal parts.

Three part are coloured, this part represents the fraction 3/8 .

3/8 is also written as numerator/denominator. Here the number above the line- numerator tells us HOW MANY PARTS are involved. It 'enumerates' or counts the coloured parts.

The number BELOW the line tells – denominator tells us WHAT KIND OF PARTS the whole is divided into. It 'denominates' or names the parts.

The important factor to note here is WHAT IS THE WHOLE . In both the figures below the fraction quantity is 1/4. In fig 1 one circle is the whole and in fig 2, 4 circles is the whole.

Equal Share

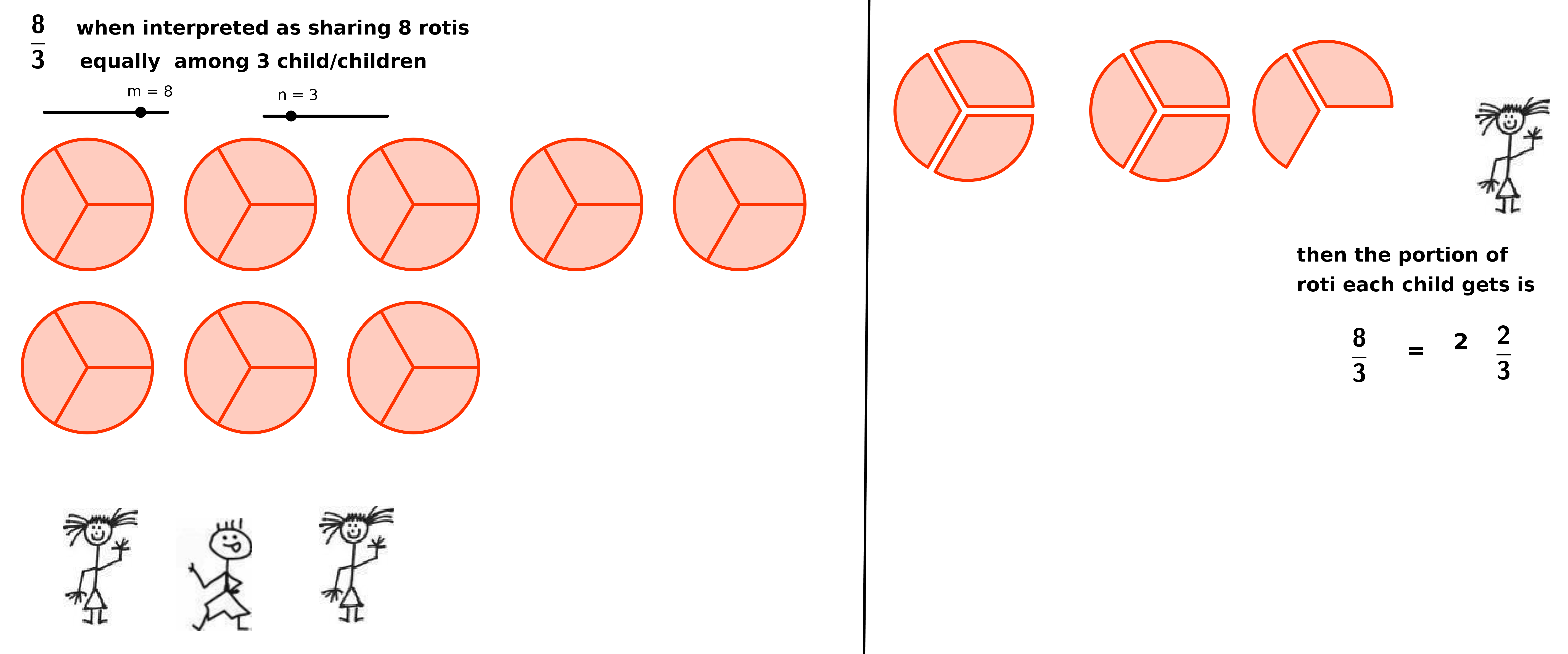
In the equal share interpretation the fraction m/n denotes one share when m identical things are shared equally among n. The relationships between fractions are arrived at by logical reasoning (Streefland, 1993). For example 5/6 is the share of one child when 5 rotis (disk-shaped handmade bread) are shared equally among 6 children. The sharing itself can be done in more than one way and each of them gives us a relation between fractions. If we first distribute 3 rotis by dividing each into two equal pieces and giving each child one piece each child gets 1⁄2 roti. Then the remaining 2 rotis can be distributed by dividing each into three equal pieces giving each child a piece. This gives us the relations

The relations 3/6 = 1⁄2 and 2/6 = 1/3 also follow from the process of distribution. Another way of distributing the rotis would be to divide the first roti into 6 equal pieces give one piece each to the 6 children and continue this process with each of the remaining 4 rotis. Each child gets a share of rotis from each of the 5 rotis giving us the relation

It is important to note here that the fraction symbols on both sides of the equation have been arrived at simply by a repeated application of the share interpretation and not by appealing to prior notions one might have of these fraction symbols. In the share interpretation of fractions, unit fractions and improper fractions are not accorded a special place.

Also converting an improper fraction to a mixed fraction becomes automatic. 6/5 is the share that one child gets when 6 rotis are shared equally among 5 children and one does this by first distributing one roti to each child and then sharing the remaining 1 roti equally among 5 children giving us the relation

Share interpretation does not provide a direct method to answer the question ‘how much is the given unknown quantity’. To say that the given unknown quantity is 3⁄4 of the whole, one has figure out that four copies of the given quantity put together would make three wholes and hence is equal to one share when these three wholes are shared equally among 4. Share interpretation is also the quotient interpretation of fractions in the sense that 3⁄4 = 3 ÷ 4 and this is important for developing students’ ability to solve problems involving multiplicative and linear functional relations.

To understand the equal share model better, use the GeoGebra file explaining the equal share model available on [[1]]. See figure below. Move the sliders m and n and see how the equal share model is interpreted.

Measure Model

Measure interpretation defines the unit fraction 1/n as the measure of one part when one whole is divided into n equal parts. The composite fraction m/n is as the measure of m such parts. Thus 5/6 is made of 5 piece units of size 1/5 each and 6/5 is made of 6 piece units of size 1/5 each. Since 5 piece units of size make a whole, we get the relation 6/5 = 1 + 1/5.

Significance of measure interpretation lies in the fact that it gives a direct approach to answer the ‘how much’ question and the real task therefore is to figure out the appropriate n so that finitely many pieces of size will be equal to a given quantity. In a sense then, the measure interpretation already pushes one to think in terms of infinitesimal quantities. Measure interpretation is different from the part whole interpretation in the sense that for measure interpretation we fix a certain unit of measurement which is the whole and the unit fractions are sub-units of this whole. The unit of measurement could be, in principle, external to the object being measured.

Introducing Fractions Using Share and Measure Interpretations

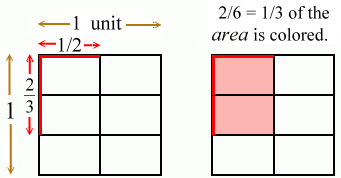
One of the major difficulties a child faces with fractions is making sense of the symbol m/n. In order to facilitate students’ understanding of fractions, we need to use certain models. Typically we use the area model in both the measure and share interpretation and use a circle or a rectangle that can be partitioned into smaller pieces of equal size. Circular objects like roti that children eat every day have a more or less fixed size. Also since we divide the circle along the radius to make pieces, there is no scope for confusing a part with the whole. Therefore it is possible to avoid explicit mention of the whole when we use a circular model. Also, there is no need to address the issue that no matter how we divide the whole into n equal parts the parts will be equal. However, at least in the beginning we need to instruct children how to divide a circle into three or five equal parts and if we use the circular model for measure interpretation, we would need ready made teaching aids such as the circular fraction kit for repeated use.

Rectangular objects (like cake) do not come in the same size and can be divided into n equal parts in more than one way. Therefore we need to address the issues (i) that the size of the whole should be fixed (ii) that all 1⁄2’s are equal– something that children do not see readily. The advantage of rectangular objects is that we could use paper models and fold or cut them into equal parts in different ways and hence it easy to demonstrate for example that 3/5 = 6/10 using the measure interpretation .

Though we expose children to the use of both circles and rectangles, from our experience we feel circular objects are more useful when use the share interpretation as children can draw as many small circles as they need and since the emphasis not so much on the size as in the share, it does not matter if the drawings are not exact. Similarly rectangular objects would be more suited for measure interpretation for, in some sense one has in mind activities such as measuring the length or area for which a student has to make repeated use of the unit scale or its subunits.

Activities

Activity1: Introduction to fractions

Learning Objectives

Introduce fractions using the part-whole method

Materials and resources required

1. Write the Number Name and the number of the picture like the example Number Name = One third Number: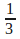

Question: What is the value of the numerator and denominator in the last figure , the answer is

1. Colour the correct amount that represents the fractions

7/10 3/8 1/5 4/7

Question: Before colouring count the number of parts in each figure. What does it represent. Answer: Denominator

1. Divide the circle into fractions and colour the right amount to show the fraction

3/5 6/7 1/3 5/8 2/5

1. Draw the Fraction and observe which is the greater fraction – observe that the parts are equal for each pair

1/3 2/3 4/5 2/5 3/7 4/7

1. Draw the Fraction and observe which is the greater fraction – Observe that the parts are different sizes for each pair.

1/3 1/4 1/5 1/8 1/6 1/2

1. Solve these word problems by drawing
   1. Amar divided an apple into 8 equal pieces. He ate 5 pieces. He put the a other 3 in a box. What fraction did Amar eat?
   2. There are ten biscuits in the box. 3 are cream biscuits. 2 are salt biscuits. 4 are chocolate biscuits. 1 is a sugar biscuit. What fraction of the biscuits in the box are salt biscuits.
   3. Radha has 6 pencils. She gives one to Anil and he gives one to Anita. She keeps the rest. What fraction of her pencils did she give away?
3. The circles in the box represent the whole; colour the right amount to show the fraction Hint: Half is 2 circles

Pre-requisites/ Instructions Method

Do the six different sections given in the activity sheet. For each section there is a discussion point or question for a teacher to ask children.

After the activity sheet is completed, please use the evaluation questions to see if the child has understood the concept of fractions

Evaluation

Activity 2: Proper and Improper Fractions

Learning Objectives

Proper and Improper Fractions

Materials and resources required

1. If you want to understand proper fraction , example 5/6. In the equal share model , 5/6 represents the share that each child gets when 5 rotis are divided among 6 children equally.

1. If you want to understand improper fraction , example 8/3. In the equal share model , 8/3 represents the share that each child gets when 8 rotis are divided among 3 children equally. The child in this case will usually distribute 2 full rotis to each child and then try to divide the remaining rotis. At this point you can show the mixed fraction representation as 2 2/3

Pre-requisites/ Instructions Method

Examples of Proper and improper fractions are given. The round disks in the figure represent rotis and the children figures represent children. Cut each roti and each child figure and make the children fold, tear and equally divide the roits so that each child figure gets equal share of roti.

Evaluation

1. What happens when the numerator and denominator are the same, why ?
2. What happens when the numerator is greater than the denominator why ? How can we represent this in two ways ?

Activity 3: Comparing Fractions

Learning Objectives

Comparing-Fractions

Materials and resources required

[[2]]

[[3]]

Pre-requisites/ Instructions Method

Print the document and work out the activity sheet

Evaluation

1. Does the child know the symbols >, < and =
2. What happens to the size of the part when the denominator is different ?
3. Does it decrease or increase when the denominator becomes larger ?
4. Can we compare quantities when the parts are different sizes ?
5. What should we do to make the sizes of the parts the same ?

Activity 4: Equivalent Fractions

Learning Objectives

To understand Equivalent Fractions

Materials and resources required

[[4]]

Pre-requisites/ Instructions Method

Print 10 copies of the document from pages 2 to 5 fractions-matching-game Cut the each fraction part. Play memory game as described in the document in groups of 4 children.

Evaluation

1. What is reducing a fraction to the simplest form ?
2. What is GCF – Greatest Common Factor ?
3. Use the document simplifying-fractions.pdf
4. Why are fractions called equivalent and not equal.

Errors with fractions

Introduction

A brief understanding of the common errors that children make when it comes to fractions are addressed to enable teachers to understand the child's levels of conceptual understanding to address the misconceptions.

Objectives

When fractions are operated erroneously like natural numbers, i.e. treating the numerator and the denominators separately and not considering the relationship between the numerator and the denominator is termed as N-Distractor. For example 1/3 + ¼ are added to result in 2/7. Here 2 units of the numerator are added and 3 & four units of the denominator are added. This completely ignores the relationship between the numerator and denominator of each of the fractions. Streefland (1993) noted this challenge as N-distractors and a slow-down of learning when moving from the concrete level to the abstract level.

N-Distractors

The five levels of resistance to N-Distractors that a child develops are:

1. Absence of cognitive conflict: The child is unable to recognize the error even when she sees the same operation performed resulting in a correct answer. The child thinks both the answers are the same in spite of different results. Eg. ½ + ½ she erroneously calculated as 2/4. But when the child by some other method, say, through manipulatives (concrete) sees ½ + ½ = 1 does not recognize the conflict.
2. Cognitive conflict takes place: The student sees a conflict when she encounters the situation described in level 1 and rejects the ½+1/2 = 2/4 solution and recognizes it as incorrect. She might still not have a method to arrive at the correct solution.
3. Spontaneous refutation of N-Distractor errors: The student may still make N-Distractor errors, but is able to detect the error for herself. This detection of the error may be followed by just rejection or explaining the rejection or even by a correct solution.
4. Free of N-Distractor: The written work is free of N-Distractors. This could mean a thorough understanding of the methods/algorithms of manipulating fractions.
5. Resistance to N-Distractor: The student is completely free (conceptually and algorithmically) of N-Distractor errors.

Further Exploration

1. www.merga.net.au/publications/counter.php?pub=pub_conf&id=1410 A PDF Research paper titled Probing Whole Number Dominance with Fractions.
2. www.merga.net.au/documents/RP512004.pdf A PDF research paper titled “Why You Have to Probe to Discover What Year 8 Students Really Think About Fractions ”
3. [[5]] A google book Fractions in realistic mathematics education: a paradigm of developmental ...By Leen Streefland

Operations on Fractions

Introduction

This topic introduces the different operations on fractions. When learners move from whole numbers to fractions, many of the operations are counter intuitive. This section aims to clarify the concepts behind each of the operations.

Objectives

The aim of this section is to visualise and conceptually understand each of the operations on fractions.

Addition and Subtraction

Adding and subtracting like fractions is simple. It must be emphasised thought even during this process that the parts are equal in size or quantity because the denominator is the same and hence for the result we keep the common denominator and add the numerators.

Adding and subtracting unlike fractions requires the child to visually understand that the parts of each of the fractions are differing in size and therefore we need to find a way of dividing the whole into equal parts so that the parts of all of the fractions look equal. Once this concept is established, the terms LCM and the methods of determining them may be introduced.

Multiplication

Multiplying a fraction by a whole number: Here the repeated addition logic of multiplying whole numbers is still valid. 1/6 multiplied by 4 is 4 times 1/6 which is equal to 4/6.

Multiplying a fraction by a fraction: In this case the child is confused as repeated addition does not make sense. To make a child understand the of operator we can use the language and demonstrate it using the measure model and the area of a rectangle.

The area of a rectangle is found by multiplying side length by side length. For example, in the rectangle below, the sides are 3 units and 9 units, and the area is 27 square units.

We can apply that idea to fractions, too.

• The one side of the rectangle is 1 unit (in terms of length).
• The other side is 1 unit also.
• The whole rectangle also is 1 square unit, in terms of area.

See figure below to see how the following multiplication can be shown.

Remember: The two fractions to multiply represent the length of the sides, and the answer fraction represents area.

Division

Dividing a fraction by a whole number can be demonstrated just like division of whole numbers. When we divide 3/4 by 2 we can visualise it as dividing 3 parts of a whole roti among 4 people.

Here 3/4 is divided between two people. One fourth piece is split into two. Each person gets 1/4 and 1/8.

OR

Another way of solving the same problem is to split each fourth piece into 2.

This means we change the 3/4 into 6/8.

When dividing a fraction by a fraction, we use the measure interpretation.

When we divide 2 by ¼ we ask how many times does ¼

fit into 2.

It fits in 4 times in each roti, so totally 8 times.

We write it as

Activities

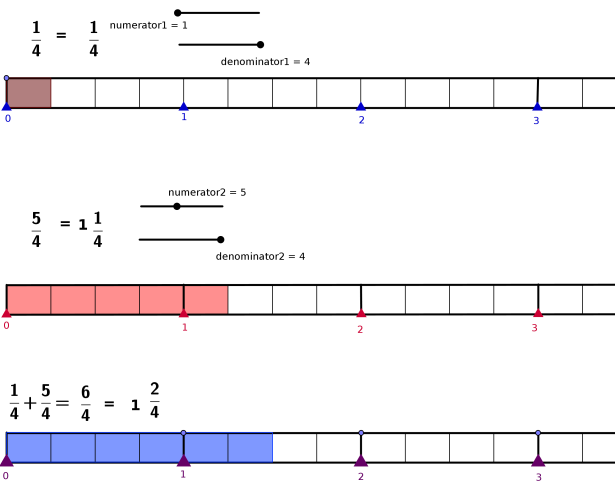
Activity 1 Addition of Fractions

Learning Objectives

Understand Addition of Fractions

Materials and resources required

[[6]]

Pre-requisites/ Instructions Method

Open link [[7]]

Move the sliders Numerator1 and Denominator1 to set Fraction 1

Move the sliders Numerator2 and Denominator2 to set Fraction 2

See the last bar to see the result of adding fraction 1 and fraction 2

When you move the sliders ask children to

Observe and describe what happens when the denominator is changed.

Observe and describe what happens when denominator changes

Observe and describe the values of the numerator and denominator and relate it to the third result fraction.

Discuss LCM and GCF

Evaluation

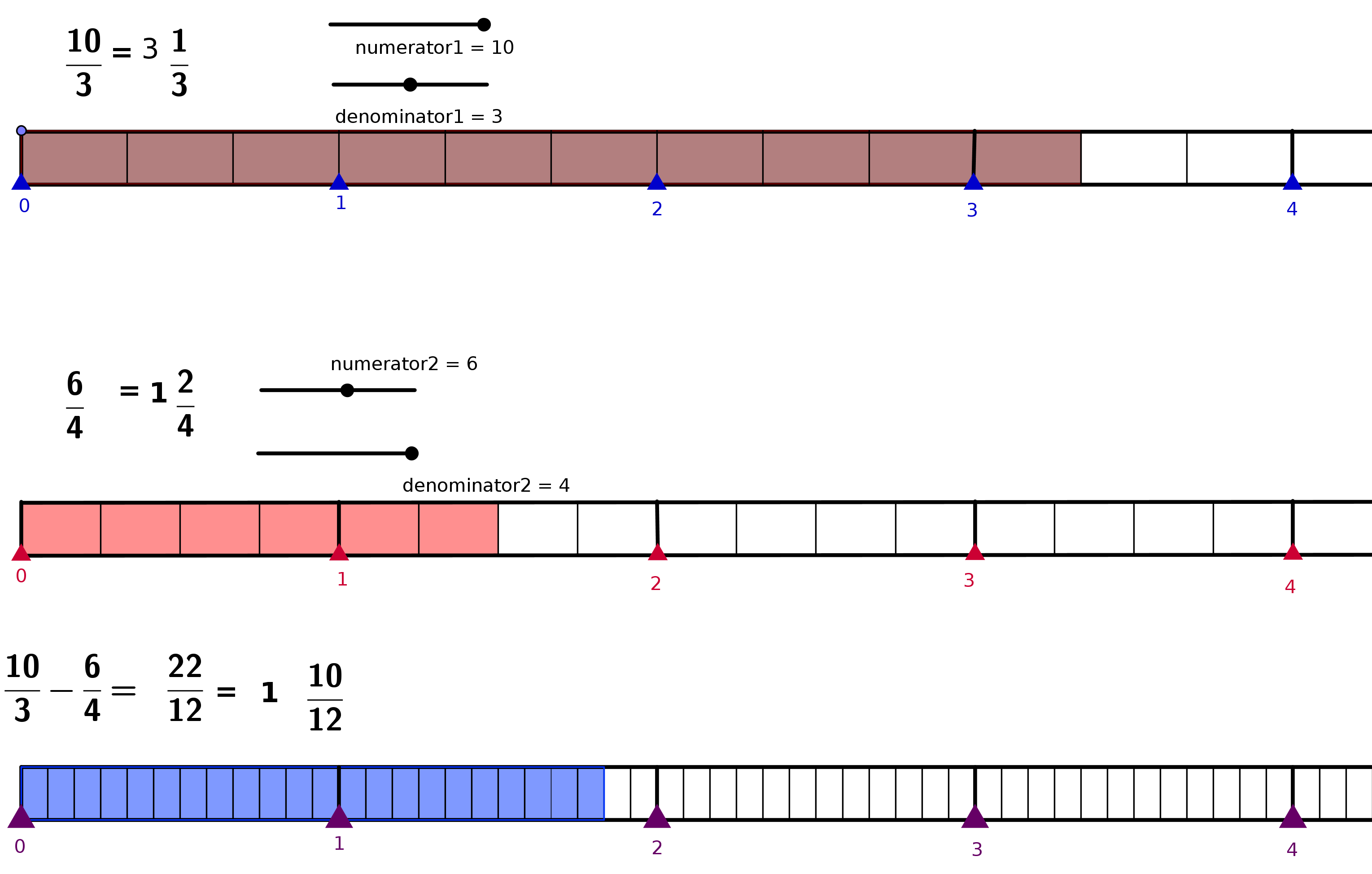
Activity 2 Fraction Subtraction

Learning Objectives

Understand Fraction Subtraction

Materials and resources required

[[8]]

Pre-requisites/ Instructions Method

Open link [[9]]

Move the sliders Numerator1 and Denominator1 to set Fraction 1

Move the sliders Numerator2 and Denominator2 to set Fraction 2

See the last bar to see the result of subtracting fraction 1 and fraction 2

When you move the sliders ask children to

observe and describe what happens when the denominator is changed.

observe and describe what happens when denominator changes

observe and describe the values of the numerator and denominator and relate it to the third result fraction.

Discuss LCM and GCF

Evaluation

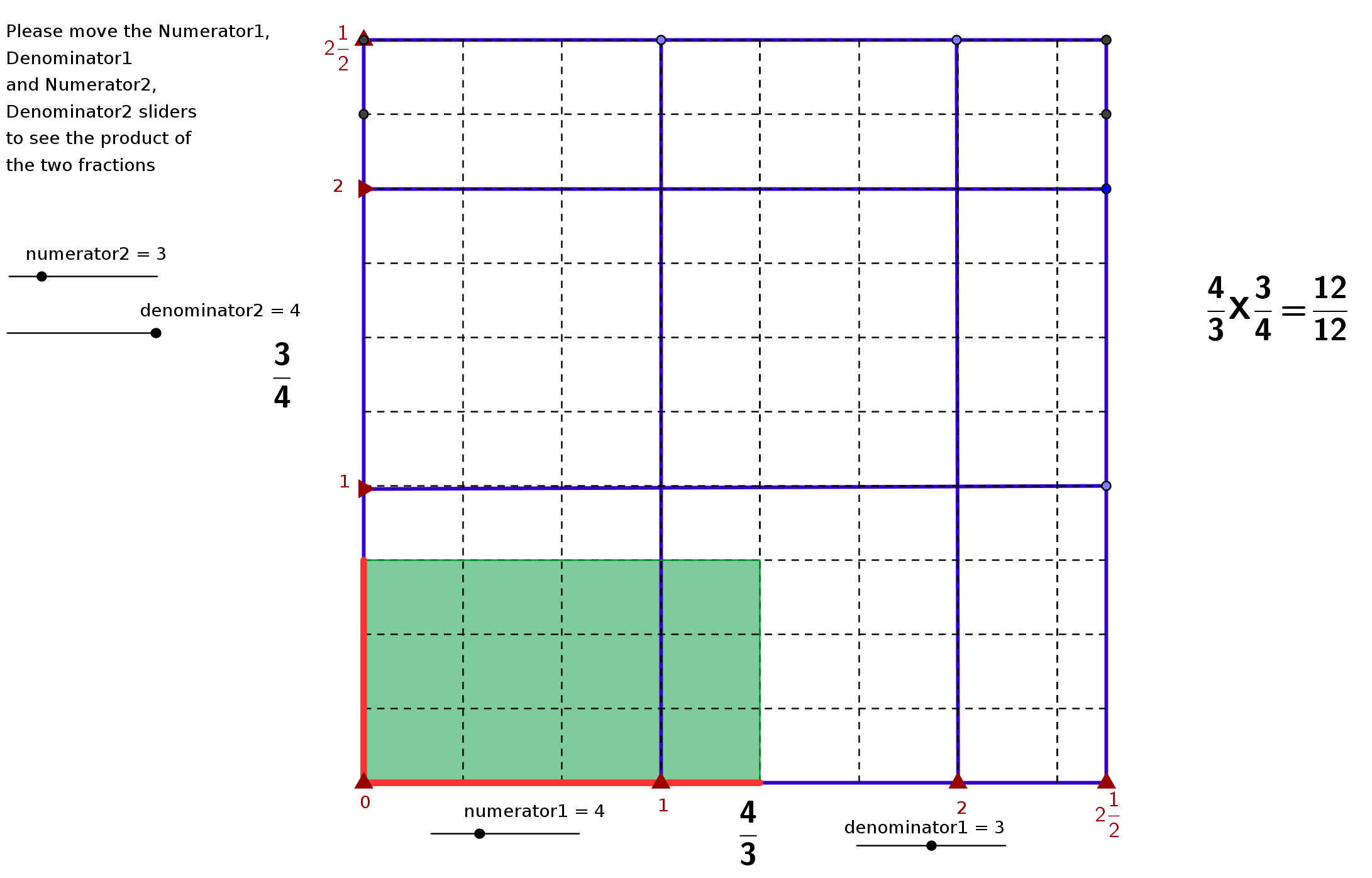
Activity 3 Multiplication of fractions

Learning Objectives

Understand Multiplication of fractions

Materials and resources required

[[10]]

Pre-requisites/ Instructions Method

Open link [[11]]

Move the sliders Numerator1 and Denominator1 to set Fraction 1

Move the sliders Numerator2 and Denominator2 to set Fraction 2

On the right hand side see the result of multiplying fraction 1 and fraction 2

Material/Activity Sheet

Please open [[12]] in Firefox and follow the process

When you move the sliders ask children to

observe and describe what happens when the denominator is changed.

observe and describe what happens when denominator changes

One unit will be the large square border-in blue solid lines

A sub-unit is in dashed lines within one square unit.

The thick red lines represent the fraction 1 and 2 and also the side of the quadrilateral

The product represents the area of the the quadrilateral

Evaluation

When two fractions are multiplied is the product larger or smaller that the multiplicands – why ?

Activity 4 Division by Fractions

Learning Objectives

Understand Division by Fractions

Materials and resources required

[[13]]

Crayons/ colour pencils, Scissors, glue

Pre-requisites/ Instructions Method

Print out the pdf [[14]]

Colour each of the unit fractions in different colours. Keep the whole unit (1) white.

Cut out each unit fraction piece.

Give examples

For example if we try the first one, See how many strips will fit exactly onto whole unit strip.

Evaluation

When we divide by a fraction is the result larger or smaller why ?

Further Exploration

1. [[15]] detailed conceptual understanding of division by fractions
2. [[16]] understanding fractions
3. [[17]] Worksheets in mathematics for teachers to use

Linking Fractions to other Topics

Introduction

It is also very common for the school system to treat themes in a separate manner. Fractions are taught as stand alone chapters. In this resource book an attempt to connect it to other middle school topics such as Ratio Proportion, Percentage and high school topics such as rational and irrational numbers, inverse proportions are made. These other topics are not discussed in detail themselves, but used to show how to link these other topics with the already understood concepts of fractions.

Objectives

Explicitly link the other topics in school mathematics that use fractions.

Decimal Numbers

“Decimal” comes from the Latin root decem, which simply means ten. The number system we use is called the decimal number system, because the place value units go in tens: you have ones, tens, hundreds, thousands, and so on, each unit being 10 times the previous one.

In common language, the word “decimal number” has come to mean numbers which have digits after the decimal point, such as 5.8 or 9.302. But in reality, any number within the decimal number system could be termed a decimal number, including whole numbers such as 12 or 381.

The simplest way to link or connect fractions to the decimal number system is with the number line representation. Any scale that a child uses is also very good for this purpose, as seen in the figure below.

The number line between 0 and 1 is divided into ten parts. Each of these ten parts is 1/10, a tenth.

Under the tick marks you see decimal numbers such as 0.1, 0.2, 0.3, and so on. These are the same numbers as the fractions 1/10, 2/10, 3/10 and so on.

We can write any fraction with tenths (denominator 10) using the decimal point. Simply write after the decimal point how many tenths the number has. 0.6 means six tenths or 1/6. 1.5 means 1 whole and 5 tenths or

Note: A common error one sees is 0.7 is written as 1 /7. It is seven tenths and not one seventh. That the denominator is always 10 has to be stressed. To reinforce this one can use a simple rectangle divided into 10 parts , the same that was used to understand place value in whole numbers.

The coloured portion represents 0.6 or 6/10 and the whole block represents 1.

Percentages

Fractions and percentages are different ways of writing the same thing. When we say that a book costs Rs. 200 and the shopkeeper is giving a 10 % discount. Then we can represent the 10% as a fraction as where 10 is the numerator and the denominator is always 100. In this case 10 % of the cost of the book is . So you can buy the book for 200 – 20 = 180 rupees.

There are a number of common ones that are useful to learn. Here is a table showing you the ones that you should learn.

Percentage	Fraction
100%
50%
25%
75%
10%
20%
40%

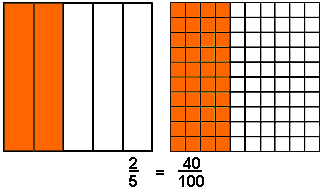To see 40 % visually see the figure :

You can see that if the shape is divided into 5 equal parts, then 2 of those parts are shaded.

If the shape is divided into 100 equal parts, then 40 parts are shaded.

These are equivalent fractions as in both cases the same amount has been shaded.

Ratio and Proportion

It is important to understand that fractions also can be interpreted as ratio's. Stressing that a fraction can be interpreted in many ways is of vital importance. Here briefly I describe the linkages that must be established between Ratio and Proportion and the fraction representation. Connecting multiplication of fractions is key to understanding ratio and proportion.

What is ratio?

Ratio is a way of comparing amounts of something. It shows how much bigger one thing is than another. For example:

• Use 1 measure detergent (soap) to 10 measures water
• Use 1 shovel (bucket) of cement to 3 shovels (buckets) of sand
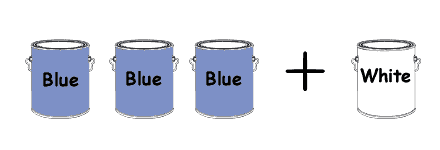
• Use 3 parts blue paint to 1 part white

Ratio is the number of parts to a mix. The paint mix is 4 parts, with 3 parts blue and 1 part white.

The order in which a ratio is stated is important. For example, the ratio of soap to water is 1:10. This means for every 1 measure of soap there are 10 measures of water.

Mixing paint in the ratio 3:1 (3 parts blue paint to 1 part white paint) means 3 + 1 = 4 parts in all.

3 parts blue paint to 1 part white paint = is ¾ blue paint to ¼ white paint.

Cost of a pen is Rs 10 and cost of a pencil is Rs 2. How many times the cost of a pencil is the cost of a pen? Obviously it is five times. This can be written as

The ratio of the cost of a pen to the cost of a pencil =

What is Direct Proportion ?

Two quantities are in direct proportion when they increase or decrease in the same ratio. For example you could increase something by doubling it or decrease it by halving. If we look at the example of mixing paint the ratio is 3 pots blue to 1 pot white, or 3:1.

Paint pots in a ratio of 3:1

But this amount of paint will only decorate two walls of a room. What if you wanted to decorate the whole room, four walls? You have to double the amount of paint and increase it in the same ratio.

If we double the amount of blue paint we need 6 pots.

If we double the amount of white paint we need 2 pots.

Six paint pots in a ratio of 3:1

The amount of blue and white paint we need increase in direct proportion to each other. Look at the table to see how as you use more blue paint you need more white paint:

Pots of blue paint 3 6 9 12

Pots of white paint 1 2 3 4

Two quantities which are in direct proportion will always produce a graph where all the points can be joined to form a straight line.

What is Inverse Proportion ?

Two quantities may change in such a manner that if one quantity increases the the quantity decreases and vice-versa. For example if we are building a room, the time taken to finish decreases as the number of workers increase. Similarly when the speed increases the time to cover a distance decreases. Zaheeda can go to school in 4 different ways. She can walk, run, cycle or go by bus.

Study the table below, observe that as the speed increases time taken to cover the distance decreases

	Walk	Run	Cycle	Bus
Speed Km/Hr	3	6 (walk speed *2)	9 (walk speed *3)	45 (walk speed *15)
Time Taken (minutes)	30	15 (walk Time * ½)	10 (walk Time * 1/3)	2 (walk Time * 1/15)

As Zaheeda doubles her speed by running, time reduces to half. As she increases her speed to three times by cycling, time decreases to one third. Similarly, as she increases her speed to 15 times, time decreases to one fifteenth. (Or, in other words the ratio by which time decreases is inverse of the ratio by which the corresponding speed increases). We can say that speed and time change inversely in proportion.

Moving from Additive Thinking to Multiplicative Thinking

Avinash thinks that if you use 5 spoons of sugar to make 6 cups of tea, then you would need 7 spoons of sugar to make 8 cups of tea just as sweet as the cups before. Avinash would be using an additive transformation'''; he thinks that since we added 2 more cups of tea from 6 to 8. To keep it just as sweet he would need to add to more spoons of sugar. What he does not know is that for it to taste just as sweet he would need to preserve the ratio of sugar to tea cup and use multiplicative thinking. He is unable to detect the ratio.

Proportional Reasoning

Proportional thinking involves the ability to understand and compare ratios, and to predict and produce equivalent ratios. It requires comparisons between quantities and also the relationships between quantities. It involves quantitative thinking as well as qualitative thinking. A feature of proportional thinking is the multiplicative relationship among the quantities and being able to recognize this relationship. The relationship may be direct (divide), i.e. when one quantity increases, the other also increases. The relationship is inverse (multiply), when an increase in one quantity implies a decrease in the other, in both cases the ratio or the rate of change remains a constant.

The process of adding involved situations such as adding, joining, subtracting, removing actions which involves the just the two quantities that are being joined, while proportional thinking is associated with shrinking, enlarging, scaling , fair sharing etc. The process involves multiplication. To be able to recognize, analyse and reason these concepts is multiplicative thinking/reasoning. Here the student must be able to understand the third quantity which is the ratio of the two quantities. The preservation of the ratio is important in the multiplicative transformation.

Rational & Irrational Numbers

After the number line was populated with natural numbers, zero and the negative integers, we discovered that it was full of gaps. We discovered that there were numbers in between the whole numbers - fractions we called them.

But, soon we discovered numbers that could not be expressed as a fraction. These numbers could not be represented as a simple fraction. These were called irrational numbers. The ones that can be represented by a simple fraction are called rational numbers. They h ad a very definite place in the number line but all that could be said was that square root of 2 is between 1.414 and 1.415. These numbers were very common. If you constructed a square, the diagonal was an irrational number. The idea of an irrational number caused a lot of agony to the Greeks. Legend has it that Pythagoras was deeply troubled by this discovery made by a fellow scholar and had him killed because this discovery went against the Greek idea that numbers were perfect.

How can we be sure that an irrational number cannot be expressed as a fraction? This can be proven algebraic manipulation. Once these "irrational numbers" came to be identified, the numbers that can be expressed of the form p/q where defined as rational numbers.

There is another subset called transcendental numbers which have now been discovered. These numbers cannot be expressed as the solution of an algebraic polynomial. "pi" and "e" are such numbers.

Activities

Activity 1 Fractions representation of decimal numbers

Learning Objectives

Fractions representation of decimal numbers

Materials and resources required

[[18]]

[[19]]

Pre-requisites/ Instructions Method

Make copies of the worksheets

[[20]]

[[21]]

Evaluation

1. Draw a number line and name the fraction and decimal numbers on the number line. Take a print of the document [[22]] . Ask students to place any fraction and decimal numbers between between 0 and 10 on the number line
2. Write 0.45, 0.68, 0.05 in fraction form and represent as a fraction 100 square.

Activity 2 Fraction representation and percentages

Learning Objectives

Understand fraction representation and percentages

Materials and resources required

[[23]]

[[24]]

Pre-requisites/ Instructions Method

Please print copies of the 2 activity sheets [[25]] and [[26]] and discuss the various percentage quantities with the various shapes.

Then print a copy each of spider-percentages.pdf and make the children do this activity

Evaluation

1. What value is the denominator when we represent percentage as fraction ?
2. What does the numerator represent ?
3. What does the whole fraction represent ?
4. What other way can we represent a fraction whose denominator is 100.

Activity 3 Fraction representation and rational and irrational numbers

Learning Objectives

Understand fraction representation and rational and irrational numbers

Materials and resources required

Thread of a certain length.

Pre-requisites/ Instructions Method

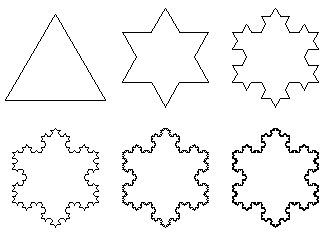
Construct Koch's snowflakes .

Start with a thread of a certain length (perimeter) and using the same thread construct the following shapes (see Figure).

See how the shapes can continue to emerge but cannot be identified definitely with the same perimeter (length of the thread).

Identify the various places where pi, "e" and the golden ratio occur

Evaluation

1. How many numbers can I represent on a number line between 1 and 2.
2. What is the difference between a rational and irrational number, give an example ?
3. What is Pi ? Why is it a special number ?

Further Exploration

1. Percentage and Fractions, [[27]]
2. A mathematical curve Koch snowflake, [[28]]
3. Bringing it Down to Earth: A Fractal Approach, [[29]]

See Also

1. Video on teaching fractions using the equal share method made by Eklavya an NGO based in Madhya Pradesh, India [[30]]
2. Mathematics resources from Homi Baba Centre for Science Education , [[31]]
3. [[32]] Understand how to use Geogebra a mathematical computer aided tool

Books

1. [[33]] A google book Fractions in realistic mathematics education: a paradigm of developmental ...By Leen Streefland

References

1. Introducing Fractions Using Share and Measure Interpretations: A Report from Classroom Trials . Jayasree Subramanian, Eklavya, Hoshangabad, India and Brijesh Verma,Muskan, Bhopal, India
2. Streefland, L. (1993). “Fractions: A Realistic Approach.” In Carpenter, T.P., Fennema, E., Romberg, T.A. (Eds.), Rational Numbers: an Integration of Research. (289-325). New Jersey: Lawrence, Erlbaum Associates, Publishers.