A Trapezium and its properties
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Error: Mind Map file trapezium.mm not found
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Useful websites
Reference Books
Teaching Outlines
Concept # A Trapezium and its properties
Learning objectives
- A quadrangle with only two opposite sides parallel is called a trapezium, or trapezoid.
- The parallel sides are called the bases of the trapezium and the other two sides are called the legs or the lateral sides.
- If the legs are equal in length, then this is an isosceles trapezium.
- The distance between the bases is called height of trapezium.
Notes for teachers
Activity No # 1. Properties of a trapezium.
- Estimated Time :40 minutes.
- Materials/ Resources needed:
Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any
- The students should have prior knowledge about parallel lines, angles and diagnols.
- Multimedia resources: Laptop.
- Website interactives/ links/ / Geogebra Applets
- Process:
- The teacher can introduce the shape of the trapezium and can explain its properties with the help of this geogebra file.
- Developmental Questions:
- What is a trapezium ?
- How many sides does it have ?
- What can be said about the pair of sides ?
- Identify the diagnols. Are they equal ?
- What would be the sum of 4 angles of the trapezium ? Why so ?
- What would be the sum of its two allied angles ?
- Are the two pairs of sides of a trapezium equal ?
- Evaluation:
Are the students able to apply the theorems of parallel lines - transversal to prove the properties.
- Why are allied angles of the trapezium supplementary ?
- Are the diagnols equal ?
- Is trapezium a parallelogram ?
- Question Corner:
- List the properties of a trapezium.
- What properties of other quadrilaterals does it share. Compare with other quadrilaterals.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept #2. Measurements in Trapezium
Learning objectives
- The trapeium contains two parallel sides and two non-parallel sides.
- The area of trapezium is found by viewing it as a parallelogram.
- The area of trapezium is 1/2(a+b)h where a and b are its parallel sides and h is the perpendicular distance between them.
- The perimeter of a trapezium is obtained by sum of its 4 sides.
Notes for teachers
- The area of most figures can be expressed in terms of its dimensions.
- The area of most composite figures can be calculated using the area of primary figures.
Activity No # 1.Area of a trapezium
- Estimated Time: 20 minutes.
- Materials/ Resources needed : Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any
- The students should know a parallelogram and formula to find its area.
- They should know the trapezium and its properties.
- Multimedia resources: Laptop
- Website interactives/ links/ / Geogebra Applets
- Process:
- The teacher can initially discuss about a trapezium.
- She can then reiterate that formula for area of certain composite figures can be found by converting them into known simple figures.
- Here the trapezium is converted into a parallelogram.
- Area of parallelogram is then deduced.
- Developmental Questions:
- What is a trapezium ?
- Name its two parallel sides.
- What is meant by the height of the trapezium ?
- After cutting the trapezium exactly in the centre what would be the new height ?
- What is the length of the new parallelogram formed ?
- What is the formula to find the area of a parallelogram ?
- What is the area of this parallelogram formed from a trapezium ?
- Evaluation:
- Explain the sequence of steps involved in deriving the formula for the area of a trapeium.
- Question Corner:
- Recall the steps involved in deriving the formula for area of a parallelogram.
Concept # 3.Construction of Trapezium
Learning objectives
- The students should be able to construct a trapezium accurately for the given measurements.
Notes for teachers
Activity No #
- Estimated Time: 40 minutes.
- Materials/ Resources needed: a ruler, pencil, compass, and a blank piece of paper
- Prerequisites/Instructions, if any
- The students should know to use a compass and draw perpendicular lines.
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
This has been taken from the website ; http://www.k6-geometric-shapes.com/trapezoid.html
- Process:
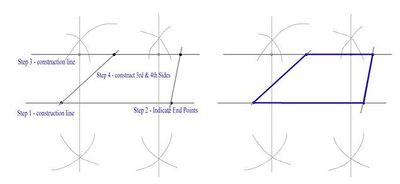
- This construction can be made if the height of the trapezium along with the length of the four sides is known.
- Draw a straight line lightly using your ruler and pencil on your paper. - This is what is called a construction line, and will be the base of the trapezium.
- Indicate the two end points of the base of the shape with two points, measured by ruler.
Note:We know that the top and base line of a trapezium are parallel, and, we know the distance between them (the height).
- Using compass, construct two lines (lightly) perpendicular to the base. On both of these lines measure the height of the trapezium, and indicate with two points (one on each perpendicular) Connect these two points using a light construction line. The second side of the trapezium will be 'somewhere' on this line.
- Using ruler, measure the length of the third and fourth sides between these two paralell lines, using the points on the first construction line, as one end of the line segment. Mark with a point.
Note: You will now have four construction lines, intersecting at four vertices.
- The required trapezium is the shape contained between the four points of intersection of these four lines.
- Using a heavier line connect the four points to finish your shape.
- Developmental Questions:
- Name the given parameters of a trapezium.
- What would be the base ?
- What are the measures of its 2 parallel sides ?
- What is the measure of its height ?
- How would you start the construction process ?
- what is the method to draw perpendicular lines ?
- How do you mark the height of the trapezium ?
- Evaluation:
The teacher can check the students constructions to evaluate.
- Question Corner:
- Can you construct a trapezium when only its area is known ? Discuss.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept # 4. Isosceles trapezium
Learning objectives
- A trapezium in which non-parallel sides and base angles are equal is called as an Isosceles Trapezium.
- The diagonals of an isosceles trapezium are equal.
- Area of isosceles trapezoid is given by , where a and b are the lengths of the parallel sides and h is the distance (height) between the parallel sides.
Notes for teachers
Activity No # Construct an isosceles trapezium and study its properties
- Estimated Time: 40 minutes.
- Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any
- The students should know the concepts of parallel lines, perpendicular lines and rectangle.
- They should know basic constructions like parallel lines and perpendicular lines.
- Multimedia resources: Laptop.
- Website interactives/ links/ / Geogebra Applets
- Process:
- Construct AB.
- Construct the midpoint C of AB.
- Construct a line through point C perpendicular to AB.
- Construct AD.
- Mark the perpendicular line as a mirror, then reflect AD and point D.
- Construct DD'.
- Hide the perpendicular line and midpoint C.
- Drag points A, B, and D to make trapezoids of different sizes and shapes. Make sure you note when your trapezoid turns into a rectangle.
- Based on your construction, describe the symmetry of an isosceles trapezoid.
- Measure the four angles in your trapezoid. 10. Drag the vertices of the trapezoid and observe your angle measures.
- Make a conjecture about the base angles of an isosceles trapezoid. (Both of the parallel sides are considered bases, so a trapezoid has two pairs of base angles.)
- Developmental Questions
- Evaluation
- Question Corner
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Hints for difficult problems
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template