Graphs and polyhedra problems

Problem 1

Statement : The Königsberg bridge problem : if the seven bridges of the city of Königsberg (left figure; Kraitchik 1942), formerly in Germany but now known as Kaliningrad and part of Russia, over the river Preger can all be traversed in a single trip without doubling back, with the additional requirement that the trip ends in the same place it began.

Image Courtesy : http://mathworld.wolfram.com/KoenigsbergBridgeProblem.html

Interpretation :

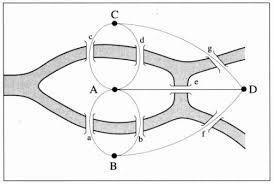
This is equivalent to asking if the multigraph on four nodes and seven edges (right figure) has an Eulerian cycle. This problem was answered in the negative by Euler (1736), and represented the beginning of graph theory.
For Konigsberg, let us represent land with red dots and bridges with black curves, or arcs:

Thus, in its stripped down version, the seven bridges problem looks like this:

The problem now becomes one of drawing this picture without retracing any line and without picking your pencil up off the paper. Consider this: all four of the vertices in the above picture have an odd number of arcs connected to them. Take one of these vertices, say one of the ones with three arcs connected to it. Say you're going along, trying to trace the above figure out without picking up your pencil.
The first time you get to this vertex, you can leave by another arc. But the next time you arrive, you can't. So you'd better be through drawing the figure when you get there! Alternatively, you could start at that vertex, and then arrive and leave later. But then you can't come back. Thus every vertex with an odd number of arcs attached to it has to be either the beginning or the end of your pencil-path. So you can only have up to two 'odd' vertices! Thus it is impossible to draw the above picture in one pencil stroke without retracing.