Science/Motion
Introduction
- Motion in one dimension
In this unit, we will attempt to understand and describe motion and explain the motion of objects. Kinematics is the science of describing the motion of objects using
words, diagrams, numbers, graphs, and equations.
We have already seen that the study of Physics is about building models and a framework to explain the phenomena we observe. If we need to build a model, we need to develop a common vocabulary to describe our observations. Once we have the vocabulary, we can use that to analyze the motion of objects and ultimately explain how they move in the way they do.
In this unit, we will study Motion in One Dimension and the equations of motion that describe the case of motion with uniform acceleration.
Concept Map
This concept map needs some work. Please refine it and share on the mathssciencestf@googlegroups.com.
Distance and displacement
In the world around us, we see different objects around us. What would be one of the first observations you would make about an object? The first thing we
would notice (other than the shape, size, color, etc.) is whether it is moving or at rest. We often perceive motion (movement) when
something changes its position with respect to time. Alternatively, we can infer that something has moved after observing its
surroundings. Can you think of examples that describe both these?
When we begin to describe motion, the first thing that comes to mind is that of direction. It is not enough to know that something has moved; it is equally important to know where it has moved. There are many quantities in Physics that get their relevance from the direction in which they are operating.
When a quantity can be described just by its magnitude, it is called a scalar. For instance, mass. It is not very meaningful to say, that body A has mass 20 kg in the eastern direction. On the other hand, I do need to know which is the path to take from Town A to Town B. The description of the path from A to B is meaningful when I know the direction of travel.
- Scalars are quantities which are fully described by a magnitude (or numerical value) alone. Mass, volume, area, temperature, etc. are scalars.
- Vectors are quantities which are fully described by both a magnitude and a direction.
- Rest : When a body does not change its position with respect to surroundings, then it is said to be in a state of rest.
- Motion: When a body changes its position with respect to surroundings, then it is said to be in a state of motion.
This notion of rest and motion is very relative. In everyday instances, we have several examples of this relative movement with respect to another. (people inside a bus move with respect to those standing on the ground, trees appearing to move backwards when seen from a train moving forward). The next question that comes is what we are measuring when we describe motion. There are several terms that we need to define to describe motion. These are distance, displacement, speed, velocity, acceleration, uniform, non-uniform, etc.
- Distance: Distance is the length of the path traveled in a certain time.
- Displacement: Displacement is the shortest distance between the initial and final position.
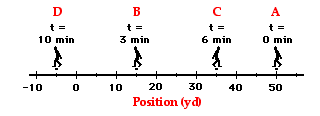
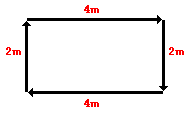The
physics teacher has worked hard and traveled a distance of 12 m but
her effective displacement from the initial position, A, is zero.
Since, we are only interested in
the initial and final positions for displacement, we are interested
in the final position with respect to the initial position – to the
left of, to the right of, in front of, etc.
What
is the effective displacement and the distance traveled starting at
t = 0 minutes?
That brings us to the idea of
direction. A measure of displacement makes sense only when we have
the direction in which the displacement occurs. Also associated with
the idea of displacement is the notion of a reference point, the
initial position with respect to which the displacement occurs.
Motion can occur in a number of
complex ways – straight line, circular, or any combination thereof.
We will discuss in this module straight line and circular motion.
Speed and velocity
Closely associated with the definitions of distance and displacement is that of speed and velocity. Obviously, if an object has covered a certain distance, it has done so over a certain time. This time over which the distance is covered will be different for different objects.
We describe this rate of motion
of objects in terms of its speed.
- Average speed = Total distance traveled/ Total time taken
- If an object travels a certain distance, s, in time t, then the speed, v, is given by v = s/t.
----------------------------------------------------------
An object travels 16 m in 4
seconds and then another 16 m in 2 seconds. What is the average
speed of the object?
Total distance = 32 m
Total time = 6 seconds
Average speed = 32/ 6 = 5.33 m/s
----------------------------------------------------------
We have already seen that
direction is needed to describe any motion meaningfully. The change
in displacement of an object, in time t, can be expressed as its
velocity.
- Velocity is defined as (final position – initial position)/ time taken. Velocity is a vector quantity and needs both magnitude and direction.
- Velocity describes the speed and the direction in which the motion has occurred.
When evaluating the velocity of
an object, one must keep track of direction. It would not be enough
to say that an object has a velocity of 55 mi/hr. One must include
direction information in order to fully describe the velocity of the
object. For instance, you must describe an object's velocity as being
55 mi/hr, east. This is one of the essential differences
between speed and velocity. Speed is a scalar quantity and does not
keep track of direction; velocity is a vector quantity and is
direction aware.
The task of describing the
direction of the velocity vector is easy. The direction of the
velocity vector is simply the same as the direction which an object
is moving. It would not matter whether the object is speeding up or
slowing down. If an object is moving rightwards, then its velocity is
described as being rightwards. If an object is moving downwards, then
its velocity is described as being downwards. So an airplane moving
towards the west with a speed of 300 mi/hr has a velocity of 300
mi/hr, west.
It is important to understand
that an average speed or average velocity does not suggest that the
entire distance was traveled at that speed or that the entire
displacement occurred at that rate. An average only considers the
overall distance (displacement) over a give time interval and
calculates the average speed or velocity.
Since
a moving object often changes its speed during its motion, it is
common to distinguish
between the average speed and the instantaneous speed. The
distinction is as follows.
- Instantaneous Speed - the speed at any given instant in time.
- Average Speed - the average of all instantaneous speeds; found simply by a distance/time ratio.
- Average velocity - the total displacement divided by the time over which the displacement occurs
- Instantaneous velocity - the average velocity calculated for a very small time interval
If an object is moving in a single direction, the speed could be either constant, changing uniformly (constantly) or changing in a non-uniform way. An object’s velocity can change either in terms of magnitude (the rate at which actual physical units of space are covered) or the direction in which the motion has occurred. If the velocity or the speed is changing at a uniform rate, then the average speed or velocity is given by the arithmetic mean.
- Average velocity = (initial velocity + final velocity)/ 2
- Average speed = (initial speed + final speed)/ 2
- The units of speed and velocity are m/s.
----------------------------------------------------------
Check your understanding
- An object has moved through a distance. Can it have zero displacement?
- A farmer moves along the boundary of a square field of side 10m in 40 seconds. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds?
- Which of the following is true for displacement?
- It cannot be zero
- Its magnitude is greater than the distance traveled by the object.
- Usha swims in a 90 m long pool. She covers 180 m in one minite by swimming from one end of the pool to another and back along the same straight path. Find her average speed and velocity.
- Under what conditions is the magnitude of average velocity of an object equal to its average speed?
- What does the odometer of an automobile measure?
----------------------------------------------------------
Rate of change of velocity
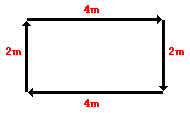Let
us go back to our Physics teacher walking along the boundary. She
may cover 4m East in 2 seconds; 2m South in 2 seconds, 4 m West in 4
seconds and 2 m North in 1 second. Her speed and velocity on each of
these sectors is different.
A moving object may not always move at the same rate not does it always have to move at variable
rates. An object moving at constant velocity is an example of
uniform motion. Velocity varies with time in non-uniform motion.
Most objects have a combination of uniform and non-uniform motion.
Your drive from school to home is an example of non-uniform motion.
Can you think of an object with a uniform motion?
Once we know that an object has a
variable velocity, we need to find out how much does the velocity has
changed. We do this with by measuring the acceleration, defined as:
- Acceleration = Change in velocity / time taken
- If the velocity of an object changes from “u” to “v” in time t, then the acceleration is given by a = (v – u)/ t.
Since acceleration is change in velocity in a given time, its units should be m/s per second, m/s2 .
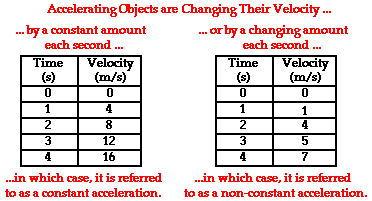
The acceleration can be uniform
or non-uniform. Uniform acceleration means the velocity changes at
the same rate. Non-uniform acceleration
means velocity does not change at
a uniform rate.
What is the direction of the
acceleration vector?
If an object is moving in a line
and its speed is increasing, the change in velocity is positive. The
acceleration in this case is adding to the velocity and is considered
to be positive and in the same direction as then velocity vector.
What happens when you pedal faster on a bicycle?
I
|
Table 1
|
|
Table 2
| ||
|
Time (s)
|
Velocity (m/s)
|
|
Time (s)
|
Velocity (m/s)
|
|
0
|
0
|
|
0
|
8
|
|
1
|
2
|
|
1
|
6
|
|
2
|
4
|
|
2
|
4
|
|
3
|
6
|
|
3
|
2
|
|
4
|
8
|
|
4
|
0
|
Which one of these tables represent positive acceleration?
f an object is moving in a line and its speed is decreasing, the change in velocity is negative. The acceleration in this case is reducing the velocity and is considered to be negative and in the opposite direction as then velocity vector. What happens when you apply the brakes on a car?
Check your understanding
1. In everyday life, you come
across a range of motions in which
- Acceleration is in the direction of motion
- Acceleration is against the direction of motion
- Acceleration is uniform
- Acceleration is non-uniform
Can you identify examples?
2. Starting from a stationary
position, Rahul pedals his bicycle to attain a velocity of 6 m/s in
30 seconds. Then he applies the brakes in such a way that the
velocity of the bicycle comes down to 4 m/s in the next 5 seconds.
Calculate the acceleration of the bicycle in both the cases.
Acceleration on a freely
falling body
One example of uniform
acceleration is acceleration due to gravity. The force of gravity
acts on all objects and they will accelerate downwards if they are
allowed to fall. For a freely falling object, this uniform downward
acceleration is called acceleration due to gravity and is
given by 9.8 m/s2. For a freely falling object, what will
happen to the velocity as it falls, ignoring any air resistance?
Graphs to represent the above quantities
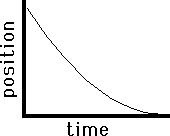
Distance time graphs
So far, we have examined several
terms concepts associated with one dimensional motion. It is easier
to represent all these relationships in graphs. Motion can be
represented as line graphs.
T
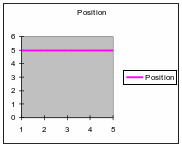
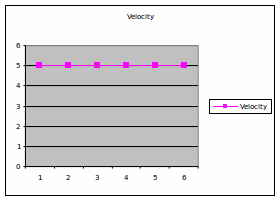
he position of the object is plotted for time from 0 to 5 seconds. The position is at 5 units all through the 5 seconds.
Has the object moved?
What is its velocity?
C
onsider
the object below.
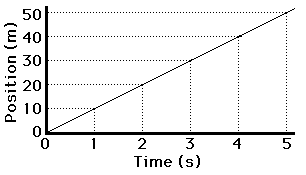
It is covering 0 to 50 m in a
time span of 0 – 5 seconds.
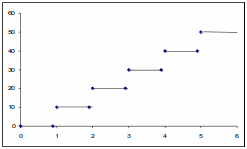
The object is staring from 0;
jumps to 10 m at t = 1 second and stays there till t = 2 seconds;
jumps upto 20 m at t = 2 seconds and so on.
Instead of jumping in steps if
the object were to move continuously, the position time graph would
like the one below.
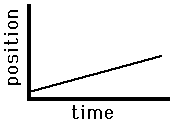
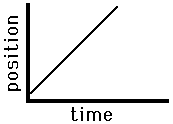
A
straight line means a uniform slope.
Slope
= y2 – y1 / x2 = x1
=
change in position/ change in time
=
velocity
The
object is covering equal distances in equal intervals of time; what
can you say about the velocity?
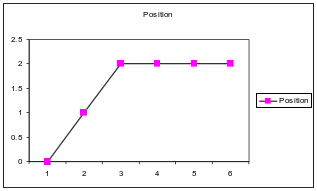
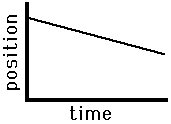
In this graph, the object is
moving uniformly till t = 3 seconds, when it covers a distance of 2
m. After that, it stays at rest.
Can there be a position – time
graph parallel to the y-axis? Why or why not?
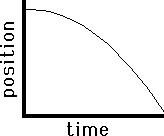
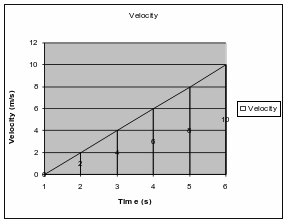
Consider
the object below.
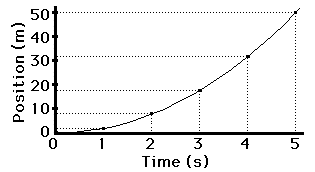
T
he
object here is moving from position 0 m to 50 m in 5 seconds. But it
is not covering the same distance in each second.
Slope
= (y2 – y1 )/ (x2 - x1 )
= change in position/ change in
time = velocity
The
rate at which the position is changing is not constant.; this means
that the slope at different points is different. What can you say
about the velocity?
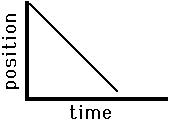
Can
you interpret the following position time graphs?
|
|
|
|
|
|
|
|
|
|
|
|
Velocity - time graphs
In a similar manner, we can also
plot velocity time graphs to describe motion of a body.
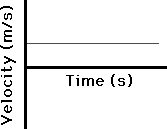
E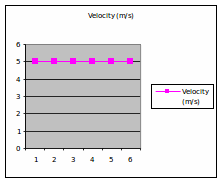
xamine
the graph below. What can you say about the motion? Is the body
moving?
Short quiz :
What is the displacement of the
body at the end of 3 seconds?
- 5
- 15 m
- Can’t say – not enough information
The
graph describes the motion of a body which moves at a constant
velocity. At each second, the body covers 5m. Therefore, at the end
of 3 seconds, the displacement would be 15 m.
Examine
carefully the position – time information below.
Can
you draw a velocity-time graph?
What
can you say about the velocity of this body?
Is
it uniform, increasing or decreasing?
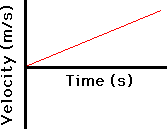
Now,
let us consider the position – time information below.
What
can you say about the velocity of this object? The velocity is
increasing with time. The slope of this graph is calculated as
Slope
= (v2 – v1)/ (t2 – t1)
=
acceleration
If
the slope is the same at all points, we have a case of uniform
acceleration. If the slope is uniform and zero, we have a case of
uniform, zero, acceleration, which means constant velocity. If the
slope is different at different points, we have variable velocity.
|
Positive velocity; constant slope = 0
|
Positive velocity; constant slope
|
|
|
|
|
Acceleration =
|
Acceleration =
|
What can you say about the acceleration in the two graphs above?
When
the acceleration is negative, how will the velocity – time graph
look like?
Check
your understanding
1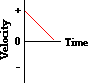
.
Consider the graph at the right. The object whose motion is
represented by this graph is ... (include all that are true):
- moving in the positive direction.
- moving with a constant velocity.
- moving with a negative velocity.
- slowing down.
- speeding up.
- moving with a positive acceleration.
- moving with a constant acceleration.
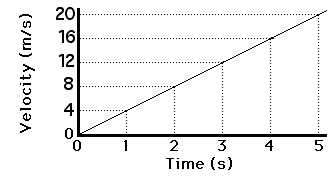
- The velocity of a moving car is recorded at various instants as follows. Can you plot the velocity – time graph?
|
Time
|
Velocity (m/s)
|
|
0
|
0
|
|
5
|
9
|
|
10
|
18
|
|
15
|
27
|
|
20
|
36
|
|
25
|
45
|
|
30
|
54
|
From this data, can you calculate the distance traveled by the car?
Distance
from a velocity – time graph
Consider
the following graphs.
|
|
|
|
|
|
The
motion of any body with an uniform acceleration can be described
starting from the above two equations.
s
= (u + v) * t / 2
a =
(v – u)/ t
Starting
from these two equations and re-arranging, we get the following
equations.
s =
ut + ½ at2
s =
vt – ½ at2
v2 =
u2 + 2as
Convince yourself by deriving
these equations !!!
Can
you complete the following table?
|
|
Distance – time
|
Velocity – time
|
|
Straight line
|
|
|
|
Not a straight line
|
|
|
|
Straight line sloping upwards
|
|
|
|
Straight line sloping upwards
|
|
|
What you should understand at the
end of this chapter?
- Motion is a change of position. It can be described in terms of the distance moved or displacement.
- The motion of an object could be uniform or non-uniform depending on whether its velocity is constant or changing.
- The speed of an object is the distance covered per unit time and velocity is the displacement per unit time
- The acceleration of an object is the change in velocity per unit time.
- Uniform and non-uniform motions of objects can be shown through graphs.
- The motion of an object moving at uniform acceleration can be described with the help of the following equations.
s = (u + v) * t / 2
a = (v – u)/ t
s = ut + ½ at2
s = vt – ½ at2
v2 = u2 +
2as
Check your understanding
- A bus starting from rest moves with a uniform acceleration of 0.1 m/s2 for 2 minutes. Find the (i) speed acquired and (ii) the distance traveled.
- A train is traveling at a speed of 90 km/h. Brakes are applied so as to produce a uniform acceleration of -0.5 m/s2. Find how far the train will go before it is brought to rest.
- A trolley while rolling down an inclined plane has an acceleration of 2 cm/s2. What will its velocity 3 seconds after the start?
- A racing car has a uniform acceleration of 4 m/s2. What distance will it cover in 10s after the start?
- A stone is thrown vertically upward with a velocity of 5 m/s. If the acceleration of the stone is 10 m/s2 in the downward direction, what is the maximum height the stone will go up to? How long will it take to reach that height?
- A driver of a car traveling at 52 km/h applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 seconds. Another driver going at 3 km/h in another car applies his brakes slowly and stops in 10 seconds. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars traveled farther when the brakes were applied?
- S
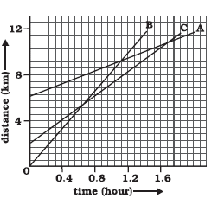tudy the graph and answer the following questions.
- Which of the three is traveling the fastest?
- Are all three ever at the same point on the road?
- How far has C traveled when B passes A?
- How far has B traveled by the time it passes C?
- The speed time graph of a body is given.
- F
ind out how far the car travels in the first 4 seconds. Shade the area on the graph that represents the distance traveled by the car during the period. - Which part of the graph represents uniform motion of the car?
