Difference between revisions of "Frustum of Cone"
(Created page with " === Objectives === Content objectives - what content areas Skill objectives - what specific skills Classroom objectives - to demo peer learning, to make a classroom resour...") |
m (added Category:Mensuration using HotCat) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
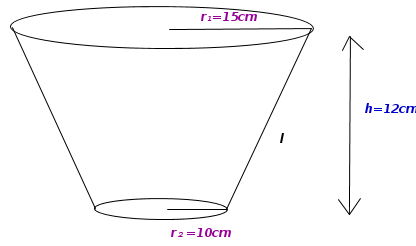
| + | *A bucket in the shape of a frustum with the top and bottom circles of rarii 15cm and 10cm. Its depth is 12cm. Find its curved surface area and total surface area. | ||
| + | (Express the answer in terms of π) | ||
| − | == | + | [[Image:frustum of cone.png|link=http://karnatakaeducation.org.in/KOER/en/index.php/File:Frustum_of_cone.png]] |
| − | + | *Statement of the problem | |
| + | A bucket in the shape of a frustum with the top & bottom circles of radii 15cm and 10cm Its depth(height) is 12cm .CSA & TSA to be calculated length of frustum to be found. | ||
| + | *Assumptions | ||
| + | #Student should know CSA & TSA of frustum of cone | ||
| + | #Student should know the value of л=22/7 | ||
| + | #Student should know the difference between radius , height(depth),lenght | ||
| + | #Student should know the proper substitution simplification | ||
| + | Concepts to be taught | ||
| + | #Lenght of frustum l= | ||
| + | #CSA & TSA of frustum of cone | ||
| − | + | Gaps | |
| + | #difference between radius , height(depth) and lenght | ||
| − | + | Skills | |
| + | #To imagine the frustum of a cone having unequal circles at the top & bottom. | ||
| + | #To imagine that the frustum a cone is having height(depth) inside & length out side. | ||
| + | Algorthem | ||
| + | *Part-01 | ||
| + | #To calculate the Lenght of frustum | ||
| + | given:<math>r_{1}</math>=15cm,<math>r_{2}</math>=10cm, h=12cm | ||
| − | + | Lenght of frustum l=<math>\sqrt{h^2+(r_{1}-r_{2})^2}</math> | |
| − | = | + | l=<math>\sqrt{12^2+(15-10)^2}</math> |
| − | = | + | l=<math>\sqrt{144+5^2}</math> |
| − | = | + | l=<math>\sqrt{144+25}</math> |
| − | |||
| − | |||
| − | + | l=<math>\sqrt{169}</math> | |
| − | + | l=13cm | |
| − | + | *Part-02 | |
| + | #To calculate CSA | ||
| + | CSA= <math> π(r_{1}+r_{2})l</math> Where l=<math>\sqrt{h^2+(r_{1}-r_{2})^2}</math> | ||
| − | + | CSA=<math>π(15+10)13</math> | |
| + | |||
| + | CSA=<math>25 X 13 X π</math> | ||
| + | |||
| + | CSA=<math>325πcm^2</math> | ||
| + | #To calculate TSA | ||
| + | TSA= <math>π({(r_{1}+r_{2})l+r_{1}^2+r_{2}^2})</math> | ||
| + | |||
| + | TSA =<math>π({(15+ 10) 13 +15^2+10^2})</math> | ||
| + | |||
| + | TSA = <math>π({25X13 + 225 + 100})</math> | ||
| + | |||
| + | TSA = <math>({325 + 225 + 100})π</math> | ||
| + | |||
| + | TSA =<math>650πcm^2</math> | ||
| + | |||
| + | [[Category:Mensuration]] | ||
Latest revision as of 08:52, 31 October 2019
- A bucket in the shape of a frustum with the top and bottom circles of rarii 15cm and 10cm. Its depth is 12cm. Find its curved surface area and total surface area.
(Express the answer in terms of π)
- Statement of the problem
A bucket in the shape of a frustum with the top & bottom circles of radii 15cm and 10cm Its depth(height) is 12cm .CSA & TSA to be calculated length of frustum to be found.
- Assumptions
- Student should know CSA & TSA of frustum of cone
- Student should know the value of л=22/7
- Student should know the difference between radius , height(depth),lenght
- Student should know the proper substitution simplification
Concepts to be taught
- Lenght of frustum l=
- CSA & TSA of frustum of cone
Gaps
- difference between radius , height(depth) and lenght
Skills
- To imagine the frustum of a cone having unequal circles at the top & bottom.
- To imagine that the frustum a cone is having height(depth) inside & length out side.
Algorthem
- Part-01
- To calculate the Lenght of frustum
given:=15cm,=10cm, h=12cm
Lenght of frustum l=
l=
l=
l=
l=
l=13cm
- Part-02
- To calculate CSA
CSA= Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle π(r_{1}+r_{2})l} Where l=
CSA=Failed to parse (syntax error): {\displaystyle π(15+10)13}
CSA=Failed to parse (syntax error): {\displaystyle 25 X 13 X π}
CSA=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 325πcm^2}
- To calculate TSA
TSA= Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle π({(r_{1}+r_{2})l+r_{1}^2+r_{2}^2})}
TSA =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle π({(15+ 10) 13 +15^2+10^2})}
TSA = Failed to parse (syntax error): {\displaystyle π({25X13 + 225 + 100})}
TSA = Failed to parse (syntax error): {\displaystyle ({325 + 225 + 100})π}
TSA =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 650πcm^2}