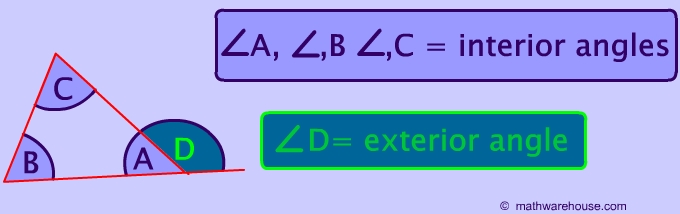Difference between revisions of "Triangles"
| Line 665: | Line 665: | ||
= References = | = References = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 07:13, 22 January 2013
Introduction
The following is a background literature for teachers. It summarises the things to be known to a teacher to teach this topic more effectively . This literature is meant to be a ready reference for the teacher to develop the concepts, inculcate necessary skills, and impart knowledge in Triangles from Class 6 to Class 10. The idea is to know that a triangle is one of the basic shapes of geometry and how a triangle is formed. To understand the type of Triangles based on their sides and angles. To understand how a exterior angle is formed and the meaning of interior angles of a triangle. To know when two triangles become congruent to each other by understanding the postulates. Meaning of similarity and theorems based on similarity of triangles. Costruction of triangles and to find the Area of the Triangle.
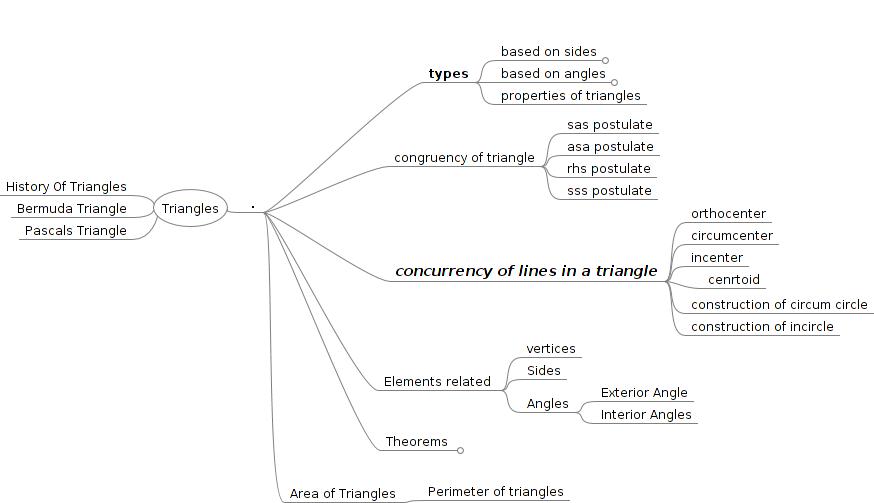
Concept Map
TRIANGLES
Mark three non-collinear point P, Q and R on a paper. Join these pints in allpossible ways. The segments are PQ, QR and RP. A simple close curve formed by these three segments is called a triangle. It is named in one of the following ways.
Triangle PQR or Triangle PRQ or Triangle QRP or Triangle RPQ or Triangle RQP .
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments.
In fact, it is the
polygon with the least number of sides.
A triangle PQR
consists of all the points on the line segment PQ,QR and RP.
The three line segments, PQ, QR and RP that form
the triangle PQ, are called the sides of the triangle PQR.
Angles:
A triangle has three angles. In figure, the three
angles are ∠PQR ∠QRP and ∠RPQ
Parts of triangle:
A triangle has six parts, namely, three sides,PQ
QRand RP.Three angles ∠PQR ∠QRP and ∠RPQ. These are also known
as the elements of a triangle.
Vertices of a Triangle
The point of
intersection of the sides of a triangle is known as its vertex. In
figure, the three vertices are P, Q and R. In a triangle, an angle is
formed at thevertex. Since it has three vertices, so three angles are
formed. The word triangle =tri + angle ‘tri’ means three. So,
triangle means closed figure of straight lines having three angles.
Evaluation
Self-Evaluation
Further Explorations
- [[1]] All about Triangles
Enrichment Activities
Activities
Activity 1: Identifying and Naming Triangles
Learning Objectives
Identify and name the triangles
Material and Resources Required
Pre-requisites/Instructions
Identify and name the triangles in the following Figure.
Evaluation
- Is it possible to construct a triangle with 3 collinear points?
- Is it possible to construct a triangle whose sides are 3cm, 4cm and 9cm. Give reason.
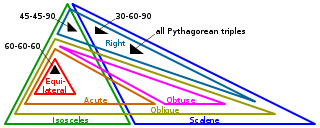
Classification of Triangles
Triangles can be classified in two groups:
Triangles
differentiated on the basis of their sides.
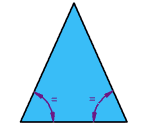
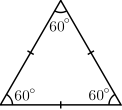
Equilateral Triangles:
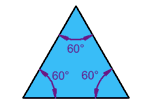 A triangle with all sides equal to one another is called an
equilateral triangle.
A triangle with all sides equal to one another is called an
equilateral triangle.
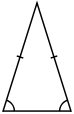
Isosceles Triangle:
A triangle with a pair of equal sides is called an isosceles triangle.
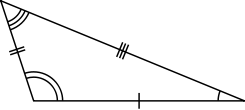
Scalene Triangle:
A triangle in which all the sides are of different lengths and no two sides are equal, the triangle is called a scalene triangle.
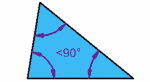
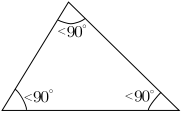
Triangles differentiated on the basis of their angles.
Acute angled triangle.
A triangle whose all
angles are acute is called an acute-angled triangle or simply an
acute triangle.
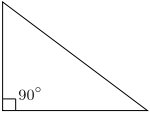
Right Triangles :
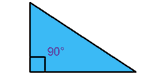 A
right triangle has one angle 90°
A
right triangle has one angle 90°
|
|
|
Right Isosceles Triangle :
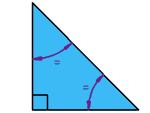 Has
a right angle (90°), and also two equal angles
Can you guess what
the equal angles are?
Has
a right angle (90°), and also two equal angles
Can you guess what
the equal angles are?
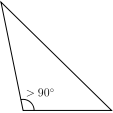
The Obtuse Triangle :
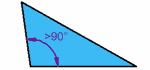 The
Obtuse Triangle has an obtuse angle (an obtuse angle has more than
90°). In the picture on the left, the shaded angle is the obtuse
angle that distinguishes this triangle
The
Obtuse Triangle has an obtuse angle (an obtuse angle has more than
90°). In the picture on the left, the shaded angle is the obtuse
angle that distinguishes this triangle
Since the total degrees in any triangle is 180°,
an obtuse triangle can only have one angle that measures more than
90°.
Interior angles of a triangle
The interior angles are those on the inside of the triangle.
Exterior Angles of a triangle
An exterior angle is formed by extending any side of the triangle.
Summary of triangle centres
There are many types of triangle centers. Below are four of the most common.
|
Incenter
|
|
Located at intersection of the angle bisectors. See Triangle incenter definition
|
|
Circumcenter
|
|
Located at intersection of the perpendicular bisectors of the sides. See Triangle circumcenter definition
|
|
Centroid
|
|
Located at intersection of medians. See Centroid of a triangle
|
|
Orthocenter
|
|
Located at intersection of the altitudes of the triangle. See Orthocenter of a triangle
|
In the case of an equilateral triangle, all four of the above centers occur at the same point.
The Incenter of a
triangle
Latin: in - "inside,
within" centrum - "center"
The point where the
three angle bisectors of a triangle meet.
One of a triangle's
points of concurrency.
Try this Drag the
orange dots on each vertex to reshape the triangle. Note the way the
three angle bisectors always meet at the incenter.
One of several centers the triangle can have, the
incenter is the point where the angle bisectors intersect. The
incenter is also the center of the triangle's incircle - the largest
circle that will fit inside the triangle.
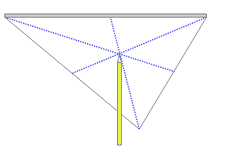
Centroid of a Triangle
From Latin: centrum - "center", and Greek: -oid -"like" The point where the three medians of the triangle intersect. The 'center of gravity' of the triangle One of a triangle's points of concurrency. Try this Drag the orange dots at A,B or C and note where the centroid is for various triangle shapes.
Refer to the figure . Imagine you have a
triangular metal plate, and try and balance it on a point - say a
pencil tip. Once you have found the point at which it will balance,
that is the centroid.
The centroid of a triangle is the point through which all the mass of a triangular plate seems to act. Also known as its 'center of gravity' , 'center of mass' , or barycenter.
A fascinating fact is that the centroid is the
point where the triangle's medians intersect. See medians of a
triangle for more information. In the diagram above, the medians of
the triangle are shown as dotted blue lines.
Centroid facts
- The centroid is always inside the triangle
- Each median divides the triangle into two smaller triangles of equal area.
- The centroid is exactly two-thirds the way along each median.
Put another way, the centroid divides each median into two segments whose lengths are in the ratio 2:1, with the longest one nearest the vertex. These lengths are shown on the one of the medians in the figure at the top of the page so you can verify this property for yourself.
Orthocenter of a Triangle
From Greek: orthos - "straight, true, correct, regular" The point where the three altitudes of a triangle intersect. One of a triangle's points of concurrency.
Try this Drag the
orange dots on any vertex to reshape the triangle. Notice the
location of the orthocenter.
The altitude of a triangle (in the sense it used here) is a line which passes through a vertex of the triangle and is perpendicular to the opposite side. There are therefore three altitudes possible, one from each vertex. See Altitude definition.
It turns out that all three altitudes always
intersect at the same point - the so-called orthocenter of the
triangle.
The orthocenter is not always inside the triangle.
If the triangle is obtuse, it will be outside. To make this happen
the altitude lines have to be extended so they cross. Adjust the
figure above and create a triangle where the orthocenter is outside
the triangle. Follow each line and convince yourself that the three
altitudes, when extended the right way, do in fact intersect at the
orthocenter.
Activity 1 Types of Triangles
Learning Objectives
Be able to identify triangles.
Material and Resources Required
Pre-requisites/Instructions
Identify the types of triangles.
|
|
|
|
|
|
|
|
Evaluation
- Can a scalene triangle also be a right-angled triangle ? If yes can you draw one ?
Activity 2 Similar Triangles
Learning Objective
To show similar planar
figures, discuss congruence and properties of congruent/ similar
triangles
Material and Resources Required
Blackboard
Geogebra files +
projector
Calculator
- Planar figures and triangles
- Draw pairs of figures on the board [ both similar and dissimilar]; they can identify overlap of congruent figures
- Ask the children to identify
- If the children know the names of the theorem, ask them to explain- ask them what is SSS, AAA, ASA
- Show ratio and give the idea of proportionality
- Geogebra files. When I change the sides/ proportion, the triangles change in size. But the proportion remains the same, angle remains the same
- With calculator they verify proportion (this is very very useful for involving the whole class) they all can see the proportion remains constant though the size changes
- Show the arithmetic behind the proportion
Evaluation
[Activity evaluation - What should the teacher watch for when you do the activity; based on what they know change]
- Confusion between congruence and similarity
- When they give the theorem, if they cannot identify included side and angle
- When there is a wrong answer, identify what is the source of the confusion – sides, ratio and proportion
- Direct substitution
Evaluation
Self-Evaluation
Further Explorations
Enrichment Activities
Pythagorean Theorem
Pythagoras' Theorem was discovered by Pythagoras, a Greek mathematician and philosopher who lived between approximately 569 BC and 500 BC.
Pythagoras'
Theorem states that:
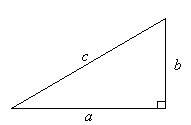
In
any right-angled triangle, the square of the hypotenuse is equal
to the sum of the squares of the other two sides. That is:
Pythagoras' Theorem in
Three Dimensions
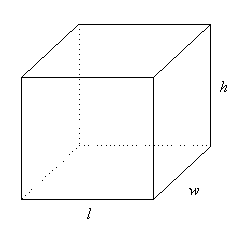
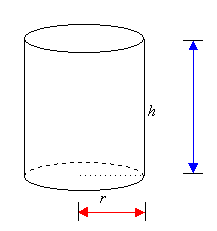
A
three-dimensional object can be described by three measurements -
length, width and height.
We
can use Pythagoras' Theorem to find the length of the longest
straw that will fit inside
the
box or cylinder.
Evaluation
Self-Evaluation
Further Explorations
Enrichment Activities
See Also
Teachers Corner
Sucheta SS doing a lesson on similar triangles using GeoGebra in the classroom