Measurement
Scope of this document
The following note is a background document for teachers. It summarises the things we will need to know. This note is meant to be a ready reference for the teacher to develop the concepts in measurement from Class 6 onwards to Class 10.
This document attempts
to cover all the topics identified in the concept map. To plan the
actual lessons, the teacher must use this in connection with the
theme plan.
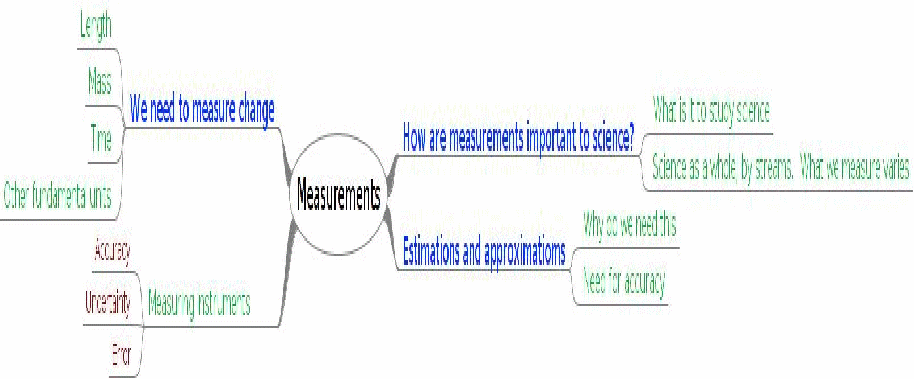
Concept Map
Theme Plan
|
CLASS
|
SUBTOPIC
|
CONCEPT DEVELOPMENT
|
KNOWLEDGE
|
SKILL
|
ACTIVITY
|
|
6
|
Comparison
|
Measurement plays an important role in understanding the world around us. Measurement involves comparison.
|
Length, Time, Mass, Number as various measurements
|
Recognise the different attributes that need to be measured Recognise that some attributes can be measured and some cannot be
|
Activity 1
|
|
7
|
Estimation
|
Understand that an estimation is an important part of measuring Assumptions are made while estimating and these form the basis for estimations
|
Approximations Patterns
|
Identify various methods and approached that can be used
|
|
|
8
|
Standardization
|
There is a need for a standardized unit for measurement Instrument choice depends on precision needs
|
Anecdotal, historical information about various units of measure that were used What are the standard units for mass, length and time
|
Learn to measure with ruler Learn some conversions between the standard and non-standard units
|
Activity 2
|
|
9
|
Conversion
|
Movement from one standard to another (from distance between two points to wavelength as a measure of length standard) and the reasons for these
|
Least Count, Magnitude, Standard form
|
Use of measuring instruments Expressing measurements in units of magnitude
|
Activity 3,4,5
|
|
10
|
Experimentation and measurements
|
Understand that there are properties that are intrinsic - mass, charge, etc. Hence there are fundamental and derived units Understanding error in measurements
|
Measurements with vernier calipers, screw gauge, Significant figures, Physical balance, time measurements for simple pendulum
|
Use of measuring instruments Plotting graphs of the measurements and interpreting the measurements Calculating systematic error Experimenting and recording best-fit values
|
Activity 3,4,5
|
Curricular Objectives
- The students will be introduced to the role of measurements in science and methods of measurement, stanadardization and estimation.
- Various measuring tools will be introduced.
Measurements – An overview
All the branches of science involve recording and measurement. However, Physics involves more quantitative measurements than Chemistry and Biology.
We would look the mathematical basis of Physics
and then at the concept of quantitative measurements.
The mathematical basis in Physics
We had earlier talked about what are the features that characterize a particular branch of study as science or not. We had also seen that what we call as science or non-science is fairly arbitrary. However, there are approaches that can be grouped together as a ‘scientific approach’. A key element in this approach is measurement.
Physics is about measuring and identifying change.
Usually, in Physics, the first chapter is always about measurement.
What do I measure? How do I measure? These questions are posed.
The first step is to understand this emphasis on
measurement in Physics. Why do we give this kind of importance to
measurements? We don’t do this in Chemistry, in Biology. We can
get through large parts of Chemistry and a great deal of biology
without this kind of measurement. What is it about Physics that
makes this necessary?
Of course, the first reason that one could think
of is that if we are to study interactions of matter - the content of
physics – then such interactions can be studied only by observing
the changes brought about. These changes are brought about in space,
over time. If we do not record what changed, by how much and when,
we might not be able to make any progress in our scientific enquiry
as far as Physics goes.
Another important contributor to this emphasis on
measurement is due to parallel developments in mathematics that
facilitated such studies. Interestingly, there is an article by a
scientist called Eugene Wigner titled ‘The unreasonable
effectiveness of Mathematics in Physics’. Physics is almost wedded
to mathematics and would be hugely dysfunctional without it.
Mathematics is the most effective tool in explaining the changes that
we observed due to interactions. Why should this be so?
We must note that prior to the
renaissance and Galileo, Newton et al. mathematics was not the
language of Physics. Greeks and others who studied the natural
sciences (the separation into Physics, Chemistry and biology came
much later and the subsequent fragmentation into various polysyllabic
combinations is a 20th
century invention!) and the theories were based on empirical
observations and opinions; These opinions were very loosely
structured and could not stand the rigor of observations, theory,
tests and experimentation - Ptolemy’s model of the world was based
on pictures, models, not numbers.
Post Galileo, mathematics became the language of
Physics. The idea that you can use numbers, numerical data was
developed from this point on. Scientists of this time -, Galileo and
Kepler – extensively relied on mathematics to explain their
findings. This could have also been possible because of the
developments happening in mathematics.
It could be said that
mathematical predictions of various kinds have been made in other
civilisations and the West has no copyright on this. The Mayans and
their calendar and their predictions of eclipses, the ability of
pacific civilisations to accurately cross thousands of miles of
oceans using stars and ocean currents, Indian predictions of
distances to the sun and a heliocentric theories etc. The difference
is two fold – firstly the 17th
century to date we have followed a logically contiguous and complete
theory (earlier theories were isolated to describing specific
phenomenon and was not an all-encompassing world view) and the
extensive use of mathematics to make predictions and test them
accurately.
We have seen that math is being used extensively,
but why should it be so? After all, mathematics is an invention of
the human mind. It is the invention of one time creature. In a small
planet that is part of a small solar system of an average star, in an
average-sized galaxy. Why should such an invention be so effective
in explaining, predicting what will happen to the universe? The idea
that what I can see in the world can be described in mathematics is
amazing.
We examine some possible reasons for this
effectiveness.
- One limiting answer is to say Physics only looks at those questions which can be answered by mathematics.
- In the way, the universe is, there are patterns, symmetry. Mathematics deals with patterns, symmetry and hence, can explain the universe.
- Availability of increasingly accurate measuring instruments. At some point in time, it became important to measure distance and time accurately. This need was felt more, and acutely, by sailors. Elaborate and accurate instruments were made and fortunes spent to build these measuring instruments. When Galileo made some of his most important measurements and experiments, the most reliable measure of time he had was his pulse!
One could think of other ways of explaining this but the fact is that Physics & mathematics are now inextricably intertwined!
As we can see, this led to a move towards more
precise and accurate measurements. Any science, when explaining
observed phenomena moves, in varying degrees, towards predictions.
For instance, once you can measure time accurately, you can talk of
rate of change. This kind of precision and prediction becomes
possible only with higher level of computational work. Modelling had
been a way of explaining things. When numbers get involved, models
become more predictive. For example, a precise definition of mass as
an intrinsic property was something that was possible only after we
could precisely measure the changes in acceleration and the
dependence of this quantity on the can be inferred only based on
formal based on observations.
When precision becomes important, we become
careful on what we measure and how we measure.
Unit 1 - Concepts in measurements
Comparison and standardisation
We have finally moved to looking at what we call measurements. There are a few quantities which we define as fundamental. What this means that they are the basic elements of information that can be gathered by observation and all other quantities can be derived from these.
It has not always been easy to determine which are
the fundamental units. For example, heat was once considered to be a
fundamental unit. A unit was developed for measuring heat -
calories. It was then found out that heat is a form of energy.
Energy (work done) can be expressed in terms of other fundamental
units and the calorie is used only in a non-scientific context.
On the other hand, temperature is a measure of the
average kinetic energy of an object. It is unique. Charge is unique.
These are all independent quantities. They cannot be expressed in
terms of other quantities.
Now that we know what to measure, how do we go
about it? It was not always that we had a standard unit of measure.
We had fairly arbitrary units of measurement, like yards, feet and so
on.
When there was a move to observe and record
precisely, it becomes important that we make standard measurements.
Why do we need a standard? When we measure something with a
standard, we are essentially using that standard to compare with
another measurement. For instance, when you measure your height with
a metre scale, you are not comparing yourself to the ruler. You will
be comparing your height to another person and the ruler is the tool
that tells you which of you is taller. Comparison between two
quantities is possible only if the measurement is made with respect
to the same object. The metre scale or any standard by itself is
meaningless- it derives its importance from the comparison it allows
us to make.
How should we define these standards?
For a long time, distance (length) was measured in terms of feet, yards (basically space covered). And time was measured as the interval between two events. Till about 300 years ago, the yard was considered a good enough measurement of length. Until about 200 years ago the standard distance was measured as a certain fraction of the distance from the pole to Paris.
Clearly, this process is not satisfactory. These
standards by themselves are not reliable. If you went to bed today
and woke up to find out that everything became twice as long, how
would you know? I would have grown twice as tall, but so would the
metre scale. Using something to measure itself is not a very good
idea.
These days, the standard of
length is measured in terms of time. Length of 1m is measured as the
distance traveled by light in (1/299,000,000)th of a second. Time
is measured in terms of number, the number of
oscillations of a Cesium atom. The only thing that we cannot measure
like this is in the case of mass.
We cannot measure mass in terms of something else;
the peculiar problem is that mass keeps changing as atoms and
molecules diffuse in and out of any object and the loss or gain of
matter will result in a change of mass. Miniscule, as it might be,
the mass would be different. For mass alone we have multiple
standards of platinum-iridium alloy that are maintained at various
places and these are compared to determine the standard for
kilogramme.
In the case of temperature, we define an absolute
zero. This is a theoretical construct, the temperature at which all
molecules will stop vibrating. This is not physically possible to
achieve. However, we define the triple point of water at a
particular pressure and temperature (solid, liquid and gas co-exist)
as a standard 273.15K. In the case of a regular thermometer, we use
pressure to measure temperature. While charge is a fundamental unit,
we define 1 C of charge in terms of the current flowing and time.
This is so because it is easier to measure current than charge.
Various units of measurement
All these various units of measurement come about
based on what you want to measure. For example, mm, cm, dm, have all
come up because of how I want to use it. It is important to know why
they are there even if I don’t know how to calculate using those
units.
It is interesting to wonder why we have mg, mm,
cm, etc. but nothing of a similar magnitude of difference after kg or
km. This is due to our understanding of mass. We have no difficulty
in measuring in the range of 100 kg. Units of measurements are
created because of a felt need. It is good to know that units go in
powers of ten.
Estimation and error
Precision and error are very important in the context of measurement. I would also add estimation to this list. What is the difference between these three?
Estimation
Let us say we want to find out the mass of one
strand of hair. One way of estimating would be think of hair
clippings (when you cut your hair) and estimate its mass. Based on
this and an estimate of quantity we can work out an answer which is
right within an order of magnitude. Is this reasonable? Is it
likely to be correct? The answer to this question is yes if our
result is within an order of magnitude.
To be able to work with known things and find out
the unknown is estimation. Estimation is about a way of thinking.
When we estimate, the order of magnitude becomes important.
For example, let us estimate
the mass of the Earth. What would I start with? I would start with
the radius of the Earth and calculate the volume. To find the mass
of the Earth, what do I need if I know the volume? We need density.
We know that water density is 1000 kg/m3.
Let us say that the earth is at least ten times as denser.
M = Volume x density
= (4/3) x 3.14 x (6.4 x 103x
103)3
x 10 x 1000 = of the order of
magnitude 1024
Error
– It can very loosely be defined as a mistake.
The first kind of error could be a
zero error. For example, let us say we have a measuring tape with
kinks in it. It will show a longer length than is actually there.
These are errors due to the error in the measuring instrument.
Similarly, in the case of a spring balance, it is
possible that the extension the spring has between 1000 to 1100kg is
more than the extension from 100 g to 200g. If I know that this
error exists, I can adjust for it. These kinds of error can be
corrected if we know the nature of the error and we are able to
quantify the error – even if the computation is very complex.
For instance, there are distortions in the images
captured by the Hubble Telescope because of the curvature of the
mirror used in it. Once this was identified, the solution consisted
of adjusting the data obtained to account for the instrument error.
To verify that the adjustment was correct, the corrected images from
the Hubble were verified with images from other telescopes
Another kind of error in measurements is due to
statistical error. These errors follow what is called a normal
distribution. In other words, there is an equal likelihood
(probability) of the recording deviating on either side of the
average value. When a large number of readings are taken, this error
is averaged out as the deviation, in the average, would be the same
on both sides of the correct value.
Standardization - How to use different units
(Appendix 1 and 2 give more information about the history of SI and the powers of ten)
Unit 1 – Comparison, standardisation and SI units
- The necessity for measuring various quantities was felt since medieval times and the need for uniform standards was also understood. Standards and instrumentation have evolved over a period of time and some of the older units are still used.
- Measurement without tools is difficult.
- Measurements have evolved over time and how we have moved from inaccurate and human centred measures to more objective and independent standards. Learning outcome here is the idea of how discoveries and processes take place rather than absolute facts themselves.
- Absolute measurements are not possible without using tools. Relative measurements are possible but the scope for error is high and in some cases it may not be very practical. Indirect measurements will be possible in some cases. In case of relative measurements, the measures are qualitative rather than quantitative and hence difficult to communicate to others or replicate
- During standardization efforts, originally the day was to be subdivided decimally. This failed to catch on, in part because people thought it would make their expensive clocks obsolete. Hence we continue with what it was prior to this.
- Area and volume are derived units. Area can be simply looked at as the region enclosed by two lengths and hence it is represented by m2. Similarly, Volume can be simply looked at as the space enclosed by three lengths and hence is represented by m3.
- Scientific notation for representing very large/small numbers discussed. Ease of arithmetic with scientific representation to be briefly discussed.
- Mass measurements can be made for an electron or for earth or anything in between.
- Length measurements range from an electron size to celestial distances. A light year may be introduced here. (Speed of light is about 300,000 KM/sec. Light year is about 9.461×10^12 km or 9.461×10^15 m)
- Time measurements in terms of hours/years/decades/etc. Are common. Very low or high values of time are used by scientists and astronomers.
- Temperatures follow the natural number representation. They do not have large variations in practical applications and hence the prefixes are rarely used.
- Numbers could range from –infinity to +infinity.
- Detailed learning outcomes would involve the following
Key Vocabulary
The International System of Units (SI) is a modernized version of the metric system established by international agreement that provides a logical and interconnected framework for all measurements in science, industry and commerce. This system is built on a foundation of seven base units and all other units are derived from them.
Base
unit for Length is Meter (M)
Up until 1983
the meter was defined as 1,650,763.73 wavelengths in a vacuum of the
orange-red line of the spectrum of krypton-86. And since then it is
determined to be the distance travelled by light in a vacuum in
1/299,792,45 of a second.
Base unit
for Time is Second (S)
The second is
defined as the duration of 9,192,631,770 cycles of the radiation
associated with a specified transition of the cesium-133 atom.
Base unit
for Mass is Kilogram (KG)
The standard
for the kilogram is a cylinder of platinum-iridium alloy kept by the
International Bureau of Weights and Measures in Paris. A duplicate at
the National Bureau of Standards serves as the mass standard for the
United States. The kilogram is the only base unit defined by a
physical object.
Base unit
for Temperature is Kelvin (K) and °Celsius (°C)
The Kelvin is
defined as the fraction 1/273.16 of the thermodynamic temperature of
the triple point of water; that is, the point at which water forms an
interface of solid, liquid and vapour. This is defined as 0.01 °C on
the Celsius scale and 32.02 °F on the Fahrenheit scale. The
temperature zero K (Kelvin) is called "absolute zero".
Base unit
of Electric current is Ampere (A)
The ampere is
defined as that current that, if maintained in each of two long
parallel wires separated by one meter in free space, would produce a
force between the two wires (due to their magnetic fields) of 2 x
10-7 N (Newton) for each meter of length. (a Newton is the unit of
force that, when applied to one kilogram mass would experience an
acceleration of one meter per second, per second).
Base unit
of Luminous Intensity is Candela (C)
The candela
is defined as the luminous intensity of 1/600,000 of a square meter
of a cavity at the temperature of freezing platinum (2,042 K).
Base unit
of Amount of Substance is Mole (mol)
The mole is
the amount of substance of a system that contains as many elementary
entities as there are atoms in 0.012 kilogram of carbon-12.
Advantages of the SI:
- There are only 7 basic units and all others are derived units of these seven units.
- The SI unit changes in magnitude in powers of 10 only and a unique prefix may be added to the unit to indicate the power. For example, kilo- denotes a multiple of a thousand and milli- denotes a multiple of a thousandth; hence there are one thousand millimetres to the metre and one thousand metres to the kilometre. The prefixes are never combined: a millionth of a kilogram is a milligram not a micro kilogram. The other powers are provided in the table at Annexure.
Unit 2 – Estimations
Students will understand the significance of estimations in daily life, the requirements and relevance of accuracy of projections, learn to relate the known factors to the unknown and learn how our assumptions affect accuracy.
Different estimation methods are available. The estimations are by no means exact. The process needs to be validated rather than the answer. The assumptions can vary with each individual trying to solve the problem and the answers obtained are good enough for the assumptions made. When the assumptions are replaced by known data the process will yield ‘good answers’.
What is estimation?
Estimation is the process of guessing an approximate value of a number. An estimation process is initiated when a problem is presented with information that seems too meagre to help arrive at a quantitative result. The process of estimation requires one to ask questions to get different ways leading to the end result.
Why estimate?
It is a very important life skill and hence it is important to understand it. Estimations are very helpful in the following 3 scenarios.
- An exact value of a quantity is impossible to obtain – for example, the number of stars in our galaxy, number of sand grains in a stretch of beach, number of fishes in the ocean, etc.
- An approximate value is adequate – for example, the number of people attending a party, budgetary estimates for a trip, travel time between the Valley and BIAL, etc.
- An approximation serves as a rough check of the accuracy of a measurement – for example, you computed 23x45 and got 10035, the clock shows 11.30 at sun set, the weighing scale indicates your weight as 10 KG, etc.
How to estimate?
The following step by step approach is to be used for estimation.
Depending on the nature of the estimation problem, any of the
following methods may be used for identifying the possible
approaches.
The various methods are given below. Appendix 3 gives the details of the Fermi approximation.
Estimation Method 1:
To find the height of a room, a person with some knowledge of standard measures and experience, could just look at the room and mentally map it with respect to a known height, say to that of a ruler or another person, and estimate how high the ceiling is. Similar guesses are possible about whether a dress size fits a person, whether the day’s news paper looks unusually bulky or thin, etc. This is an educated guess or an eyeball estimate.
Estimation Method 2:
To find the length and width of a corridor, it is easier to find and count parts rather than estimate the whole directly. We identify one part such as a floor tile or wall tile, estimate or count how many such units make the length/width, then multiply the number with the basic dimensions to get the measure. This method can be effectively used for estimation requirements such as finding the number of marbles in a jar, number of street lights in a highway, number of sheets in a book, etc. This estimation method is called the sampling method.
Estimation Method 3:
To solve problems which are beyond visualization and where absolutely no data is available, we estimate by analysis, approximations and assumptions. This approach helps us to arrive at a process for estimating the problem. Fermi specialized in this method - Teachers to read annexure F to understand Fermi’s approach to solve an estimation problem – this can be shared with the children.
Method 4:
Some problems can be estimated by a combination of the above methods.
Illustration of an estimation method # 1
Problem statement: Estimate how much of drinking water is consumed at the Valley School on a typical working day.
The single source of drinking water is the water purifier at the
dining hall. The water used for drinking from here will be estimated.
The water consumption is represented in litres. All the pots in
various parts of the school are filled from here. During lunch and
snack, students will drink from the dining hall pot. But usually
buttermilk and juice are drunk instead of water.
Possible approaches:
One approach could be top-down, trying to figure out how much of
water is purified for drinking purpose every day. That is if the
duration for which water purifier is in operation and the rate of
water output are known, then the water consumed can be computed. For
example, if the drinking water output is about 5 litres/minute (based
on observation or by referring to the purifier manual) and if the
purifier is in operation for about 2 hours a day (based on
observation), then the water consumption can be assumed to be about
5*2*60 litres = 600 litres. In this approach, the calculations
carried out thus far would appear fairly accurate. However, all the
water that is collected from purifier may not be consumed entirely. A
percentage of consumption will have to be assumed to refine the
estimate – which could be hard to get without more
analysis/information.
The other approach could be bottom-up analysis.
The following assumptions are made:
Calculations:
Water consumed from pots = (20*10)*(2/3) = 160 litres (approx).
Water consumed at the dining hall = (500 * 200)/1000 = 100 litres.
Total drinking water consumption = 260 litres/day.
This estimate gives an idea of the amount consumed. It also indicates that an available capacity of about 50% more than this amount would be sufficient to ensure that all pots/jugs are filled every day.
As assumptions are listed, the impact of change in assumptions is
clear.
Illustration of an estimation method #2
Student groups to solve the following problem in class or as home work.
Problem: If the science note books are stacked in one of the middle
school classroom – end to end and floor to roof – how many note
books would be required to fill the room?
Problem: If the science note books are stacked in one of the middle school classroom – end to end and floor to roof – how many note books would be required to fill the room?
More
clear definition of the problem: The books are to be stacked
horizontally and not vertically and the books are stacked as high as
the height of the walls and not to the height up to the middle of the
roof (which is higher than the wall height). The estimation will
indicate the number of books that can be stacked.
Approach
to solution:
- Estimate the outer dimensions of a notebook are x, y and z cm/mm.
- Estimate the corresponding dimensions of the room to be filled are X, Y and Z m/cm.
- Decide whether the books should be placed lengthwise against the length of the room or breadth wise against the length of the room or a combination, so as to place the maximum number of books per layer. Arrive at a mathematical calculation to compute the number of books per layer.
- Estimate the number of vertical layers.
- Arrive at the mathematical calculation to compute the total number of books.
Unit 3 : Actual process of measurement with various tools
Expected learning
Children learn to use right tool for any measurement. They will learn to write their observations in a coherent way. They will learn to gather data, interpret the same using different graphical notation. The teacher can demonstrate the following:
- Measure volume using a graduated beaker
- Measure the thickness of the glass beaker.
- Measure the thickness of the thread.
- Measure the length of the table
Additional Resources
- Videos: Real world_ US standard of measurement vs Decimal system. [[1]] [[2]]
- Various measuring tools according to the activity. Measuring tape, small ruler and long ruler, meter scale, running meters of cloth, string, Slide calipers, and Screw gauge, glass beaker, roll of thread.
- [[3]]
- [[4]]
Activities
Activity 1
Objective:
To understand the process of comparison
Procedure
- Homework: Take a handful of any (Wheat/Rice/Barley/Jowar/Ragi) grain. Observe their size. Do they vary a lot in size and weight? Write a few lines about your observation. Classwork activity 1:
- Compare the mass of 6 different objects made of different materials and of different shapes. Teachers to identify 6 objects weighing around 100 grams. Children to feel the relative weights of the objects by holding them on hand. Then children should write the names of the 6 objects in their notebooks in ascending order of their weights. If children can guess the weight of the object, let them write it too – children are sure to have different opinions of the relative weights of each object. Also they cannot guess the correct weight without a tool to measure. (The 6 objects selected are placed in the increasing order of weights – Spice pack, Green plastic tray, Book, Cotton, Stainless steel plate and Soap). Classwork activity 2:
Discussion questions for the class
- What are the difficulties in measuring like this?
- Can you tell others what your measurement is?
- When we measure, what do we do (comparison)?
- Why is comparison difficult without a tool?
- Can I measure how big (the area) a notebook page is or how large (volume) of a beaker? What measure do I need first? (Length is a fundamental unit)
Evaluation
(fill in the
blanks)
- There are over 20,000 living species of fish. They range in size from 7.9 Millimetres (Paedocypris that lives in tropical swamps in Sumatra) to 14 Metres (whale shark).
- Dinosaurs are extinct land reptiles of the Mesozoic era. The dinosaurs, which were egg-laying animals, ranged in length from 91 Centimetres to 39 Metres. Recognized discoveries of fossilized dinosaur bones date only to the 1820s; Sir Richard Owen, a Victorian anatomist, coined the term dinosaur.
- African bull elephants may reach a shoulder height of 4 Metres and weigh up to 8000 Kilograms. Their tusks are more than 3 Metres long and weigh up to 90 Kilograms each. Females are somewhat smaller and have more slender tusks. African elephants have enormous ears, measuring up to 107 Centimetres in diameter. The Indian bull elephant reaches about 2.7 Metres in shoulder height and weighs about 3200 Kilograms; its tusks are up to 180 Centimetres long.
- Light travels at a speed of 300,000 KM/ Second. The minimum distance between earth and sun is 146,000,000 Kilometres and the maximum distance is 152,000,000 Kilometres. Hence the sun light takes about 8 Minutes to reach from sun to earth.
- My mother said that our normal body temperature is 98.6 degrees and my friend says that it is usually at 36.85 degrees and my scientist father insists that it is 310 degrees. My father also confirms that all of them are right in their own way. Can you figure out how?
- Answer: 98.6 Degrees Fahrenheit = 36.85 Degrees Celsius = 310 Degrees Kelvin.
- Note: To convert Celsius to Fahrenheit, multiply the Celsius temperature by 9, then divide by 5 and then add 32. OR Multiply Celsius by 1.8 and then add 32.
- Some of the international records for Twenty20 cricket are provided below. Please put in the right units against each number so a novice can also understand.
- The highest team totals are in the range of 200 – 260 Runs while the lowest are in the range of 67-97 Runs. Yuvraj singh holds the Fastest 50 record of 12 Balls while Chris Gayle holds the Fastest 100 record of 50 Balls.
- A few years ago, the price of onion was Rupees 2/Kilogram. It is predicted to go up to Rupees 60/Kilogram in the year 2010. Assuming there are about 20 onions per Kilogram, the price of each onion has gone up from 10 Paise per piece to 3 Rupees per piece.
Activity 2
Objective:
To understand what precision means. These are suggested objects. Identify other appropriate objects based on the students' context. Measure the following dimensions using any tools available at home and write down the values.
|
#
|
What to measure?
|
Value
|
|
1
|
The length of your TV screen
|
|
|
2
|
The breadth of your TV screen
|
|
|
3
|
The depth of your TV
|
|
|
4
|
The height of your chair/ bed
|
|
|
5
|
The breadth of your chair/ bed
|
|
|
6
|
The length of your chair/bed
|
|
|
7
|
The length or diameter of a CD/ DVD
|
|
|
8
|
The thickness of your favourite DVD
|
|
|
9
|
The length or diameter of the smallest button on your TV control or remote
|
|
|
10
|
The length or diameter of the largest button on your TV control or remote
|
|
Activity 3 Using the vernier calipers
Materials : Vernier Calipers, graph sheet, ruler
Procedure:
- On a graph sheet make two scales – one of ten divisions (vernier scale) and the other of 9 divisions (main scale).
- The scale of 9 divisions will have the same length as the scale of 10 divisions.
- Place one scale over the other and explain least count of the vernier callipers.
- Measure the dimensions of an object using the vernier callipers
- Explain the method of calculations and the idea of significant digits.
- Explain zero error and relative error with respect to the instrument.
Activity 4 Using the screw gauge
Materials : Screw gauge
Procedure:
- Measure the dimensions of an object using the screw gauge
- Explain the method of calculations and the idea of significant digits.
Activity 5 Measuring the timer period of a simple pendulum
Materials : Simple pendulum experient set-up, graph sheet
Procedure:
- Measure the time period of a simple pendulum for different lengths
- Record the time period
- Explain how to plot a best fit curve of time period with respect to length
- Extend this to calculate “g” from the graph.
Additional Information - History
From times immemorial different kinds of measurements have been used to describe an object or phenomena or event.
History of Length measurement:
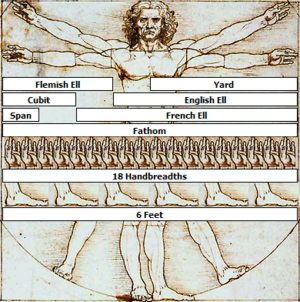
Length has been the most necessary measurement in everyday life, and basic units of length reflect the first elementary methods used by humans. For example, the inch is the width of a thumb. The foot speaks for itself. The yard relates closely to a human pace, but also derives from two cubits (the measure of the forearm). The mile originates from the Latin ‘mille passus’ – meaning a 'thousand paces', approximating to a mile because the Romans define a pace as two steps, bringing the walker back to the same foot. With measurements such as these, it is easy to explain how far away the next village is and to work out whether an object will get through a doorway.
For the complex measuring problems – such as surveying land to register property rights, or selling a commodity by length - a more precise unit was required. The solution was a rod or bar, of an exact length, kept in a central public place. From this 'standard' other identical rods can be copied and distributed through the community. In Egypt and Mesopotamia these standards were kept in temples. The basic unit of length in both these civilizations was the cubit. This was based on the length of a forearm measured from elbow to the tip of middle finger. When a length such as this is standardized, it is usually the king's dimension which is first taken as the norm.
This diagram gives an insight into how the human body could become a reference for units of measurement of length.
History of Mass measurement:
For measurements of mass, the human body provides no such easy approximations as for length. But nature steps in. Grains of wheat are reasonably standard in size. Refer to the outcome of the homework. Mass can be expressed with some degree of accuracy in terms of a number of grains – this is a measure still used by jewellers.
As with measurements of length, a lump of metal can be kept in the temples as an official standard for a given number of grains. Copies of this can be cast and weighed in the balance for perfect accuracy. But it is easier to deceive a customer about mass, and metal can all too easily be removed to distort the scales. An inspectorate of weights and measures is from the start a practical necessity, and has remained so.
History of Time measurement:
Time, a central theme in modern life, has for most of human history been thought of in very imprecise terms. The day and the week are easily recognized and recorded - though an accurate calendar for the year is hard to achieve. The forenoon is easily distinguishable from the afternoon, provided the sun is shining, and the position of the sun in the landscape can reveal roughly how much of the day has passed. By contrast the smaller parcels of time - hours, minutes and seconds - have until recent centuries been both not measurable and not needed.
Sundials have been in use from the 2nd millennium BC - The movement of the sun through the sky makes possible a simple estimate of time, from the length and position of a shadow cast by a vertical stick. If marks are made where the sun's shadow falls, the time of day can be recorded in a consistent manner. The result is the sundial. An Egyptian example survives from about 800 BC, but the principle is certainly familiar to astronomers very much earlier. However it is difficult to measure time precisely on a sundial, because the sun's path through the sky changes with the seasons. Early attempts at precision in time-keeping rely on a different principle.
Water clock: from the 2nd millennium BC
The water clock, known from a Greek word as the clepsydra, attempts
to measure time by the amount of water which drips from a tank. This
would be a reliable form of clock if the flow of water could be
perfectly controlled. In practice it cannot. The clepsydra has an
honourable history from perhaps 1400 BC in Egypt, through Greece and
Rome and the Arab civilizations and China, and even up to the 16th
century in Europe. But it is more of a toy than a timepiece.
2 Videos one on Greek mechanical equipment and an interesting clock can be shown here.
Hourglass:
The hourglass, using the flow of sand, has had an even longer career.
It was a standard feature on 18th-century pulpits in Britain,
ensuring sermons of sufficient length! In a reduced form it can still
be found - Particularly as timers in kitchens.
The hour: 14th century AD
Until the arrival of clockwork, in the 14th century AD, the hour was
a variable concept. It was a practical division of the day into 12
segments (12 being the most convenient number for dividing into
fractions, since it is divisible by 2, 3 and 4). (For the same reason
60, divisible by 2, 3, 4, 5, 6, 10, 12, 15, 20 and 30 has been used
ever since Babylonian times.) The traditional concept of the hour, as
one twelfth of the time between dawn and dusk, was useful in terms of
everyday timekeeping. Approximate appointments are easily made, at
times that are easily sensed. Noon was always the sixth hour. Half
way through the afternoon is the ninth hour - famous to Christians as
the time of the death of Jesus on the Cross.
The trouble with the traditional hour was that it differed in length from day to day and a daytime hour was different from one in the night (that was also divided into twelve equal hours).
A mechanical clock could not reflect this variation, but it could offer something more useful - It could provide every day with something that occurs naturally only twice a year at the time of the spring and autumn equinox; a 12 hour day and a 12 hour night. In the 14th century, coinciding with the first practical mechanical clocks, the meaning of an hour gradually changed. It became a specific amount of time, one twenty-fourth of a full solar cycle from dawn to dawn. And the day was now thought of as 24 hours, though it still features on clock faces as two twelve’s.
Minutes and seconds: 14th - 16th century AD
Even the first clocks could measure periods less than an hour, but
soon striking the quarter-hours seemed insufficient. With the arrival
of dials for the faces of clocks, in the 14th century, something like
a minute became necessary and the clocks of the middle ages
inherited, by a tortuous route from Babylon, a scale of scientific
measurement based on 60. In Medieval Latin the unit of one sixtieth
is ‘pars minuta prima’ ('first very small part'), and a
sixtieth of that is ‘pars minute secunda’ ('second very
small part'). Thus, on a principle that was 3000 years old, minutes
and seconds found their way into time.
Minutes are mentioned from the 14th century, but clocks were not precise enough for anyone to bother about seconds until two centuries later. The instrumentation of modern clocks took centuries to evolve to what we see today.
History of Temperature measurement:
Original temperature measurements depended on the Florentine thermometer, because it was developed in the 1650s in Florence's Accademia del Cimento, this pioneering instrument depends on the expansion and contraction of alcohol within a glass tube. This was used for more than half a century.
Mercury thermometer: AD 1714-1742
Gabriel Daniel Fahrenheit, a German glass-blower and instrument-maker
working in Holland, is interested in improving the design of
thermometer. Alcohol expands rapidly with a rise in temperature, but
not at an entirely regular speed of expansion. This makes accurate
readings difficult, as also does the sheer technical problem of
blowing glass tubes with very narrow and entirely consistent bores.
By 1714 Fahrenheit has made great progress on the technical front, creating two separate alcohol thermometers which agreed precisely in their reading of temperature. In that year he hears of the researches of a French physicist, Guillaume Amontons, into the thermal properties of mercury.
Mercury expands less than alcohol (about seven times less for the same rise in temperature), but it does so in a more regular manner. Fahrenheit sees the advantage of this regularity and he has the glass-making skills to accommodate the smaller rate of expansion. He constructs the first mercury thermometer, of a kind which subsequently becomes standard.
There remains the problem of how to calibrate the thermometer to show degrees of temperature. The only practical method is to choose two temperatures which can be independently established, mark them on the thermometer and divide the intervening length of tube into a number of equal degrees. In 1701 Newton has proposed the freezing point of water for the bottom of the scale and the temperature of the human body for the top end. Fahrenheit, accustomed to Holland's cold winters, wanted to include temperatures below the freezing point of water. He therefore acceptet blood temperature for the top of his scale but adopts the freezing point of salt water for the lower extreme. Measurement is conventionally done in multiples of 2, 3 and 4, so Fahrenheit splits his scale into 12 sections, each of them divided into 8 equal parts. This gives him a total of 96 degrees, zero being the freezing point of brine and 96° (in his somewhat inaccurate reading) the average temperature of human blood. With his thermometer calibrated on these two points, Fahrenheit can take a reading for the freezing point (32°) and boiling point (212°) of water.
A more logical Swede, Anders Celsius, proposed in 1742 an early example of decimalization. His Centigrade scale took the freezing and boiling temperatures of water as 0° and 100°. In English-speaking countries this less complicated system took more than two centuries to prevail.
History of Volume:
Among the requirements of traders or tax collectors, a reliable standard of volume is the hardest to achieve. Nature provided some very rough averages, such as goatskins. Baskets, sacks or pottery jars could be made to approximately consistent sizes that were sufficient for many everyday transactions.
But where the exact amount of any commodity needed to be known,
weight was the measure more likely to be relied upon.
More history:
Astronomers, travellers, scientists and traders recognized the need
for more accurate measurements, standards and instruments.
Astronomers needed tools to measure angles at which stars are placed
in the sky.
The land travellers needed to understand elevations of the land better. Also Barometers were discovered to measure atmospheric pressure when they discovered that atmospheric pressure differed with altitude. The travellers also needed to know their coordinates (Latitude and Longitude) and also the time.
Over a period of time the methods have been improvised, measurement units defined and advances in instrumentation abilities have made measurements more accurate and handy.