Mensuration problems
Problem 1
Exercise 16.1
Problem 7.
1)Craft teacher of a school taught the students to prepare cylindrical pen holders out of card board. In a class of strength 42, if each child prepared a pen holder of radius 5 cm and height 14 cm, how much cardboard was consumed?
- Interpretation;
Case 1)Pen stand which is open on top and closed base. Then we have to calculate Curved surface area of cylinder and area of one circle.
- skills
visualising the cylinder into rectangle and circle
- Assumptions:
Concepts used
- basics of circles -radius
- area of circles
- addition and multiplication of fractions
- unit of area
knowledge to be used
- knowledge of Polygons -Rectangles
- knowledge of measurements
- Formula of CSA of cylinder
- substitution
- computing
- Value of Л
Concepts to be taught
- basics of circles -radius
- area of circles
- relation between circumference of circle and length of rectangle in a cylinder
- addition and multiplication of fractions
- unit of area
solution: r=5cm, h=14cm, Л=
Curved surface area of cylinder and area of one circle= CSA of cylinder+area of circle
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2Лrh+Лr^2}
=
=440+78.5
=518.5cm
Cardboard required to prepare 42 penstands= 42X518.5
=
=
Case 2:- Hollow pen stand: Pen stand which is open both the sides i.e., top and base.
Then we have to calculate Curved surface area of cylinder.
Case 3:-Pen stand which is closed both the sides i.e., top and base.
Then we have to calculate total surface area of cylinder.
Activity Making use of 2200 cmcardboard sheet how many hollow cylinders of radius 7 cm and height 5 cm can be prepared.
Problem 2
Solved problems on cone Example 1
- Find the weight of a solid cone whose base is of diameter 14 cm and vertical height 51,
cm, if the material of which it is made weighs 10gm/
- Statement of the problem:What is the weight of a solid cone whose base is of diameter 14 cm and vertical height 51cm, if the material of which it is made weighs 10gm/
- Interpretation;
Calculating the weight of solid cone by calculating its volume. density of a material is given. it is related to volume and weight.
- Assumptions:
Concepts used
- basics of circles -radius
- area of circles
- multiplication of fractions
- unit of volume,density and weight
- density
knowledge to be used
- radius=diameter/2
- density=mass/volume
- knowledge of measurements
- Formula of volume of cones
- substitution
- computing
- Value of Л
Concepts to be taught
- density
- units conversion
solution:
d=14cm r=7cm, h=51cm
Volume of cone=
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{1}{3}{Л}{r^2}h}
=
=
To calculate weight of the solid cone we have to use density of the given material.
density=
=
Weight of solid cone=volumeXdensity
=
=26.18Kg
Problem 3
problem on combination of solids example 01
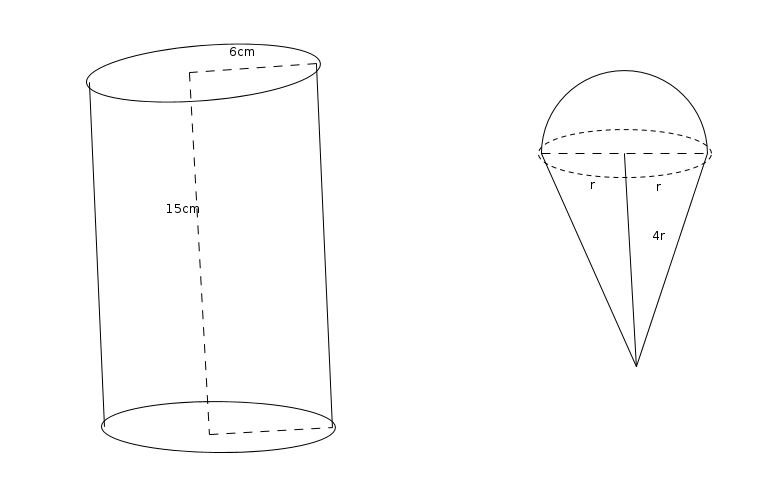
- A Cylindrical container of radius 6cm and height 15cm is filled with ice cream. The whole ice cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height
of the conical portion is 4 times the radius of its base , find the radius of the cream cones.
Solution
Solution
- Statement of the problem
- A Cylindrical container of radius 6cm and height 15cm is filled with ice cream. The whole ice cream has to be filled in 10 equal cones with hemispherical tops. and the height
of the conical portion is 4 times the radius of its base.
.
Assumptions
- Student should know volume of cone,and volume of Hemisphere
- Student should know the value of л=22/7
- Student should know the difference between radius and height
- Student should know the proper substitution simplification
Concepts to be taught
- Let us consider the volume of a cone having hemispherical top =2л
- Volume of Cylindrical container is equated to volume of cone having hemispherical top
Gaps
- Comparision between the volumes of cylinder and (cone+Hemisphere)
Skills
- To imagine a cone , Hemisphere,and cylinder
- To imagine a cone having Hemispherical top
Algorthem
Part 1:
To derive the volume of a cone with hemispherical top
- volume of a cone with hemispherical top
=Failed to parse (syntax error): {\displaystyle {\frac{1}{3}}л{r^2}h+{\frac{2}{3}}л{r^3}}
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {\frac{1}{3}}л4r +{\frac{2}{3}}л{r^3}}
(on simplification)
=Failed to parse (syntax error): {\displaystyle 2л{r^3}}
Part 2 :
To calculate the volume of 10 cone with hemispherical top
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 10X2л{r^3}}
=Failed to parse (syntax error): {\displaystyle 20л{r^3}}
To calculate the volume of ice-cream in cylindrical container
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle л{r^2}h}
= л X6X6X15
=540лc
Part 3 :
To apply condition given in the problem
volume of 10 cone with hemispherical top= volume of cylindrical container
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 20л{r^3}}
=540л
=Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {\frac{540л}{20л}}}
=27
r=3cm
Hence the radius of cream cones=3cm
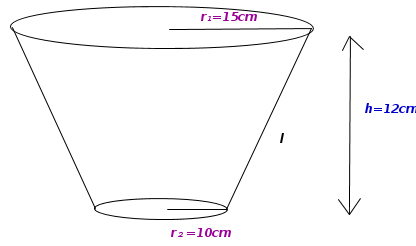
4)Frustum of Cone (Exercise 16.3 Problem 03)
- A bucket in the shape of a frustum with the top and bottom circles of rarii 15cm and 10cm. Its depth is 12cm. Find its curved surface area and total surface area.
(Express the answer in terms of π)