Quadratic equations introduction to quadratic equation actvity 2

From Karnataka Open Educational Resources
Jump to navigation Jump to search

=Activity - CCE ACTIVITY=
Name of Activity Rectangular garden
A gardner wants his garden to have a geometrical shape. He decides on the following rules for building the flowerbeds.

  1. They must all be rectangular
  2. The perimeter and area must be the same.

How many different flower beds can the gardener make if one of the sides ia 3 units less than the other side.

How many different flower beds can the gardener make if both the sides are of same length.

Estimated Time

30min

Materials/ Resources needed

paper and pen

Prerequisites/Instructions, if any

Students need to use their own strategies to solve the equations.
Students may, for example establish a set of equivalent quadratic equations through the balancing method which they are familiar in the context of linear equations.

Multimedia resources

nil
==Website interactives/ links/ simulations/ Geogebra Applets==

Process (How to do the activity)

draw suitable diagram for the problem.
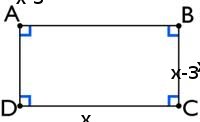
Images.jpeg

Developmental Questions (What discussion questions)

How to find the area and perimeter of the rectangle?
The aim of this activity is to make a situation that leads to the quadratic equation-
x(x-3)=4x-6
Failed to parse (syntax error): {\displaystyle x^2=4x/math><br> Students need to use their own strategies to solve the equations.<br> Students may, for example establish a set of equivalent quadratic equations through the balancing method which they are familiar in the context of linear equations.<br> <math>x^2-3x = 4x-6 => x^2-7x= -6/math><br> <math>x^2-4x = 0/math><br> However ,students will probably have no other methods available but to solve using numerical method. They might set up tables from original eqn.<br> They need to be encouraged to move through the numbers to find the solutions and to make sense of the solution.<br> It also needs to be made explicit here that we are now dealing with an equation that involves a term with an unknown of second degree. This is one feature that distinguishes it from linear equation.<br> #note- In using the balancing method pupil might very well divide both sides of equation<br> <math>x^2 =4x by x}
x=4

Evaluation (Questions for assessment of the child)

  1. how many roots does the linear equation can have?

Question Corner

  1. Can this equation has any other solutions?

Activity Keywords

To link back to the concept page Quadratic_Equations

Retrieved from "https://karnatakaeducation.org.in/KOER/en/index.php?title=Quadratic_equations_introduction_to_quadratic_equation_actvity_2&oldid=32452"