Difference between revisions of "Slope of parallel and perpendicular lines"
Jump to navigation
Jump to search
m (added Category:Co-ordinate Geometry using HotCat) |
|||
| (6 intermediate revisions by one other user not shown) | |||
| Line 16: | Line 16: | ||
==Process (How to do the activity)== | ==Process (How to do the activity)== | ||
Play with the following Geogebra applet <br> | Play with the following Geogebra applet <br> | ||
| − | From | + | |
| − | + | [[http://tube.geogebra.org/material/show/id/143280 From this geogebra applet we can visualise that slope of two parallel lines are same and slope of two perpendicular lise are negetive resiprocals of each other]] | |
==Developmental Questions (What discussion questions)== | ==Developmental Questions (What discussion questions)== | ||
| Line 24: | Line 24: | ||
#Compare the values | #Compare the values | ||
==Evaluation (Questions for assessment of the child)== | ==Evaluation (Questions for assessment of the child)== | ||
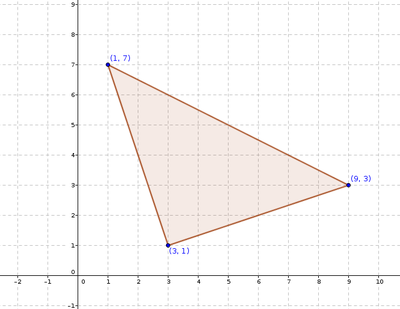
| − | [[Image:evaluation.png]] | + | Can we prove that the given triangle is Right angled triangle?<br> |
| + | [[Image:evaluation .png|400px]] | ||
| + | |||
==Question Corner== | ==Question Corner== | ||
==Activity Keywords== | ==Activity Keywords== | ||
| − | + | ||
| − | [[ | + | [[http://karnatakaeducation.org.in/KOER/en/index.php/Co-ordinate_geometry Back to Co-ordinate geometry Page Link]] |
| + | |||
| + | [[Category:Co-ordinate Geometry]] | ||
Latest revision as of 11:56, 7 November 2019
Activity - Name of Activity
Parallel lines have the same slope and slope of perpendicular lines are the negative reciprocals of each other
Estimated Time
1 Hour
Materials/ Resources needed
Geogebra applet
Prerequisites/Instructions, if any
- Students should know that every line is a representation of an equation /relation between variables
- Graphing an equation/producing equation by visualising graph
- Students should know what is Slope?
- Similarity of two triangles
Multimedia resources
Website interactives/ links/ simulations/ Geogebra Applets
Process (How to do the activity)
Play with the following Geogebra applet
Developmental Questions (What discussion questions)
- Move the Blue points observe the changes
- record the Slopes of two lines
- Compare the values
Evaluation (Questions for assessment of the child)
Can we prove that the given triangle is Right angled triangle?