|
|
| (2 intermediate revisions by 2 users not shown) |
| Line 7: |
Line 7: |
| | #The students have to prove thne angle PAQ=twise the angle OPQ. | | #The students have to prove thne angle PAQ=twise the angle OPQ. |
| | ===Geogebra file=== | | ===Geogebra file=== |
| − | <ggb_applet width="800" height="600" version="4.0" ggbBase64="UEsDBBQACAAIAH2G6UQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZwFSE63siVBORw0KGgoAAAANSUhEUgAAAMgAAABiCAYAAAAV35wWAAATGUlEQVR42u2de1BUV57H+XeqsnErydRkKuvOZmtrk+zWbk1GzfrMZKOJ5rHLxKlkZlNOyozOJCpiFKKggBoEiRIjjooPVHwFBUREheYlojyUh7xfIvLqhobm/eoGab97f+dyu5v3bYRuujnfqlN9H93ndt8+n3vO+f1+5xwHTKLu3r2Lb775BklJSeDisgc5TEWmkZGRDJSCggJ+h7k4ICPpyZMnCAoKgpubG2pra/md5uKAjKTOzk74+flhz549aG1t5XeciwMykurr6+Hh4YHDhw9Dq9XyO2+vBcpheJFatGgRB0SuysvLWbPrwoULvDTZkRwdHYcBotFo2D69ckDMVHp6Ord42blsueawOiCSJItXTk4OL1E2LOpj9vb28j7IVIgsXsHBwdziNQ1FD7Bdu3aNmby8vPDcc89hwYIFI56nPDggkyDqvHOLl22qpaUFer2e1yCWkGTxOnjwILd4cXFARpNk8aLmF5cNFaoBS9ZIJl8OyBQoMzOTdeQTEhJ46bMBxcfHDwNk3rx5bJ9eOSBTpBs3bnCLFxcHZCyZWrwqKyv5PzgNtX//fvY/cUAmWf2t3egpUKFdUYim4DTU7bqOup1RUHlFidt7brLjHUllaM2twn6/77nFy4KSY/Kl9MILL+C9996zC5Ov1QHprW1B499uQeURCZUAQdPZNLTHFKI7swp9qtbBSdmKnuxqtEbloel0KlQCPHnrz2DbyrXY7+PHLV5c9gEI1RT1e2Og3HYF6h/i0C0U+mEwmJE675YjzSUIG+Z/giNfeaJP2zusWcbFNe0B0Wv7oD4Qx8DoKVA+ExSjpdSgq1jz6w/x5cefcTC4bAeQpjOpqN0ciq7U8ikBY2j6u1nP4d9f+Sfcv8pNw1zTGBBtST2q119Eh9DxtgQYlFZ9+0fM+o/nsT9kD5Z8+Bt8tngZczpycU0rQDrii6HcegW91c0Wg6OlQomX5/8C/7biDVSXlmDOzjfhc2Qbli2eg53bPbjFi2t6ANJ46BYaDiVaDAwpfbphJd5ynos3lr/GAMnJScN3lzzwIOkWCv98Ep6u7jzGi8t6gDx9oofSLQKtkbkWh+NxUTHmfTAHUbfD8PJvf4EDV/yQkHodP1zZy87rHjagZtNlFMamwdXVlTkceUeey6KA1LqEWawjPjQtX70MgecCEC9AMed/3kR8ShTWnVyLnlqN4T3U3KtxvoS++nYWskKhKxTCwsU15YCQT6Ptep5V4MjKSMHi/13A4JAAGe29VJNUO/3EajsSBUESKBQUycU1JYC0RReg8cgtq8BB6e3PF+HMpWOyAKHUlfYIKs9rg36DFOPFLV5ckwqItrgOSvcIi8HgsNYB/7L1n9nri84vwOELByxxXGiAQw4glJrOp6M5NGvwbxE679SJp7ghW56NYyJSKBSs2RkREWHYz87ORnh4ONt3d3dHcnIyfHx8xsyH8jh//jxu3ryJ3Nxc5OXlseM05RONGKWRh6mpqdixYweLpbNrQKiZUvWXcxY15Q5Nb30yFz5ndkKREmkWIJSU34az/shQkTmY/jx/f3+7tnip1Wrk5+cjJiYGxcXF7NjevXsZHKWlpWzf19eXvQYEBLBXAmSs4bVRUVHo6enBqlWrGBwpKSnseElJyaD7SwYSgqmsrAw1NTX2CUjD4SR0Jj+0GhyNJVXwdHHDjeRwbD/vCudT6/D18TWY7zhP1ue1JXVQ7Rg9wpRC6qVRjfZm8dLpdEhMTGTbnp6ehuPbt2+Ht7e3YZ8mZSBRrUr9NGnOZQKIpm2iRDWNqegY1SCvvvoqYmNjDbUz3UMav06i2ohAoybtdG3WPhMgFHSodAm1GhyUfLbvRE1O2bDjBI3cPOp9o9H7WDNus8HJycmmZ+gYqujoaMO2BAQV4gMHDmDfvn2sdqH5AY4dO8YKslSDSKIah0YPUsrIyDCWi/5+lndYWBja2toMn6NjlF9ISAjbp7mb7boPQuMzunNqrQYHgUGAjHTOHEB0Ahy1W8Jk/WZ6MpLFiya+s2VRv4Ksd/Q7lEolbt26xZ7odJwgod9JBfzQoUPo6upiTa7AwEBZeR8/fpz1V44ePcpqHGpmxcXFISsri5nUm5qaDH0SuwWE2u1Kj2tWrT0IAmpiPSsglNRCLaItU8v+/TR16kyweK1fvx5FRUXcimWulG5XmD/BWnCU38vD917eY8JjTn5Ui6jcr5pnvROetPQUpCmKqOnAxQExAuIaZtXaY6vTN+h4rJ40QFiTzTlkQveCLDJkvqTEY7w4IOh+UA3NybtWg6MkNRsBPvvHbX6Zm68m8Da6cyc+9SlNm2qvFi8OiBmisePWbF6NV3tMFBBm8v3u2eOypBgve7J4cUDM6n9EWA2OzLg7OHXwqKwO/ETyr90SOmk3lyxBZBqmxU25ZggguvIGNByItxogW77eiJ5qzZQBovK6hifNXZN6ky9dusTC63mM1wwApC2mwGoRu+nRt2TVHs8CSNO5dHSlVUz6jdbqtFi6ZinWbFzDLV72DEjjibvozqqyCiDOf1lnlo9kItdojy5Aa8SDSb/RoZmhuJxxGXuv7sXC/1uIjW4b2QKnXHYGiMpKzsH48Ou4cvrilAPSfe8xNMfvTPqNdg1zhapVxVJ1czW8Q70x13EuvPZ5cYuXXQGyI3La1x7PAgjrh5jpMBxP+qd6uIS6GAAxBcUtyA1vfvgmfgz6cdBn+CBHWwVk+1WLgtHyUImvvvgzq0EsBQhZ6SZTuic6+Mf6DwPEFJSNP2xkoBw+e5gFB3LZKCBKd8sCsupTZ7z04lxW4M1Jv1242OzPSGnLoj/ImqRZbvLw8sCKL1bAxc1lUPrZ/J/B4TcOg9LP/+F1vPKr13nJ5DWI/ESWK/J/2HINcjD+4Kg1CKWj147i+fnPY+PujbxU8j6IeYn8HrbcB+nX94/YB6F0Ku4U5v1uHv7q9leoW9S8RHIr1sQSWbDM6YdM2IqVVYXGI7en1IpF6VL6JSz4wwL8yflPfLZHewKk4ehtqw2SsogfJK4ILaHZk36jT6ecRlxRHC7fv4x3v3oXK79cydeEt0dAWq/nMWeaNQBRXI5E5LnLUwpI88V76LzzcNJvtLZPi6XOS/Hx5x/zNRbtGRBaIs2a81/JrUUmCkjdbqEZ19AxqTeZghUpupeCF7nsHBBm6rViNK9cj/p0iOal4EQKUqThuVwzCBDqqNMQVWvWIuNF9E4EEBrjQtG8zyoKRqRhuDQcl48wnIGAUBu9+af703pMyEQAoUjezpSJh6RT8KE09JZbpmYwIKyZZeUx6eONC7HkmHQKNqQ5nmi4LQ9l54Aw1QqAWHO60ZzENBz3PzRpgNBvUW4NN/s+0LBa6oBLsw1ycUCYaGShem/MtJ3ZxFxAGgIS2XLU3DLFNSmAsM66WwSb6GA6zm5iDiDSojpyRBMwk2WKhtFycUDGFM2uqPKMsmotsn2T64izK5oDCPl1evKV41qmqI9Blik+wIkDIlt1PtFWG4JrOj9vQV4GAq7ug2vwJmw+44Sln74jf15el9Hn5TWdFI5bpjggZkuv7UO1U4hVa5ElnyzEztNuSE5XoCg/k6X5jm/J85zTHF9Cf2okyxQNXOLTinJAnlnkF6m3Yof9+OVD+HztZwY45ALSdiOPBV8OFc1wTv0M0wVf7EqKWiCnCYioFPfd7wPJdYDPA/Fctka4CY/Hz4fyOP8QyGsGKtqB3CZxm3S4EPDLAe4KD5cdGcCeBzMXEFLzuXQ0h1jPebjw9/+FO0mxsgGhiOTazYPDSqSlDezSMqXuAfKFwhtTAxQPNBX3DgRNBgyYqFcLD4ticXEb+MoIqIyqAnqE/ph/HhDySIQjZaC2LRm4RmuvUB3rRZjK2oCazpkJCLNqeV6z2mpTMQlX8eEfl8sChKxWtMqtvlM3yDIlrcVnd9L1A4kqcdvTZCXf7QOL3uzKAjIbAacU4zkvk/eVCoU9SSWm7CELDUnHqoWC/+pPQOxACL+2XwSjRSfWTvqnQHm7mGYqILReIRW8ngKlZRfxFF7LCnLw9qeLEKu4ZgAkP/c+PC5sGz6k1j2C9TskyxT1NezaMhVtsv6fd7axAB/IFwuuVIPsyxVrmvpu4Fix8TNU48QrxZTRaDze/1TMm/K6JtQmbb3GvOg45UM1S5DtNlUdJjtDeirXCJ126pdYuhbJzUrHEsdFyMu9h1+9Oxvu513xutu/4tTNo4aag8bUK2Oy2QKdM8IyRX2JBKFgpzcAyi7glkp8otNxKtjU5wgsMtYGYRXAIaGQd8l4YBwvFvsvBE6WRqyFJLBo/0Y10KQV+yMckME1CTW3WkIyLA7JR6uXY4XH+3hj+WuoLi1BTk4atp7djEfZOXi84QJ+9PTllqnxtP4uUNTC78NUAWLouJ9Ph9pPYVFAaovL8MqSX+LXH/0nA4RScPhhrFg2D1vWOfMJpLmmDyDMBHy3nIVx0KI7loLkg7Xv4+dzXsLl+LP4YPXbeOedd5CcmMT/ba7pBwjrl2j7mJ+EFt6xROxWR2U9Zv39LLz84ksI+e4w/5e5pjcgkljsltBJVu+LnbJQ+ao7uXBasBKzX/olaqtq+D/MZTuASCITq3JbhJCuoDUsC7rKZxu+21vRiIq/xWDrks/h8dEatCkbLPdj3N2B5GTAx8d4jCJ96+rEbYUCyM4m9/zY+dCa4X5+QnWrB1JTgR07gD17jOcpH1OdOCHv+5l6u4dqLI+6dF6OV32sa4z0ntG87mRyTlWb53kf77MKk6mVTpTYBiBD+yh1O6Og8oiE5sQddCSWoKdIaIap24fDUN+GJ40d6HlQg474IjQevY1Hm0Lg67gB7us3W84ypRb+iPx8cTsgQHwlQKhwkzw8xPNUqEtLxWO+vmPnaRrWQqZn8stI0wNpNGKekiorxf0aGTWkqbebfXcZHnUChM6XDpwfz6s+9BrjvWc0rzv77WZ63kf7LLtvWuE+DTg8KztE87WZ3nyrA2IqmlKo7UY+Go8lsyBClgR46ryijPtCagpOQ7uiEME/HmOOvvEsU4WFk2iH1+mAxETj/q5dQKbwJ0gjCqm2iI+nuBXA29v4Pi8v8ZWAoXOUsk0mqKPJHQiKlgHzKtVKEnCkkycHw0RAyrXISd5uuR71gmajQ5F9dxleddN98qEQfOQorOse/p6xvO7st4/geR/tuqN91nDfSowg0baZ3vxpBYhcSTFT6enplr94dLSJ9UFvrEEk/ST88aGhYpNq3z6xtqGaTVrSoLhYBIhSRsbgfOl9IQPj4oOCBucrAUIA3bsnNsG6ZKylaOrtlutRJ5njVTe9hiRySF55PPL3GMvrzn77CE2h0bz5432WoCB47jWIza8u8yImbAoQqy+vTIU+IQEgMJVKsQkVGGg8f+2a+HR/IDRRdu8Wa4mwMKFqPzR+Yc7KElfNaWoy9kni4oxQuLgAzQNtdlq6bcMGoLt7/O8sebu9suR71KWnvVyvuqlHXapBKIqXmjqq7uHvkbzu1MyKqx3sdZf6FXI10mfjBmomAsNF+K+ahdfOPuGepQj3zA4BoTlsqSkVHBxsmzFT69cDRUW2acaZ4V71aQ2I6Wg+PgEbFwfE0F/V4uDBgzxmiosDMlTUjJJjmeLimlGAJAidX+qAZ2Zm8n+FiwMiSbJM3eDrHnNxQIyqrKy0bcsUFwdkKkSWKRrN5+/vzy1TXBwQSZJlitYN12g0/M5zcUBI1HyiZhTNGsItU9ZTzSZ/qHYcgcrrGFouxbJjuscq1PueNrxHc/Iq2m6mQOUZiP72sT3//S3taD5/E+3x90c8b8hLuKaU19DvYM717BIQhULBOuB80crx1dAw+SH6fepm9OSLD6Uap++hq1CiNfI21AcusmPq/edQ+eVutt0edw+a41fYdvPFGLSEJYyZd1tUMjrvPEDp4jXDrkd5NQSIMWVNZ2+gJTxx2Heo+trXrOvZFSCSZUoxdAwDFxwcHFjq6ekxHNPr9WxYsH4getf0HL13Inqq60VHojEY8uH7G9h+07mbeNrbh95KFTqSsvBw2TrRaLJ6F3pr1Gy7bs8ptCvSZAFInxt6PTqmLRYDFeu8g9CRcH/Yd6j8wsvs69k8INSE4papscGQ0qxZsxgQfX19bH/NGvFJ3NbWZjg3e/Zsds7R0ZFtm6O26NRB+2X//dWg/cYjoWi9moTiOavY/qOV37JCrS2tYgVZ3y0aULruF6LpTJQh6R4ZByBpTkRAW1Qx7HqUFzXB2PYnrgyeod9htOvZJSBkmaLON3XCuWXK+qImDT21u9Lz0adsYO380oVfGgoqFebmkFg8aWhG4WsroSuvYceoCVTxmdugwt6ZkovGwHBD0paJiwxR3vn/+BEqfv/t8OsJn2/48SJLXffEkPaRvsNI17MrQEwtU3xpAPsQdaBrtxyw2+tZBBDJMsVjprjsvmls7gcoJMTJyYlbprg4IKaiIEKyTFFQIRcXB2RAppYpLi4OyIAoHIRbprg4IENEMFAgIQUUcssUFwdkQKaWKQpF5+LiAv4f68D+M77/+KgAAAAASUVORK5CYIJQSwcIO9ZP2FcTAABSEwAAUEsDBBQACAAIAH2G6UQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAH2G6UQAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vvdctu4Fb7efQoMZ6fTbSMKIAiQTOXseDO708xk187a7ex0Zy8oEpIQU6SWpGzZsw/QN+htX6Gb5Al6n4fok/QAIClSkn8k24nSqSc2SOIAB/i+cw4OQGbw1WKaoHORFzJLDyxiYwuJNMpimY4PrHk56vnWV88+H4xFNhbDPESjLJ+G5YHlKkkZH1geiZjvh7g3pJz3XM5YLxz5w17kYcJ8l/BgxCyEFoV8mmbfh1NRzMJInEQTMQ1fZlFYasWTspw97fcvLi7sWpWd5eP+eDy0F0VsIRhmWhxY1cVT6K7T6IJqcQdj0v/xu5em+55MizJMI2EhNYW5fPb5Z4MLmcbZBbqQcTmBCVPuW2gi5HgCk/IcYqG+kpoBIjMRlfJcFNC2dasnXU5nlhYLU1X/mblCSTMfC8XyXMYiP7CwTdyAOI6PARGPudQHPLJcirSshGul/bq7wbkUF6ZfdaVVuhYqsywZhqpL9OuvyMEORk9UQUzhQMG5qcLmGaamcEzhmoIZGdc0d42oa2RcI+NSC53LQg4TcWCNwqQADGU6yoG/5r4oLxOhx1M9WE6fPIE5FfIKhCkGQzGgw3OMn6hfDr+uquh3J0laWst8vqXSWiUhzLm7Tuc+OmmtEyBbV+mwa6bJb0DXjOFO82QtaEGV/qd/1zRSZwuN5v5+Crn7QaY46NeuMqi8AxUTJVsxWYppofyFBogFyuwJYuAb3AMrZ4gEUHgOAm9AhCGXwS3xEVelh6gHFS6iyEdKjlCknYP58Mf1dGccMehMPfXAJxEBRS5iFBHtUy4CT0LaL8FHHQoSjCEGjZR64qguKEcuhzvqIxfGqFzSIyBIoSHcg3oHUYKoakw85HDEVX/EVa7OfTV06NJBHCNOVIfg1eDRxptB3kdUzYZXcMl0Ni87EEXTuL4ss1nDBUhDPFqGPROfOlHxs0ESDkUCK8WJYhKh8zBRHqEVjbK0RDWJjnk2zsPZREbFiShLaFWg1+F5+DIsxeJbkC5q3Vo2ytLiOM/K51kyn6YFQlGW4GbMWUJa104zarihrQq3XcFaFbx17W3Um0ENmhcC9Gd5UYuHcfxCSSxDAyB5lCaXX+ciPJtlsjuNQV8vOgMxjxIZyzD9Kxir0qJwQc0apMNVvQYx7tUjyfL45LIAE0aLv4k8gyBDXDto/3gWujRVlDAbt3+A8SIKlfe5QbeRD1WXVR3D3VbE6BbnDUfhQiynO86Vb7duXhRfZ8nykUbgeTgr57lOICA85mpah+k4EdpKtG/D6hydDbPFiTEPavo6vZzBHTYjGI418giig8NgwRxX5dCUWkYNrZHCWgZrCVzbm4ybehI4WkKXQ1NqKTBgM7RqqqSeJsG1GlnomIatynPqeKXMX63181SWL+ubUkZny6mqBt/Pp0PRGFG3T/JQfQ76K1Y2OBN5KpLKqIHMeTYvjI+27D0WkZzCramoIAkVXX+BAZinsRjnoh54opMzA5iuxW1zXXusu/o2z6Yv0vNTsIWVAQz69SgHRZTLmbI5NISF4EwsrSqWRQjrSNxup7wQph6p9QLgKRU04J/zcpLlOv2CsAKlcr5ETCHXQqU2r3Q+FbmMGqBDncfBoObVuLkdmJErlFE2fA3xrlkSTZsljVB9jQGiMJlNQp39VWYWXoq8A43u7bssrhRXckWi0kY0lalOTabhQlsiCocFhMISMmfgIl1mzmZkdSjBWOXl0MTzdYZ+qd0fLkZyIZpADxjJK7CJsDOZpSOUEKXPIBUt9BDKyi/1xZ9lHIu0GW2YgvVoDiBOzcx0EawRwph203QG09cRocV8RcytFA1XKaI23RuKSEUR25ohH9cM+Z8aQzrMN1gfWfflQkf2hg18Rzbw5glumB7ZNL0qZBWKC2y7rqaC2AT2g1dmJ2x2gmquaqHqpDfm6Uq0awMWZdNpmMYo1QnvsQZsmYCFkMo8l3mUiJ+OnqDw5wqeeVlXHpr+ql5uIeBwJwKIY5ZVXe4DCZ5N3W4u8oiMnIixer7CyREgQCr0O3xEN/NRVL3ViEe3MNKa/13i05ZktO3aRBi1qCkMe75NXGc939slsIhfUtOkMImJnM4SGcmywS5RXL9IS0hThF6n17OPMyFmKu07Sk/zMC3U4ZKRaWU11xBo3Gczf8M1/uKb+YNsorXgxLuxp48AGv4IdnZYYfANfLBb+JBjkZ7DaGG/gtACV6d5l7gyg6v6yQIQ6hnLINWjK9LyL3DkXC7QYS1/WEsdwkarF9gU0/ZuAp7TSsWhq3tWsfQQtls97bsbjUVtI+VIRjdzfArZ47qTHhqS4zWShakY3cy1wrahUqxT3U3EP5Sn9hzbD3xCfB/7AC9jVDtuj9nUIR4NCMUudSGr037seDZjxHddx/EYZx6nj+PH16cAHRRH+4LiViD29G7aYTTwvQBquec+PopdA2+i44qJx8aSlUE7jYqWpR9vkx4c75QecBPMVDE0xUPQg4nvcOzzAKwWKDEbFBt7bdJUPvLg6/0tSI+uQ/rVNki/+rBIH41GhSj1Oq+BpOQ+NEC09kiHh2CPePhmGx6+2XOL/zBQ/xBebl45X62hO74Z3Rx6qrEb70lq+4ih/rZE6+MmvtfSerxG6+TutE72hNZHzIP2m9YbN6Tr1MrtNqRyv+klNvNWwuSV3kow3yMeYwy2HOo1yafrtTfSux6QX29H7+s9oXcrdqlNqMccTDCBao8Fnyy5+vXWdZ6rE5r1E6X3/7qZYv3ipCEQpFX71iG4AhV7AacO9wLXDzg3KnY7hyV491PxtfdoWxxO51Ery6nPEpMku/hBjBKx0MDeh4Um49EsHK2z8NtWLPz2fxZ2C3TH1wW6s+0C3dmeBDpmA+kO9TgB3gOi3rZf1udsKt0kNg98SgLmOdz3mH8TO596bFsn9f2brbzqzapXYdsNfO5RSPQwJ36AqffQbuWwO26te66vuQ0e1ev4I8S+49ti39utWHr7EVgid2aJVUcgW7Pk7gdLh9f60rutWHq3zlIAO16X88AlELB8/PAkPcAKtRULbFsWxGKWgxr1erKeo1iUxEJQcWD97pd5Vv7pC/Sfv//z6PjVgblFf0S/fxmeih9/ev/m5y/hrnr8hSnNB3JdJlSfVlfBTotV/b1T9R5JJdG7Lliy0HPoIlN9nFeIXI6abzHNl1jcqleZqoOiDPNSv71Gys0Cm3U+FzMvzWGf5tHOJ2a0fZx1OxPOBiZeHa8z8XZXJpyPmjY8NAsEfI6v0wD7qdX359uQQNdJOD7c4A7vdiWBPoQ77BEN7sr3Cuq9hTncDTreUJ1V3ZkIt0PE6UQW6DjPzkUBATMsK8DvgLf7UY1+BSxu4/Z3B7g61qN2QILu2+RtoGKbbdYxobyxzjuAxR7inT8jH8M6yTWhuoP3EnDXW/0Y+K6IJxXaDvoDgqR9g893k5HkrrnIfVdyvmIGFf8Hzr//ceNqvhbckl1jG/8fXOpdvsF+iO137edaj+23P9HV38JX/7Hr2X8BUEsHCKvWHNNBCgAAdTYAAFBLAQIUABQACAAIAH2G6UQ71k/YVxMAAFITAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV90aHVtYm5haWwucG5nUEsBAhQAFAAIAAgAfYbpRNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAmxMAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAB9hulEq9Yc00EKAAB1NgAADAAAAAAAAAAAAAAAAAD4EwAAZ2VvZ2VicmEueG1sUEsFBgAAAAADAAMAwgAAAHMeAAAAAA==" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" /> | + | <span> </span> |
| | + | |
| | + | <span></span><div id="ggbContainer14a2b70cb23c6cb8374fd4f22e997e08"></div><span></span> |
| | | | |
| | ==Concepts used== | | ==Concepts used== |
| Line 154: |
Line 156: |
| | #OB and OF are the radii of the semicircle with center "O". | | #OB and OF are the radii of the semicircle with center "O". |
| | #PC and PF are the radii of the circle with center "P". | | #PC and PF are the radii of the circle with center "P". |
| | + | |
| | + | ==Ex 4.4.2== |
| | + | #Suppose two chords of a circle are equidistant from the centre of the circle, prove that the chords have equal length. |
| | + | '''DATA''' :- Let AB & CD are the two chords which are equidistant from the centre 'O' of the circle. [ Here OP is the perpendicular distance from the centre O to the chord AB and OQ is the perpendicular distance from the centre O to the chord CD] OP = OQ. |
| | + | |
| | + | '''TO PROVE :-''' AB = CD, |
| | + | |
| | + | '''CONSTRUCTION :-''' Join OA & OD. |
| | + | |
| | + | '''PROOF :-''' |
| | + | {[Consider In ∆AOP & ∆DOQ OA = OD OP = OQ Angle APO = Angle DQO ∆AOP ≡ ∆DOQ AP = DQ Let AB = AP + BP = AP + AP = 2AP AB = 2DQ ---------- 1. and CD = CQ + DQ = DQ + DQ CD = 2DQ --------- 2. From equtn 1 & equtn 2 AB = CD |
| | + | Radii of the circle Equi distances from circle |
| | + | SAS Axiom |
| | + | Acording to properties of SAS axiom. |
| | + | |
| | + | Perpendicular drawn from centre to chord which bisect the chord, i.e. AP = BP. |
| | + | |
| | + | Perpendicular drawn from centre to chord which bisect the chord, i.e. CQ = DQ Acording to AXIOM-1]} |
| | + | |
| | + | angle |
| | + | {| class="wikitable" |
| | + | |- |
| | + | |'''Steps''' |
| | + | |'''Explanation''' |
| | + | |- |
| | + | |[[Image:solution.png|300px|link=http://karnatakaeducation.org.in/KOER/en/index.php/File:Solution.png]] |
| | + | |Explanation for thestep |
| | + | |- angle |
| | + | |Write the step |
| | + | |Explanation for thestep |
| | + | |}|} |
| | + | |
| | + | [[Category:Circles]] |
Latest revision as of 17:12, 29 October 2019
Problem 1
Tangents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠ OPQ
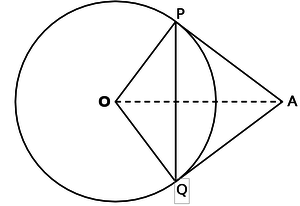
Interpretation of the problem
- O is the centre of the circle and tangents AP and AQ are drawn from an external point A.
- OP and OQ are the radii.
- The students have to prove thne angle PAQ=twise the angle OPQ.
Geogebra file
Concepts used
- The radii of a circle are equal.
- In any circle the radius drawn at the point of contact is perpendicular to the tangent.
- The tangent drawn from an external point to a circle a] are equal b] subtend equal angle at the centre c] are equally inclined to the line joining the centre and extrnal point.
- Properties of isoscles triangle.
- Properties of quadrillateral ( sum of all angles) is 360 degrees
- Sum of three angles of triangle is 180 degrees.
Algorithm
OP=OQ ---- radii of the same circle
OA is joined.
In quadrillateral APOQ ,
∠APO=∠AQO= [radius drawn at the point of contact is perpendicular to the tangent]
[radius drawn at the point of contact is perpendicular to the tangent]
∠PAQ+∠POQ=
Or, ∠PAQ+∠POQ=
∠PAQ =  -∠POQ ----------1
-∠POQ ----------1
Triangle POQ is isoscles. Therefore ∠OPQ=∠OQP
∠POQ+∠OPQ+∠OQP=
Or ∠POQ+2∠OPQ=
2∠OPQ= - ∠POQ ------2
- ∠POQ ------2
From 1 and 2
∠PAQ=2∠OPQ
Problem-2
In the figure two circles touch each other externally at P. AB is a direct common tangent to these circles. Prove that
a). Tangent at P bisects AB at Q
b). ∠APB=90° (Exescise-15.2, B.3)
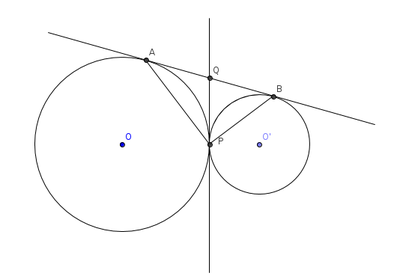
Interpretation of the problem
- In the given figure two circles touch externally.
- AB is the direct common tangent to these circles.
- PQ is the transverse common tangent drawn to these circles at point P.
- Using the tangent properties students have to show AQ=BQ and ∠APB=90°
Concepts used
- The tangent drawn from an external point to a circle
a) are equal
b] subtend equal angle at the center
c] are equally inclined to the line joining the center and external point.
- Angle subtended by equal sides are equal.
- Axiom-1:- "Things which are equal to same thing are equal"
[Click here for geogebra animation]
Algorithm
In the above figure AB is direct common tangent to two circles and PQ is the Transverse common tangent.
a)
AQ=QP and BQ=QP (Tangents drawn from external point are equal)
By axiom-1, AQ=BQ
∴tangent at P bisects AB at Q.
b)
Let ∠QBP=x˚
∴∠QPB=x˚ (∵PQ=BQ)
Now Let ∠PAQ=y˚
∠QPA=y˚ (∵ PQ=AQ)
∴In △PAB
∠PAB+∠PBA+∠APB=180˚
y˚+x˚+(x˚+y˚)=180˚
2x˚+2y˚=180˚
2(x˚+y˚)=180˚
x˚+y˚=90˚
∴ ∠APB=90˚
problem 3 [Ex-15.2 B.7]
Circles  and
and  touch internally at a point A and AB is a chord of the circle
touch internally at a point A and AB is a chord of the circle intersecting
intersecting  at P, Prove that AP= PB.
at P, Prove that AP= PB.
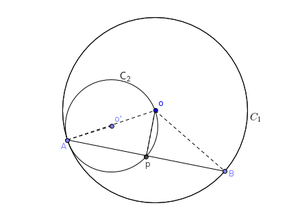
Concepts used
- The radii of a circle are equal
- Properties of isosceles triangle.
- SAS postulate
- Properties of congruent triangles.
Prerequisite knowledge
- The radii of a circle are equal.
- In an isosceles triangle angles opposite to equal sides are equal.
- All the elements of congruent triangles are equal.
Algoritham
In ∆AOB
AO=BO [Radii of a same circle]
∴ ∠OAB = ∠OBA --------------I [∆AOB is an isosceles ∆}
Then,
In ∆AOP and ∆BOP,
AO = BO [Radii of a same circle]
OP=OP [common side]
∠OAP = ∠OBP [ from I]
∴ ∆AOP ≅ ∆BOP [SAS postulate]
∴ AP = BP [corresponding sides of congruent triangles ]
problem-4
In the given Quadrilateral ABCD , BC=38cm , QB=27cm , DC=25cm and AD⊥DC find the radius of the circle.(Ex:15.2. A-6)
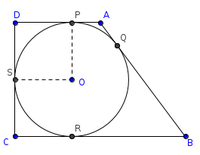
Interpretation of problem
- In the quadrilateral ABCD sides BC , DC & QB are given .
- AD⊥DC.
- Asked to find the radius OS or OP
Concepts used
- Tangents drawn from an external point to a circle are equal.
- In a quadrilateral, if all angles are equal and a pair of adjacent sides are equal then it is a square
- In a circle, the radius drawn at the point of contact is perpendicular to the tangent
Algorithm
In the fig BC=38 cm and BQ=27 cm
BQ=BR=27 cm (∵ by concept 1)
∴CR=BC-BR=38-27=11 cm
CR=SC=11 cm (∵ by concept 1)
DC=25 cm
∴ DS=DC-SC=25-11=14 cm
DS=DP=14 cm (∵ by concept 1)
Also AD⊥DC, OP ⊥ AD and OS ⊥ DC
∠D=∠S=∠P=90˚
⇒ ∠O=90˚
∴ DSOP is a Square
SO=OP=14 cm
hence Radius of given circle is 14 cm
Problem 5 [Ex-15.2-B8]
A circle is touching the side BC of △ABC at P. AB and AC when produced are touching the circle at Q and R respectively. Prove that AQ = [perimeter of △ABC].
[perimeter of △ABC].
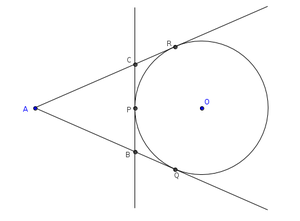
Algorithm
In the figure AQ , AR and BC are tangents to the circle with center O.
BP=BQ and PC=CR (Tangents drawn from external point are equal) ---------- (1)
Perimeter of △ABC=AB+BC+CA
=AB+(BP+PC)+CA
=AB+BQ+CR+CA ------ (From eq-1)
=(AB+BQ)+(CR+CA)
=AQ+AR ----- (From fig)
=AQ+AQ -- --- (∵AQ=AR)
=2AQ
∴ AQ =  [perimeter of △ABC]
[perimeter of △ABC]
Problem-6 [Ex-15.4-B3]
In circle with center O , diameter AB and a chord AD are drawn. Another circle drawn with OA as diameter to cut AD at C. Prove that BD=2OC.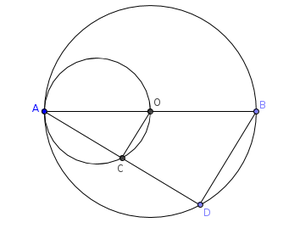
Algorithm
In figure, AB is the diameter of circle  and AO is the diameter of the circle
and AO is the diameter of the circle 
in △ADB and △ACO
∠ADB=90° and ∠ACO=90° [∵angles in the semi circles]
∠DAB=∠CAO [∵common angles]
∴△ADB∼△ACO [∵equiangular triangles are similar]
∴ =
= =
= [∵corresonding sides of a similar triangles are proportional]
[∵corresonding sides of a similar triangles are proportional]
But AB=2OA----1 (∵diameter is twice the radius of a cicle)
 =
=
from (1)
 =
=
∴BD=2OC
Problem-7 [Ex-15.4-A3]
In the figure AB=10cm,AC=6cm and the radius of the smaller circle is xcm. find x.
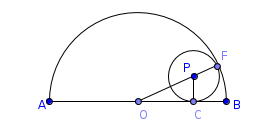
Interpretation of the problem
- In the given figure two circles touch internally.
- OB and OF are the radii of the semicircle with center "O".
- PC and PF are the radii of the circle with center "P".
Ex 4.4.2
- Suppose two chords of a circle are equidistant from the centre of the circle, prove that the chords have equal length.
DATA :- Let AB & CD are the two chords which are equidistant from the centre 'O' of the circle. [ Here OP is the perpendicular distance from the centre O to the chord AB and OQ is the perpendicular distance from the centre O to the chord CD] OP = OQ.
TO PROVE :- AB = CD,
CONSTRUCTION :- Join OA & OD.
PROOF :-
{[Consider In ∆AOP & ∆DOQ OA = OD OP = OQ Angle APO = Angle DQO ∆AOP ≡ ∆DOQ AP = DQ Let AB = AP + BP = AP + AP = 2AP AB = 2DQ ---------- 1. and CD = CQ + DQ = DQ + DQ CD = 2DQ --------- 2. From equtn 1 & equtn 2 AB = CD
Radii of the circle Equi distances from circle
SAS Axiom
Acording to properties of SAS axiom.
Perpendicular drawn from centre to chord which bisect the chord, i.e. AP = BP.
Perpendicular drawn from centre to chord which bisect the chord, i.e. CQ = DQ Acording to AXIOM-1]}
angle
| Steps
|
Explanation
|
|
Explanation for thestep
|
| Write the step
|
Explanation for thestep
|
|}
















