Difference between revisions of "Slope of parallel and perpendicular lines"
Jump to navigation
Jump to search
| Line 24: | Line 24: | ||
#Compare the values | #Compare the values | ||
==Evaluation (Questions for assessment of the child)== | ==Evaluation (Questions for assessment of the child)== | ||
| + | Can we prove that the given triangle is Right angled triangle? | ||
[[Image:evaluation .png]] | [[Image:evaluation .png]] | ||
Revision as of 22:03, 13 August 2014
Activity - Name of Activity
Parallel lines have the same slope and slope of perpendicular lines are the negative reciprocals of each other
Estimated Time
1 Hour
Materials/ Resources needed
Geogebra applet
Prerequisites/Instructions, if any
- Students should know that every line is a representation of an equation /relation between variables
- Graphing an equation/producing equation by visualising graph
- Students should know what is Slope?
- Similarity of two triangles
Multimedia resources
Website interactives/ links/ simulations/ Geogebra Applets
Process (How to do the activity)
Play with the following Geogebra applet
From the following geogebra applet we can visualise that slope of two parallel lines are same and slope of two perpendicular lise are negetive resiprocals of each other
Developmental Questions (What discussion questions)
- Move the Blue points observe the changes
- record the Slopes of two lines
- Compare the values
Evaluation (Questions for assessment of the child)
Can we prove that the given triangle is Right angled triangle?
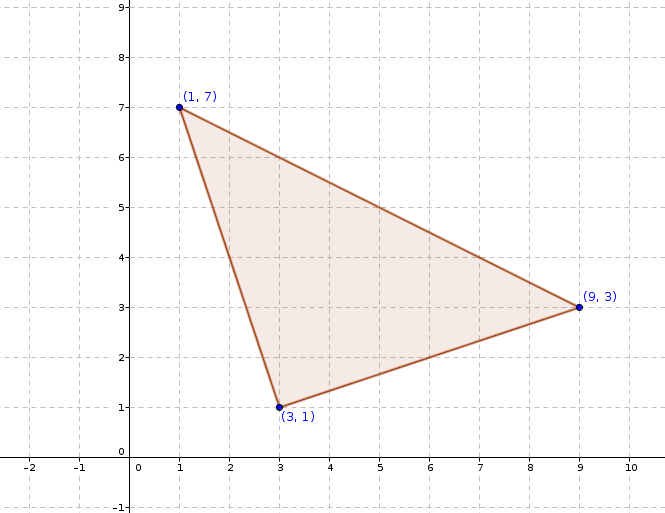
Question Corner
Activity Keywords
To link back to the concept page Topic Page Link