Difference between revisions of "Circles Tangents Problems"
Jump to navigation
Jump to search
| Line 2: | Line 2: | ||
Tangents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠ OPQ | Tangents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠ OPQ | ||
[[File:image_circle_with_tangents.png|300px]] | [[File:image_circle_with_tangents.png|300px]] | ||
| + | ==Interpretation of the problem== | ||
| + | O is the centre of the circle and tangents AP and AQ are drawn from an external point A. OP and OQ are the radii. The students have to prove thne angle PAQ=twise the angle OPQ. | ||
Revision as of 17:46, 9 July 2014
Problem 1
Tangents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠ OPQ
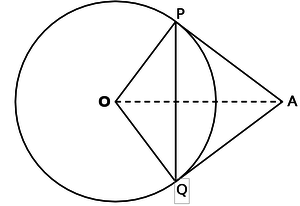
Interpretation of the problem
O is the centre of the circle and tangents AP and AQ are drawn from an external point A. OP and OQ are the radii. The students have to prove thne angle PAQ=twise the angle OPQ.