Difference between revisions of "Circles Tangents Problems"
Jump to navigation
Jump to search
| Line 5: | Line 5: | ||
O is the centre of the circle and tangents AP and AQ are drawn from an external point A. OP and OQ are the radii. The students have to prove thne angle PAQ=twise the angle OPQ. | O is the centre of the circle and tangents AP and AQ are drawn from an external point A. OP and OQ are the radii. The students have to prove thne angle PAQ=twise the angle OPQ. | ||
==Concepts used== | ==Concepts used== | ||
| − | # | + | #The radii of a circle are equal. |
| − | # In any circle the radius drawn at the point of contact is perpendicular to the tangent. | + | #In any circle the radius drawn at the point of contact is perpendicular to the tangent. |
| − | # The tangent drawn from an external point to a circle a] are equal b] subtend equal angle at the centre c] are equally inclined to the line joining the centre and extrnal point. | + | #The tangent drawn from an external point to a circle a] are equal b] subtend equal angle at the centre c] are equally inclined to the line joining the centre and extrnal point. |
| − | # Properties of isoscles triangle. | + | #Properties of isoscles triangle. |
| − | # Properties of quadrillateral ( sum of all angles) is 360 degrees | + | #Properties of quadrillateral ( sum of all angles) is 360 degrees |
| − | # Sum of three angles of triangle is 180 degrees. | + | #Sum of three angles of triangle is 180 degrees. |
| + | ==Algorithm== | ||
| + | OP=OQ ---- radii of the same circle | ||
| + | OA is joined. | ||
| + | In quadrillateral APOQ , | ||
| + | ∠APO=∠AQO= [radius drawn at the point of contact is perpendicular to the tangent] | ||
| + | ∠PAQ+∠POQ= | ||
| + | Or, ∠PAQ+∠POQ= | ||
| + | ∠PAQ = -∠POQ ----------1 | ||
| + | Triangle POQ is isoscles. Therefore ∠OPQ=∠OQP | ||
| + | ∠POQ+∠OPQ+∠OQP= | ||
| + | |||
| + | Or ∠POQ+2∠OPQ= | ||
| + | 2∠OPQ=- ∠POQ ------2 | ||
| + | From 1 and 2 | ||
| + | ∠PAQ=2∠OPQ | ||
Revision as of 17:51, 9 July 2014
Problem 1
Tangents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠ OPQ
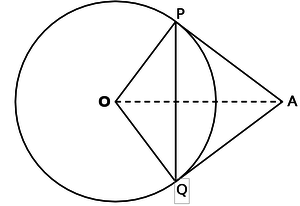
Interpretation of the problem
O is the centre of the circle and tangents AP and AQ are drawn from an external point A. OP and OQ are the radii. The students have to prove thne angle PAQ=twise the angle OPQ.
Concepts used
- The radii of a circle are equal.
- In any circle the radius drawn at the point of contact is perpendicular to the tangent.
- The tangent drawn from an external point to a circle a] are equal b] subtend equal angle at the centre c] are equally inclined to the line joining the centre and extrnal point.
- Properties of isoscles triangle.
- Properties of quadrillateral ( sum of all angles) is 360 degrees
- Sum of three angles of triangle is 180 degrees.
Algorithm
OP=OQ ---- radii of the same circle
OA is joined.
In quadrillateral APOQ , ∠APO=∠AQO= [radius drawn at the point of contact is perpendicular to the tangent]
∠PAQ+∠POQ=
Or, ∠PAQ+∠POQ=
∠PAQ = -∠POQ ----------1
Triangle POQ is isoscles. Therefore ∠OPQ=∠OQP ∠POQ+∠OPQ+∠OQP=
Or ∠POQ+2∠OPQ=
2∠OPQ=- ∠POQ ------2
From 1 and 2
∠PAQ=2∠OPQ