Difference between revisions of "Circles Tangents Problems"
Jump to navigation
Jump to search
| Line 31: | Line 31: | ||
∠PAQ=2∠OPQ | ∠PAQ=2∠OPQ | ||
=Problem-2= | =Problem-2= | ||
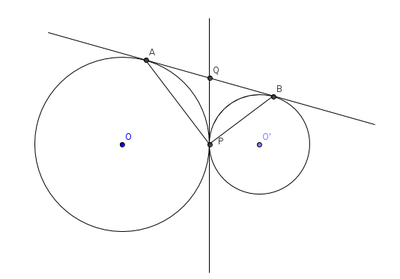
| − | In the figure two circles touch each other externally at P. AB is a direct common tangent to these circles. Prove that<br>a). Tangent at P bisects AB at Q<br> b). ∠APB=90° (Exescise-15.2, B.3) | + | In the figure two circles touch each other externally at P. AB is a direct common tangent to these circles. Prove that<br>a). Tangent at P bisects AB at Q<br> b). ∠APB=90° (Exescise-15.2, B.3)<br> |
[[File:fig2.png|400px]] | [[File:fig2.png|400px]] | ||
Revision as of 09:54, 12 August 2014
Problem 1
Tangents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠ OPQ
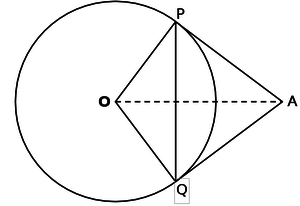
Interpretation of the problem
- O is the centre of the circle and tangents AP and AQ are drawn from an external point A.
- OP and OQ are the radii.
- The students have to prove thne angle PAQ=twise the angle OPQ.
Geogebra file
Concepts used
- The radii of a circle are equal.
- In any circle the radius drawn at the point of contact is perpendicular to the tangent.
- The tangent drawn from an external point to a circle a] are equal b] subtend equal angle at the centre c] are equally inclined to the line joining the centre and extrnal point.
- Properties of isoscles triangle.
- Properties of quadrillateral ( sum of all angles) is 360 degrees
- Sum of three angles of triangle is 180 degrees.
Algorithm
OP=OQ ---- radii of the same circle
OA is joined.
In quadrillateral APOQ ,
∠APO=∠AQO= [radius drawn at the point of contact is perpendicular to the tangent]
∠PAQ+∠POQ=
Or, ∠PAQ+∠POQ=
∠PAQ = -∠POQ ----------1
Triangle POQ is isoscles. Therefore ∠OPQ=∠OQP
∠POQ+∠OPQ+∠OQP=
Or ∠POQ+2∠OPQ=
2∠OPQ=- ∠POQ ------2
From 1 and 2
∠PAQ=2∠OPQ
Problem-2
In the figure two circles touch each other externally at P. AB is a direct common tangent to these circles. Prove that
a). Tangent at P bisects AB at Q
b). ∠APB=90° (Exescise-15.2, B.3)