Difference between revisions of "Slope of a line"
| Line 98: | Line 98: | ||
|} | |} | ||
[[File:Slope of segment.png|250px]]<br> | [[File:Slope of segment.png|250px]]<br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=='''Positive and Negetive Slope'''== | =='''Positive and Negetive Slope'''== | ||
Revision as of 20:15, 13 August 2014
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Textbook
Please click here for Karnataka and other text books.
Additional Information
Useful websites
For more video lessons on Slope click
Reference Books
Teaching Outlines
understanding what is a Slope
Learning objectives
- Slope is measure of the steepness of a line.
- Students will understands that slope increases with the steepness.
- Students will recognize and make a connection between the magnitude of the slope and the steepness of a line.
- Students will understands that Slope is a number (magnitude).
- Students understands that Slope is the orientation or inclination of a line with the X-axis.
- Students should also be able to draw a line with a specific slope.
Notes for teachers
Slope is a number which represents the steepness of a line Students can relate the slope of line to the tangent of the angle of elevation.
Activities
- Activity No #1 'understanding What is a slope?- Activity No1
Procedure
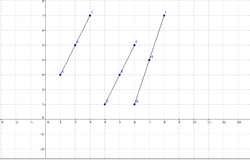
Ask the students to observe the given table describe the pattern using words .
Ask them to plot and join the points on grids and ask how the line segments is visible in the graph.
ask them to write the relation between X and Y.
(we can come to a conclusion that the larger the absolute value of the number,the linebecomes steeper.)
| X | Y |
| 6 | 1 |
| 7 | 2 |
| 8 | 3 |
| 9 | 4 |
| X | Y |
| 4 | 1 |
| 5 | 3 |
| 6 | 5 |
| X | Y |
| 6 | 1 |
| 7 | 4 |
| 8 | 7 |
Positive and Negetive Slope
Learning objectives
- Students should also be able to visualise a line with positive and negetive Slope
- Students should also be able to differentiate a line with positive and negetive Slope
Notes for teachers
If the change in Y with the value of X decreases corresponding line will have Negetive Slope
If the change in Y with the value of X increases corresponding line will have Positive Slope
Activities
- Activity No 1
Observe the following table and analyse the relation between X and Y (X,Y).
You will find that in one case the value of Y goes on incresing with the value of x ,but in the other case the value of Y goes on decreasing with the value of x.
In both the cases visualise the orientation of line segment.
If the value of Y decrease with the value of X the line will have negetive slope
If the value of Y increse with the value of X the line will have negetive slope
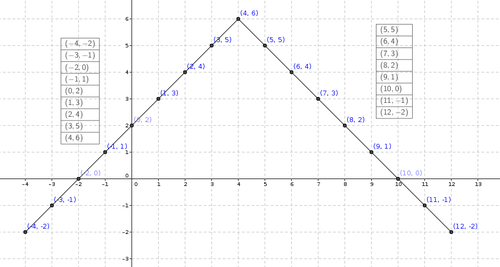
- Activity No 2
The following Geogebra applet helps in visualising Positive and negetive Slope
Slopes of Parallel and perpendicular lines
Play with the following Geogebra applet
From the following geogebra applet we can visualise that slope of two parallel lines are same and slope of two perpendicular lise are negetive resiprocals of each other
Slopes of Parallel and Perpendicular lines