Revision as of 22:29, 13 August 2014

Activity - Name of Activity

Activity 1
Positive and negetive slope

Estimated Time

1 Hour

Materials/ Resources needed

Graph sheets

Prerequisites/Instructions, if any

students should know what is slope/how to calculate if coordinates of the points on the are given
basic operation of numbers

Multimedia resources

Website interactives/ links/ simulations/ Geogebra Applets

Process (How to do the activity)

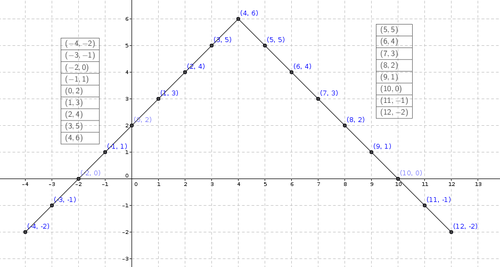
Observe the following table and analyse the relation between X and Y (X,Y).
You will find that in one case the value of Y goes on incresing with the value of x ,but in the other case the value of Y goes on decreasing with the value of x. In both the cases visualise the orientation of line segment. If the value of Y decrease with the value of X the line will have negetive slope If the value of Y increse with the value of X the line will have negetive slope

Developmental Questions (What discussion questions)

Evaluation (Questions for assessment of the child)

Question Corner

Activity Keywords

To link back to the concept page Topic Page Link

The following Geogebra applet helps in visualising Positive and negetive Slope

@@ Line 4: / Line 4: @@
 ==Estimated Time==
+Hour
 ==Materials/ Resources needed==
+Graph sheets
 ==Prerequisites/Instructions, if any==
+#students should know what is slope/how to calculate if coordinates of the points on the are given
+#basic operation of numbers
 ==Multimedia resources==
 ==Website interactives/ links/ simulations/ Geogebra Applets==
 ==Process (How to do the activity)==
+Observe the following table and analyse the relation between X and Y (X,Y).<br>You will find that in one case the value of Y goes on incresing with the value of x ,but in the other case the value of Y goes on decreasing with the value of x.
+In both the cases visualise the orientation of line segment.
+If the value of Y decrease with the value of X the line will have negetive slope
+If the value of Y increse with the value of X the line will have negetive slope<br>
+[[Image:Positive and negetive Slope.png|500px]]
 ==Developmental Questions (What discussion questions)==
 ==Evaluation (Questions for assessment of the child)==
@@ Line 17: / Line 26: @@
 '''To link back to the concept page'''
 [[Topic Page Link]]
-Observe the following table and analyse the relation between X and Y (X,Y).<br>You will find that in one case the value of Y goes on incresing with the value of x ,but in the other case the value of Y goes on decreasing with the value of x.
-In both the cases visualise the orientation of line segment.
-If the value of Y decrease with the value of X the line will have negetive slope
-If the value of Y increse with the value of X the line will have negetive slope<br>
-[[Image:Positive and negetive Slope.png|500px]]
-#Activity No 2 <br>
 The following Geogebra applet helps in visualising Positive and negetive Slope
 <ggb_applet width="1368" height="551" version="4.2" ggbBase64="UEsDBBQACAgIACiC/UQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfdGh1bWJuYWlsLnBuZwFLDbTyiVBORw0KGgoAAAANSUhEUgAAAMgAAABSCAYAAAARpZu7AAANEklEQVR42u1dW3MU1xHen5Eqv1E88MADruIhZYvLC09JoArKXAwkMSKQhEAgckBBGAS2MbFyEVAVMKFIkZRjuRJbETdxSUVGXISEKISEAGt1QzdAt9VqtdpdCdGZ74x6NRrNRUZaaXenp2pq55w+p8+Z3unt/rrnnPX19fWR0xGJRMjtcGrT09ND9fX1Uxoj1eleuEc7ut/vp/v379Pdu3epqqqKhoeHU+oefAMDA46dYrGY65fv1qaurm5K/VOd7oV7ZDoessePH6sTihEIBFL6Hn34hXc6wuGw65fv1sZNQdz6pzo93e8R1uHChQtUXFysFMPOSqTiPfpevHjh2CkUCrl++W5tJihIbIjogVY3/FJdhwKjbt5oOX4diWpnjEJdmhJ/UzlGb2gba/PNPX38yKj2g29Hl94OdO0Y8DeP8eV2TNfGUONXPho/PsZAndY+XFOXcBmlEh3XN27coJKSErp27ZqyEukqA197ezvBzYIlgbIAk6CMT5Q7OzvVNZf52lhGXy7jmvvD/0S5vLx83BixDTkU+ecliu7Mo8j6HBp6+6cU+m+ZKod3/UH1jf7qCEV//jGFtx+hyKr3aWjPURrSPsOo35ij+KH9wO58evbsGQ395o8U+l85hf5xXp3R/M9p+O33qLe4lAJ/K6ThH39Afb29il8QY4G+fCcN/mQ/Da7LpqjG/+WiTAprPDHPyIenVJvo8l9TePNBNR5OzB+nsdzW1mZJZ9mwXIxlK7rV98BlfA9cZl529Nf5Hrm/1feI8u3bt6m0tJQuX75MlZWV4+4B1/gOrPqzTFDmMYzysKObZWzkaaYnUsazj0Fanlv397cQ9QYFg8wSHVYB7hLcJ5xunka64jBfoqNYk8EgEsWafTq7TcARhYWFVFNTI5G8WcMgwAHVft3fBwbp6dVxgxkHjJYVBsC1ERuM4gvwGiy+MYYpGKOAH2Mcxiig4bO2YRwfRed+6MN8Rnmq+RmxkYZ7jHOJYygL/JPM/nVTU5PCEDivXr06LuI03eOnLAaZFQuS9WeixT8j+tFOooOnaOjEv4gKS4j2nyRaukWvHxnRy6uz6eW2I0Qn/k1UfIso7+/69RKt/50axWs4+xjR6f8Qrf0d0ZaP9Tbgt0erzz5OsaKxa1r1W6KLN8fxiZVqD/ymg0SfntV5LPslUeYhoh15ij7ygx1E7+XqcwKf3FP6fYzyGNGwi5oLxsTJ8yu6nlS/jjjLysoUuMYJBREr6mJBxMWyoWvYKB0eDigBlOHKlStKOezaiYIki4LU1I+FePGLrLkjqr/ZdTK4K5HQwJhrZnSTwCsUpghcHEPY2OzeeAmD2FkJwWGpgkH2/UV3neCqrN+nXJ7BkoqJrpPBXXmZsUmvM7tJ2z8l2vABxd7XXLYDn+l08IebdKcmaXzbRI8BJbh06ZJSCDsrke4ySC8MMs2aH/U/9VQUy8pKSCQvQRYEyRHEf5FmhwahEcr4RBkKxACP6eZyf39/vAw+3D8YDKqES0VFxZTGAN3Y3jgGyr29vfEyaE50Y3+cTOc5Md1Y5v5cxmks4x6t6DwflFlGXLaiW8mIy9XV1SrahEQdlAIRJyOdZZSsMkaZx7CSsZlulrFRRmb6dMnYKEOen4D0JP31NFuJJ0+eeE4G3s2DpIFvmgj/myNOVljCKzIQDCIWxNJKIAxrzEuIFU0SCyLrQWb2XSw7KyFrYuRdLE9aELYSsBDm7LVYUcEgnsQgVlYi3XFW2mIQWVE4dTpkaPeOU7rco1dXVfo4hm8XP+fYslMeBDjGKn7e3Nw8qTyI2xgcv7aL0Rtj+FYxersYP8fUOUdgF6Pn/sYYPJQeeQlksPEmLHI+TnkQlpFdjB50pxi9MYZvnJ9bjD9ZZIyyMY9hlQexy3NwmWVklwdJhIwFg1Di34T1AsYQDOJBDMJYAlbC6U1Yr61JFwziUQxiZyVkVxMPYxCv50F4VZ3Tm7CyL5bkQTyFQbChGRQCnzPxJqxgkBTGIOnoYgFWLV6sf+JobGxUGxLghJUw+5riXogMHMO86aYgixa9ovz8BnrzzaDanaOjo0MeDlGQ5MuD4MGcqTwIrAQ2qMMeTleu3Ke33hqmlpZowvIg5vUkbutBJA8ieZAZxSDY/xX4AS7T9evX6d69TqqtRb2+1B2fMBw4QyEIguKneetY8b9FBrYYJJXyINjeknf6w7amvEky6A8eEJ0/T/TVV0Rffkl08SLR8+dEDQ1EBQWDGv4YKxcVjVcSyQGIDOzoSY1BoABQBoBrYAkoiPjfgkFmFINMdx4EWnjgwAGaP38++Xw+mjt3Lm3dutVRe4394TYh/IrcBJQCSiI5AMmDzBZ9WjEIlCAjI4PWrl2rfvlRxkO+YsUKWrBggaWSoA5rJXg7fSsrIf63yCAtMAgsB5TDysXasGEDZWdnx60Ev84Ba9HV1SX+t2CQ9McgcKtgOXB8nneOfrHgMH205q/KihQUFNAbb7xhuV5C/G+RQdJikOnMgwBzIPeB/tsXfURbfJ/RD31ZdObMGfX/EqCny3oQyYN4JA8yXSAdzObMmUMnT55UVuL3W0/R+u/to13f/5NysfBnLADsAlAFpKcUSJ8KBjGvl8jJyZkUBhH/W2SQlhgEVoKjTVbrJTDAwoULlZIAfPNfAq9cuZLmzZtnO0Hxv0UGSYtB3MK8Dx8+HLdDh9Vf/Jp3AEQ0CwrBeZDMzExH7ZUQp8ggacO8ZgxithJ4CXCqvqVsHCcYJKUxCN5rsrMSsi+WYBBPY5Bz585Ra2trQnxL/Lf2ZBRE/G+RQdJikNraWvUA251I/DnR3dqAdvbs2SmNkep0L9xjOsoAASxfe3u7o1a5Rbkm04az66/bP9XpXrjHdJWBax5kZGTEcckq6NhV0A2DsLtldbj1d1syix0cnQ43/sBgbgdWRU7Fv3W6fxx4HcftHtxk6HSfoDnJEXQnOU6Gv5McQXeTIdo4yXEyMnCSI+7fqT/o5nt0zYPIzooS5pUwb4LDdxLmlTBvyoZ53RREdneXKJano1iyN6/kAEQG9nRXBREMIhjE0xgkkftiIcKFyEg6/j+IrAeR9SBiQcSCiAURDCL+t8hAMIj8eooMEpMHEQURBREFEQWRh0NkIBhE/G+RgWAQ+fUUGUynBXHLg3COwCkPwjF2qzzIo0ePXPMgbmPYxdi5zHkIuxi9kW4VowfdKQ9il+fgMsvQKQ/CMrKL0dvlMbjMMrDLgxjpyShjlHkMuzyIkW6VB7HLkyRSxjP+/yDDw6/U/3dUVobVdSz2Kt6/oSEar8fx4MEgdXQMUTA4GK9De9RHIiPqGn1AZ96RyKv4GNwmEAhTbW1EtWU+xrF0Qb1SY6FcURFWdG53+3Zgwvg8d2N/rgMfjF1dPRiv5zkwD2NbjNHUFFJzRp3xuHNngG7exAMxOK6vcXwcLCMjT3wyT/0PjYYm8BcLMgkLMpMYZP/+dsrN7aATJzppyZJvaffuVvr66+eKlpf3PF6PB6OwMKDO/PzWeN2mTc1a+wDt2dNG2dmttHlzM23c6FcPwq5drbRuXSOtX9+oxkCbffvaaMeORrp4sU/xR11FxcC4sUpKuuj06S41VlZWK23b9lTx5TnZjY82S5fq/Q8d0sdbvrxe0cFn8eJvae/eNlq7tpFWr65Tc2AZrF7dEG+LMb744pnqs2pVAxUVBailRX+ztKCgV80zI+ORGv/48RdqDnxv4I367OymCTz5fsATc0QZfZubY4JBvIpB+MF63f5+f1RzF15Oqj+P9V1l5DbH7u7h73wPfn//pMd/Hf4S5rU5pns9iNmNgsl/8iQ0wW1gVwDty8r6JrhdRvciHI4qC4J60HEa3aFgMBJ3x6xcMabDLbJyxYzjW7lish5E/h9k2iyI2Y2CyT98WHcVli2ro8xM3W2Ba8Ltjx1rn+B2GXns3ftUuVRMw4mD3aGsrOa4O4bD7IqBDncF7oiVK2Yc38oVc/v1liiWYJBpy4NYuR+J8C2N47xOf6MrJnkQD2MQWVEoKwq9LIOErwepqqoalwdBNAUhy1AoqtrU1PRSaaleh3IwiLxCWOsTUHU9Pf1qDsAZV692j8bAEaOOqdAo6J2dAcVPbx+iQGBAtQe/8vJuDVd0q/bgW1bWrY0xoNpjTl1dQbp1q1OFSdEH/BsagqqMNuDf3R1QOAXlQKBf1oPI/6QnDoMgHMrhRgBks48P337nzlat/pnCCgiVlpb2KkyQm6vv4bVlS7MC1IxF3n23XmED4JiNG5tUqHPNGj38efToCzU/K76gg+8nn7Sq+ezereMO5gte4PvOO/4JfL3gfwsGSUIMIv63yEAwiPjfIoNUwSCyL5bkAEQG9nRZDyL+t8hgKhhEXCxxsTztYgkGkYdDZOCgIJ2dnQnLg+CAhZJ9sSQPIvtiWRz81wiCQQSDpC0GkTyI5EG8LAPBIOJ/iwycMIjbqyaSB5E8iJdl8H98M/ebWjt8/AAAAABJRU5ErkJgglBLBwge8gLjUA0AAEsNAABQSwMEFAAICAgAKIL9RAAAAAAAAAAAAAAAABYAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzSyvNSy7JzM9TSE9P8s/zzMss0dBUqK4FAFBLBwjWN725GQAAABcAAABQSwMEFAAICAgAKIL9RAAAAAAAAAAAAAAAAAwAAABnZW9nZWJyYS54bWzdWltz27YSfk5/BYZnJk82DRAESSVyOkpO0zqTtJnjnOsbREISaopkCejiTH78WQAkRUq+xIqTZmrZBgkuFthvv10sSY1/3C5ztBa1kmVx7hEfe0gUaZnJYn7urfTsNPF+fPHDeC7KuZjWHM3Kesn1uRf6gbcbB2d+hM1gmcHZNBV0htkpI1l2GjLMTxMawCnOREA5Y4TPPIS2Sj4ryl/5UqiKp+IyXYglf1umXFudC62rZ2dnm83Gb2f3y3p+Np9P/a3KPAQrL9S51xw8A3WDQRtqxQOMydl/3r116k9loTQvUuEhY9VKvvjhyXgji6zcoI3M9AIwoFHioYWQ8wXYGQfEQ2dGqgJjK5FquRYKxvZOrdF6WXlWjBfm+hN3hPLOHg9lci0zUZ972CdhREZJQnGIR5RFMYBZ1lIUuhFuJz1r1Y3XUmycXnPkcMajGJwglZzm4tyb8VyBXbKY1YAprKhewanS17mY8ro93y2InMAHBORHYXSB8xwQ5x6l9ITg0UmM8Qlj2K2lP7GHdFnmVitGbIQ+fUIBDjA6MQ1xTQBNFLlL2PVh6prANaFrmJMJ3fDQiYZOJnQyIb3DzuZ8Z2jTMbC0tZP27SRgn/mL4M8CsGdn0rOTGCM+IWJWbxuKzLqJXb9pwuY0cqexbQh2DWkuJuafxSv6QovoURaR3qyOD7dPesCXdkZCGfv8KYMvMrQzM7jJzIDdYuYXottZynqTwlz21/4dTEkfZOft2H7+jFH4JcF/xIQx/hYTjs/aVDdugg+phZFt+KrFUpm0Q0c28yCCGERmFEOiYIiMoIlNhAaIMBQyOCUJikwbI2qCMkQUJcjIEYpsfmEJ/AttwEaIgS7TGbvIRTREjCJis1KIIBchm9kgywUUJBhDDAaZ2YmZlkYojOCEJiiEBZqcFpu8QWEcnMPkAaIEUTOWxCiIUBSg2ORFEpp0GSVm7aA0QBFGkRkKiRGSokuIMCJB1FgDDK9KJTtwFyKvOq9YHGVRrfQAu3SZtYe63JPOyvTq5R7WgivdHoMQ7Ea7Tc/tToM98ck451ORQ+lwaWiA0JrnJoKt/llZaNRSIHB985pXC5mqS6E1jFLod77mb7kW29cgrdoF2qntXj0WqzSXmeTFv4AjRoVRiHZbt0lM7dbNomaatCzr7PJaAXPQ9n+iLkEyxn446v1ALF27SxQnPpyplBuaM+bj/g8gfd275CYQ684CvhWqhWxey6x/fKFelnnWwV6VstCveKVXta22INXVZuWTYp4Li6Dtg7olvZqW28sm9zpdH64rOGvmn85flXlZIwi7wCAwb9qpa62MWVgnha0MthK49YXMuutkFFgJ205da6XAuW5pjaGktZLgdhqpbLIA5X0qWWaYImhVSP22PdEyvWosJU7+19VyCqRqhg1VkkdSOT7bo9H4StSFyB1XCnDkqlwpx96OgU/GKyXec72YFNk/xBzC7j03mU+Daie6W3EmUrmEga6/gY4bt/4Tlup6MzGvRWthbstbB6y9ivvMPei2ql7X5fKiWH8AzhwsFWrcGngEizD5Ybi88Vlr7ViltawMb9EUEvWV2HEzk4pDms/6IQjQKFCSWpVaagOxh/hKL8ralrcQuNCaKM3FEmpZpC1JLc87d01slWz8gsrp75A7dvuvE9jBCNdvZKzlNs+rBTeldINJzq9FPUDJ6ntXZvvYtahAPqgcSSohHL3cguGgAnU2KHugWmcotIUFmDud66b96G6b3D2CMdUE6iD1ud49LwIJHUr34PXyL4BX2OAVPhJeablc8iJDha083kJO8nYbHseGZIgTg53DZaXbC9ypahQcQG/SWwcsvw/5nq23QY+PB34H3+k+33a6unSsYR+9gltFZQtu3ewO9uAXmWXCFglus/qjcEOUy5JyWeUylfpukC8Kk+gAhD2kuUN6O4EkfYD2q7vRHhL91XFENzfrc9dMXfMIgOMGcHfw0SH/tSL873+BCKc+TSxixDel1FfOiT99Z4hh/xjMiB9byLAfRSTpfUZfHcDX3xmAx1Eubhj3zeH75TuD7zj+hQAc7X1cAFOfkEH3V0fzXbkWHxai28YHuA5K/ceF9bfZTAlt8z0lrj4hXx916kd4tPuQdmMfcvhO0JObQWcPAf3iO6PwMVBGfjiAMmywTIZYPs5+dG/N2aexrYkuDuqh6QOqz+k9sfDNik/sJ4MnIJi2MA96HcpQqiYJ66EfR9+6Un1veT70zfTAFW8eUpq+Oc4XBAc9bxBGv2HG34XvwJUkCVkYRIySmIUj1tQfozgeBUESJ5RQ6A3uDJjRUQFzmZfVfsQcemV5t1eK1VLUMu1wX1qFMP2qXYQfJCwmYfc/bJ6HPDTPWWcBjIwcRBL5TM+RY4k/SOHbqoYRxvHtesVWw6Lgwrn39I9VqZ9vFqJAoF0gMxdSOS+0Qqtqw+sM6dJesQ8W7ZEyjkBpqcyrSJGh5inyWpz4CNIXWpa16PqQVCfo6d8Ifm6HaiEqMLqbaiPz3M1303S+HThRtsc5qZyhLZJFWguuBPpv0wv+KLteZ5PFYeh8Y7g3ROGzozIti0y68AHx3xrpJXo6188RvmebM6nt2Li1T70VkHa2ewkEkfTOhFfYvhFhXpvhSO/xnc1jyMQt3tvnsItbyLVBGAe9D+sH7v00CgY0+veNNMrKTXEXkaRChZhzSxYI2RPEVe/qVEAoC+VIZZKBpYQ9a0ed3EinbtqWc2Zwx7/bSLZtCNUx7LrpyMRDyRU8Arnym8llcsoutXxRFfVY9BoU/KHb4E/pPr0exi46YFdDCEBgXvPMfNPBJAPuHA8k4qiwj+nBj1xbn4LTzPPpKdBnWuqFdXAma+GePxs+dDnJJFWjrmWS73hmKrIdu8yIn7YVOOEBNKDH7fztWxiXQYyn/2QP04Ej6ah5HDtKenkF354/hnv5K1mn+f5m/sYVvdhnB7t6eveuDvHT29PTP7XuvXG3Nu/c7qxT5VwUa1hqWSvAGzffo7rGbgHoY9uzJd2zRdJ0fSS9SgtKvFpu0aSVn7RSk8CoikNME7jNieIYCu4A0veENlNMQlua7Fd3E2YnPKjvbiyvzZtcOZPpw8vr9MDlPz+kvP75uHtRErggs+33cD9qvtYVRCMKaEchTkbM1P+2wGajUZJgQikNIvMVoUe5Iz3rv5Czr8ibr8m9+D9QSwcIE/nSilQJAADWJwAAUEsBAhQAFAAICAgAKIL9RB7yAuNQDQAASw0AABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX3RodW1ibmFpbC5wbmdQSwECFAAUAAgICAAogv1E1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAACUDQAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIACiC/UQT+dKKVAkAANYnAAAMAAAAAAAAAAAAAAAAAPENAABnZW9nZWJyYS54bWxQSwUGAAAAAAMAAwDCAAAAfxcAAAAA" enableRightClick="false" showAlgebraInput="false" enableShiftDragZoom="true" showMenuBar="false" showToolBar="false" showToolBarHelp="true" enableLabelDrags="false" showResetIcon="true" />

Difference between revisions of "Positive and negetive slope"