Slope of a line

The Story of Mathematics

Philosophy of Mathematics

Teaching of Mathematics

Curriculum and Syllabus

Topics in School Mathematics

Textbooks

Question Bank

While creating a resource page, please click here for a resource creation checklist.

Textbook

Please click here for Karnataka and other text books.

Teaching Outlines

Concept 1

understanding what is a Slope

Learning objectives

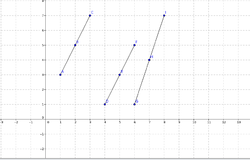
1. Slope is measure of the steepness of a line.
2. Students will understands that slope increases with the steepness.
3. Students will recognize and make a connection between the magnitude of the slope and the steepness of a line.
4. Students will understands that Slope is a number (magnitude).
5. Students understands that Slope is the orientation or inclination of a line with the X-axis.
6. Students should also be able to draw a line with a specific slope.

Notes for teachers

Slope is a number which represents the steepness of a line Students can relate the slope of line to the tangent of the angle of elevation.

Activities

1. Activity No1
   understanding What is a slope?

Procedure
Ask the students to observe the given table describe the pattern using words .
Ask them to plot and join the points on grids and ask how the line segments is visible in the graph.
ask them to write the relation between X and Y.
(we can come to a conclusion that the larger the absolute value of the number,the linebecomes steeper.)

X	Y
6	1
7	2
8	3
9	4

X	Y
4	1
5	3
6	5

X	Y
6	1
7	4
8	7

Assessment Questions

1. Write the relation between X and Y(as an equation)
2. plot the other points following the same pattern and join the points
3. How do we differentiate these lines from one another?from the inclination with the x-axis i.e bending of line towards x-axis
4. Can we visualise the angle so formed by the line with the X-axis?
5. What is the relation between the bending of line and angle formed by it with the X-axis?
   

We can conclude that bending(orientation of line)increases with the increse in the angle or we can say line becomes steeper with the angle of inclination.
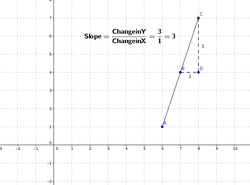
The slope of a line is a number that measures its "steepness" It is the change in y for a unit change in x along the line.

1. How do we measure the steepness of line?

1. Ask the students to measure Slope of other lines
2. Ask the students to inspect the Slope with the help of relation between X and Y
3. What is the slope of a horizontal and a Vertical line?
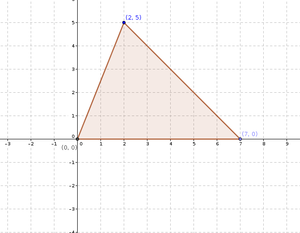
4. Find the slope of three segments of the triangle given below.

Concept 2

Positive and Negetive Slope

Learning objectives

1. Students should also be able to visualise a line with positive and negetive Slope
2. Students should also be able to differentiate a line with positive and negetive Slope

Notes for teachers

If the change in Y with the value of X decreases corresponding line will have Negetive Slope If the change in Y with the value of X increases corresponding line will have Positive Slope

Activities

1. Activity No 1
   

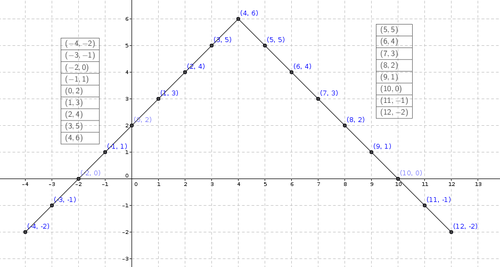
Observe the following table and analyse the relation between X and Y (X,Y).
You will find that in one case the value of Y goes on incresing with the value of x ,but in the other case the value of Y goes on decreasing with the value of x. In both the cases visualise the orientation of line segment. If the value of Y decrease with the value of X the line will have negetive slope If the value of Y increse with the value of X the line will have negetive slope

1. Activity No 2
   

The following Geogebra applet helps in visualising Positive and negetive Slope

Geogebra Applet

==Concept 3==
Slopes of parallel and Perpendicular lines From the following geogebra applet we can visualise that slope of two parallel lines are same and slope of two perpendicular lise are negetive resiprocals of each other Slopes of Parallel and Perpendicular lines