Circles

From Karnataka Open Educational Resources
Revision as of 19:17, 17 May 2017 by KOER admin (talk | contribs) (Text replacement - "<mm>[[" to "[[File:")
Jump to navigation Jump to search
ಕನ್ನಡದಲ್ಲಿ ನೋಡಿ

The Story of Mathematics

Philosophy of Mathematics

Teaching of Mathematics

Curriculum and Syllabus

Topics in School Mathematics

Textbooks

Question Bank

While creating a resource page, please click here for a resource creation checklist.

Concept Map

[maximize]

</mm>

Textbook

ncert books

Class 9 Mathematics contain simple description and theorems on circle

Additional Information

Useful websites

  1. maths is fun A good website on definitions for circles.
  2. Cool math For clear and easy definitions.
  3. Open reference Contains good simulations.
  4. Wikipedia Has good explanations on circles.
  5. Khan academy Has good educative videos.
  6. Arvind gupta toys Contains good information.
  7. nrich.maths.org Refer for understanding Pi.

Reference Books

  1. School Geometry By Hall and Stevens. Part3 pageno 143. Contains basic definitions and proofs given by Euclid.

Teaching Outlines

Introduction to circle

Concept #1 Introduction to Circle

Notes for teachers

Source: http://circlesonly.wordpress.com/tag/inventions/
Summary : The circle is the most primitive and rudimentary of all human inventions, and at the same time, the most dynamic. It is the cornerstone in the foundation of science and technology. It is the basic tool of all engineers and designers. It is used by the greatest artists and architects in the history of mankind. Without a circular shape the wheel, pulleys, gears, ball bearings and a thousand other items we take for granted wouldn’t exist. And of course we would never have the pleasure of driving a car, riding a giant wheel, or watching the moon landing on our television set.
If you look through any old patent claim, you will most likely find the repeated use of circles, spheres, curves, arches, etc. circles are everything and they are nothing. They don’t exist in reality and yet they are the basis of all that mankind has brought into existence. That is why a circle is so fantastic.

Learning objectives

  1. Appreciation of circle as an important shape as it is an intrical component in the invention of almost everything that we see around us.
  2. To make students know that circle is a 2-dimensional plane circular figure.
  3. All points on its edge are equidistant from the center.
  4. The method of drawing a circle
  5. The size of the circle is defined by its radius.
  6. To elicit the difference between a bangle or a circular ring and circle as such.


Circle.jpeg

Activity No # 1. A discussion on “Life without circular shaped figures.”

  • Estimated Time: 45 minutes
  • Materials/ Resources needed: Paper, pen
  • Prerequisites/Instructions, if any:

Previous day homework :

  1. Ask the children to make a list of all circular objects that they can think of :
  2. List as many devices as you can think of that depend on the wheel.(Consider objects in your home, at school, games and toys, machines, vehicles and engines as you make your list.)
  3. Now imagine living in a world without any kind of wheels or rolling devices. How would life be different? Would it be harder? How and why? Describe what it would be like to live without any wheels.
  • Multimedia resources
  • Website interactives/ links/ / Geogebra Applets
  • Process:(How to do the activity)

Have an open discussion with children. Initially let the children share their ideas and do most of the talking. Ensure that the intended discussion remains within the context. Make a mind map on blackboard of all relavant points discussed . Let them appreciate the significance of circular shape thus setting the stage for further study of this fantastic shape called “circles”.

  • Developmental Questions :(What discussion questions)
  1. What all shapes do we see around us ?
  2. Can you imagine bicycles and your other vehicles without circular wheels ?
  3. How different life would have been if wheel was not disovered ?
  4. What about potter's wheel and stone mill?
  5. Do you think that it is necessary for us to study and understand the parameters of circle in depth and detail ?
  • Evaluation:
  1. Do you all now agree that wheel is one of the greatest inventions of mankind? Justify
  • Question Corner:
  1. Are shapes important ? How?
  2. Is bangle a circle ?
  3. When you say shape, what do you mean ?

Activity No # 2. Geogebra animation to explain PI

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ / Geogebra Applets
  1. Click here for Finding Pi by Archimedes Method. Archimedes approximated the value of Pi by starting with the fact that a regular hexagon inscribed in a unit circle has a perimeter of 6. He then found a method for finding the perimeter of a polygon with twice as many sides. Applying his method repeatedly, he found the perimeter of a 12, 24, 48, and 96 sided polygon. Using the perimeter as an approximation for the circumference of a circle he was able to derive an approximation for Pi equivalent to 3.14. This video uses a somewhat simpler method of doing the same thing and carries it out to polygons with millions of sides. All that is needed to understand the calculation is knowledge of the Pythagorean Theorem.
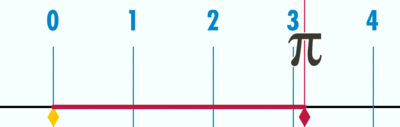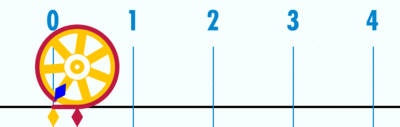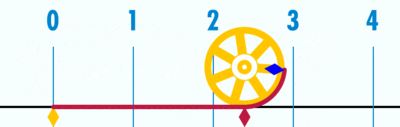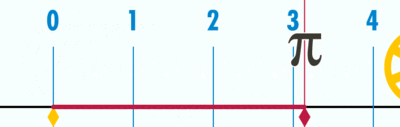
  2. Geogebra file for explaining how 'circumference / diameter' is a constant, denoted as pi (Greek letter), using a number line
  3. An animation of the same concept.

Pi 121.gif

  • Process/ Developmental Questions

Open the Geogebra file. Move the slider to 'unravel' the circumference' over the number line. Since the diameter is 1 unit (measuring from -0.5 to 0.5 on number line), the circumference ends at 3.14, showing the ratio between circumference

  • Evaluation
  • Question Corner

if the diameter is increased from 1 to 2, what will the circumference be?

Activity No # 3. Circle of varying radius using Geogebra

  • Estimated Time: 20 mins
  • Materials/ Resources needed: Laptop, geogebra,projector and a pointer
  • Prerequisites/Instructions, if any:
  1. Theory on circles introduction should have been done.
  • Multimedia resources: Laptop
  • Website interactives/ links/ / Geogebra Applets:

This geogebra file has been made by ITfC-Edu-Team.


  • Process:

Show the geogebra file and ask the following questions.

  • Developmental Questions:
  1. What is a circle ?
  2. Which point is the centre of the circle ?
  3. What is the radius of this circle ?
  4. How do you name the radius ?
  • Evaluation:
  1. By what parameter is the size of a circle defined ?
  2. Bigger the radius, _____________
  • Question Corner:
  1. How do you name a circle ?
  2. Can you draw a circle without knowing the radius ?

Activity No # 3. Is circle a Polygon ? - A debate.

  • Estimated Time: 40 minutes
  • Materials/ Resources needed

Laptop, geogebra file, projector and a pointer.

  • Prerequisites/Instructions, if any
  1. Ensure that lesson on polygons is done.
  • Multimedia resources:Laptop
  • Website interactives/ links/ / Geogebra Applets: This geogebra file has been created by maths STF teachers.

  • Process:

Demonstrate the geogebra file and ask the questions listed below.

  • Developmental Questions:
  1. How many sides does this figure have ?
  2. Name the figure formed.
  3. What is hapenning to the length of the sides as the number of sides is increased ?
  4. What shape is this ?
  5. So, can circle be considered a polygon ? Justify
  • Evaluation:
  1. Are the students able to comprehend that the number of sides is getting infinite as the shape resembles a circle ?
  2. Are the students able to appreciate the application of polygon anology to circles.
  • Question Corner;

Debate between two groups with these two perspectives.

  1. Circle seems to have derived from polygons . Circle can be considered a polygon.

Vs

  1. A polygon is defined by a certain number of sides having non zero length. Then how can circle be a polygon ? (hint: all radii in a circle should be equal ???)

Hints for difficult problems

Problem-1

  1. Tanjents AP and AQ are drawn to circle with centre O, from an external point A. Prove that ∠PAQ=2.∠OPQ

[Solution]

Ex 4.4.2

  1. Suppose two chords of a circle are equidistant from the centre of the circle, prove that the chords have equal length.

DATA :- Let AB & CD are the two chords which are equidistant from the centre 'O' of the circle. [ Here OP is the perpendicular distance from the centre O to the chord AB and OQ is the perpendicular distance from the centre O to the chord CD] OP = OQ.

TO PROVE :- AB = CD,

CONSTRUCTION :- Join OA & OD.

PROOF :- 

    {[Consider  In ∆AOP & ∆DOQ 
                             OA = OD
                              OP = OQ
                 Angle APO = Angle DQO
                        ∆AOP ≡ ∆DOQ 
                            AP = DQ
    Let  AB = AP + BP
                 = AP + AP
                 = 2AP
           AB = 2DQ ---------- 1.
   and  CD = CQ + DQ
                 = DQ + DQ
           CD = 2DQ --------- 2.
  From equtn 1 & equtn 2
            AB = CD

Radii of the circle Equi distances from circle 

SAS Axiom

Acording to properties of SAS axiom.

Perpendicular drawn from centre to chord which bisect the chord, i.e. AP = BP.


Perpendicular drawn from centre to chord which bisect the chord, i.e. CQ = DQ Acording to AXIOM-1]}

angle

Steps Explanation
Solution.png Explanation for thestep
Write the step Explanation for thestep

|}

Project Ideas

Math Fun

Retrieved from "https://karnatakaeducation.org.in/KOER/en/index.php?title=Circles&oldid=27204"