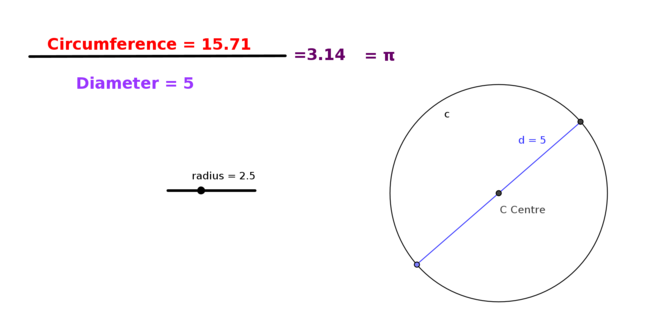Circles
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Introduction
The following is a background literature for teachers. It summarises the things to be known to a teacher to teach this topic more effectively . This literature is meant to be a ready reference for the teacher to develop the concepts, inculcate necessary skills, and impart knowledge in Geometry - Circles from Class 6 to Class 10.
The first step is to understand how to define circles and related terms using geometric vocabulary. The next step is to understand what is Pi. That it is a constant and that for any circle the ratio of the circumference by the diameter is always a constant value Pi. The interesting properties of Pi – an irrational number can also be discussed here in the basic form. Ability for the child to do simple area and perimeter calculations. Next the learner should understand that the circle is a 2 dimensional plane figure and how to visualise solid 3-dimensional figures. What are the solid shapes that have a circle as a part of them. Mensuration – more complex area measurements which include circular shapes. Surface Area and Volume measurement of sold shapes such as cylinder, sphere and cone. Understand the properties of the circles by proving theorems deductively. Also acquire the skills of deductive proofs, understand that all the properties can be deduced from the axioms. Understand the relationship between lines and circles – secant and tangent
Additional Resources[edit | edit source]
Resource Title
OER[edit | edit source]
- Web resources :
- Cool math For clear and easy definitions.
- Wikipedia Has good explanations on circles.
- Khan academy Has good educative videos.
- Arvind gupta toys Contains good information.
- Books and journals
- School Geometry By Hall and Stevens. Part3 pageno 143. Contains basic definitions and proofs given by Euclid.
- Textbooks:
- Class 9 Mathematics contain simple description and theorems on circle
- CLASS 10
- Syllabus documents
Non-OER[edit | edit source]
- Web resources
- maths is funHere you get description of terms of circles
- Intersting facts this web link is full of circle facts.
- sparknotes Gives some more details about properties of circles
- www.regentsprep.com conatins good objective problems on chords and secants
- www.mathwarehouse.com contains good content on circles for different classes
- staff.argyll contains good simulations
- Open reference Contains good simulations.
- nrich.maths.org Refer for understanding Pi.
- This is a video showing construction of tangent at any point on a circle
This is a resource file created by Suchetha, Mathematics teacher, GJC Thyamangondlu
- This is a video showing construction of tangent from external point and theorem
This is a resource file created by Suchetha, Mathematics teacher, GJC Thyamangondl
- This is a video showing Transverse common tangent
This is a resource file created by Gireesh KS , Assistant Teacher, GHS jalige, Bangalore Rural District
- you want see the kannada videos on theorems and construction of circle click here this is shared by Yakub koyyur GHS Nada.
- Books and journals
- Textbooks
- Syllabus documents (CBSE, ICSE, IGCSE etc)
Learning Objectives
- Appreciation of circle as an important shape as it is an intrical component in the invention of almost everything that we see around us.
- To make students know that circle is a 2-dimensional plane circular figure.
- All points on its edge are equidistant from the center.
- The method of drawing a circle
- The size of the circle is defined by its radius.
- To elicit the difference between a bangle or a circular ring and circle as such.
Teaching Outlines
Concept #1 Introduction to Circle
When I tell people that circles are the mother of all inventions, the first thing they ask is, “circles are inventions?”
Yes, a circle isn’t something that exists in nature. It isn’t something that people discovered like gold or the new lands of America. It is a mental construct, a symbolic representation that was invented much the same as language and the alphabet.
There is no way to be certain, but anthropologists generally agree that the circle was created long before recorded history. It is quite likely that it was drawn by a stick in the sand. With the sun being a constant in early man’s existence and the source of all life, it is quite likely that the first circle represented the sun.
Through the years man’s understanding of the circle has evolved substantially with Euclidean geometry being its crowning point of technological understanding. (Having said that, I assure you this blog is not going to be about mathematics or boring scientific equations.)
What we will say that is without the rudimentary understanding of circles, the world would not be anything like it is today. Without circles, there would be no wheel, which is man’s crowning achievement dating back to the Neolithic Age (circa 9500 BC).
The three other great achievements are the ability to make fire, the agriculture of crops, and the domestication of animals. While the circle didn’t have any direct bearing on these advancements, the understanding of circles certainly contributed to their proliferation and expansion.
Besides the wheel, pulleys, gears, ball bearings and a thousand other items we take for granted wouldn’t exist. And of course we would never have the pleasure of driving a car, riding a Ferris wheel, or watching the moon landing on our television set.
If you look through any old patent claim, you will most likely find the repeated use of circles, spheres, curves, arches, etc. They are an intrinsic component in the invention of almost everything that we see around us.
I had a microbiologist challenge me that his field didn’t have much use for circles. Not knowing anything about microbiology, I asked him what was the shape of the lens in his microscope.
The circle is the most primitive and rudimentary of all human inventions, and at the same time, the most dynamic. It is the cornerstone in the foundation of science and technology. It is the basic tool of all engineers and designers. It is used by the greatest artists and architects in the history of mankind.
And it doesn’t exist except in our mental construct. It is a symbol, not a thing. We talk about it in every language on earth. It is written about in millions of textbooks and all over the Internet, and yet we cannot put it in a wheel barrel. It doesn’t exist in a three dimensional world or even a two dimensional world. It is merely a representation.
Immanuel Kant’s famous phrase “ding an sich” applies to the circle. A circle is not a “thing-in-itself.” It is a semantic fabrication that exists only in our imagination. As Alfred Korzybski, the father of General Semantics, would say, it is “the map, not the territory.”
But here we are getting off on a philosophical tangent that might be subject to a future blog entry. For now let’s just say that circles are everything and they are nothing. They don’t exist in reality and yet they are the basis of all that mankind has brought into existence. That is why I think the circle is so fantastic.
Source: http://circlesonly.wordpress.com/tag/inventions/
Summary :
The circle is the most primitive and rudimentary of all human inventions, and at the same time, the most dynamic. It is the cornerstone in the foundation of science and technology. It is the basic tool of all engineers and designers. It is used by the greatest artists and architects in the history of mankind. Without a circular shape the wheel, pulleys, gears, ball bearings and a thousand other items we take for granted wouldn’t exist. And of course we would never have the pleasure of driving a car, riding a giant wheel, or watching the moon landing on our television set.
If you look through any old patent claim, you will most likely find the repeated use of circles, spheres, curves, arches, etc. circles are everything and they are nothing. They don’t exist in reality and yet they are the basis of all that mankind has brought into existence. That is why a circle is so fantastic.
Circle Properties
- A circle is the collection of all points in a plane, which are equidistant from a fixed point in the plane.
- Equal chords of a circle (or of congruent circles)subtend equal angles at the centre.
- If the angles subtended by two chords of a circle(or of congruent circles) at the centre(corresponding centres) are equal, the chords are equal.
- The perpendicular from the centre of a circle to a chord bisects the chord.
- The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
- There is one and only one circle passing through three non-collinear points.
- Equal chords of a circle (or of congruent circles) are equidistant from the centre (or corresponding centres).
- Chords equidistant from the centre (or corresponding centres) of a circle (or of congruent circles) are equal.
- If two arcs of a circle are congruent, then their corresponding chords are equal and conversely if two chords of a circle are equal, then their corresponding arcs (minor, major) are congruent.
- Congruent arcs of a circle subtend equal angles at the centre.
- The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
- Angles in the same segment of a circle are equal.
- Angle in a semicircle is a right angle.
- If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle.
- The sum of either pair of opposite angles of a cyclic quadrilateral is 1800.
- If sum of a pair of opposite angles of a quadrilateral is 1800, the quadrilateral is cyclic.
Activities
A discussion on “Life without circular shaped figures.”
Discussion based activity to relate and assimilate circular shapes seen in our surroundings.
Circle as a shape
A circle is the set of all points in the plane that are a fixed distance from a fixed point.
Is circle a Polygon ? - A debate
A polygon when increased in number of sides tends to form a circle is shown with this interesting activity.
Concentric circles
Drawing concentric circles, with this hands on activity circle as a shape and variations in it is explored.
Congruent circles
Equal circles are circles with same radius is a concepts that is introduced in this activity.
Equal parts in a circle
Dividing a circle in to parts and exploring to divide it into equal parts is show in this activity.
Pi the mathematical constant
Learning Objective
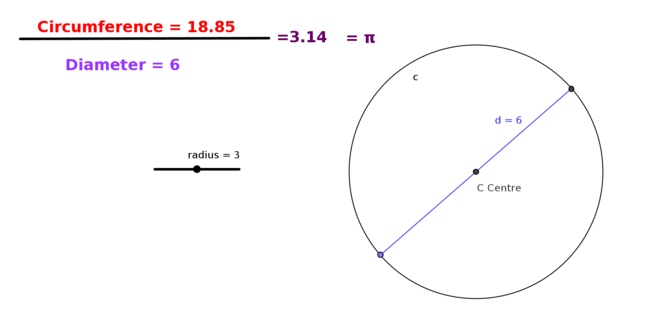
Show that the ratio of the circumference of a circle to its diameter is a constant value – Pi
Material and Resources Required
Projector, Pencil, Paper
Pre-requisites/Instructions
First for a circle of diameter 1 unit show the Geogebra file
[[1]]
To demonstrate the value of Pi move the slider named a from minimum to maxiumum value and observe the circumference
Evaluation
Use the GeoGebra file [[2]] and illustrate and verify that the ratio is true for different radius by moving the radius slider and using the table below to compute the values.
| Radius of circle r | Circumference of Circle C | C/2r |
| 6 | 18.85 | - |
| 2.5 | 15.71 | - |
| ......... | - | - |
Perimeter of a circle
Learning Objectives
To apply the use of calculating the perimeter of a circle in a real life example .
Material and Resources Required
Pencil, Paper
Pre-requisites/Instructions
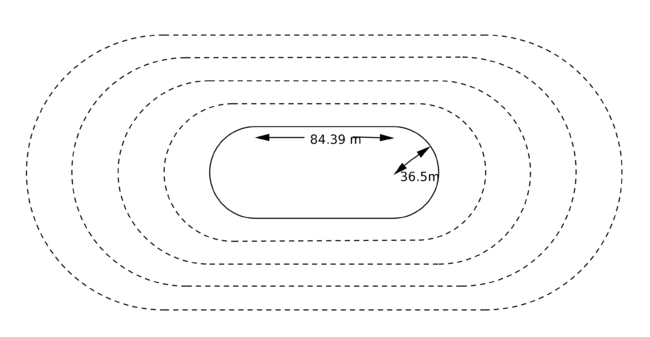
Draw the following sketch and do the calculations for the evaluation questions. The sketch shows the two main dimensions of a standard 400 metres running track.
Evaluation
- Calculate the inside perimeter of this shape.
- Why do you think that it is not equal to 400 metres? The inside runner cannot run at the very edge of the lane (there is normally an inside kerb) but let us assume that the athlete runs at a constant distance of, say, x cm from the inside edge.
- What is the radius of the two circular parts run by the athlete in the inside lane?
- Show that the total distance travelled, in centimetres, is 2 π (3650 + x ) + 16878 and equate this to 40 000 cm to find a value for x.
- Is it realistic? For 200 m and 400 m races, the runners run in specified lanes. Clearly, the further out you are the further you have to run, unless the starting positions are staggered.
- The width of each lane is 1.22 m, and it is assumed that all runners (except the inside one) run about 20 cm from the inside of their lanes.
- With these assumptions, what distance does the athlete in Lane 2 cover when running one complete lap? Hence deduce the required stagger for a 400 m race.
- What should be the stagger for someone running in Lane 3 ?
- If there are 8 runners in the 400 m race, what is the stagger of the athlete in Lane 8
compare with that in Lane 1 ? Is there any advantage in being in Lane 1?
Further Explorations
1. This link gives an overview of what Pi is. [[3]]
Concept #2 Terms associated with circles
Activities
Centre of a circle
All points on a circle are at fixed distance from a point, which is the center of a circle.
Radius and diameter of a circle
Marking radius and diameter of a circle and understand their relation.
Circumference of a circle
Measuring circumference to understand it as the perimeter of the shape.
Semicircle
Partitioning a circle into two halves to form semicircles by drawing diameter.
Interior and exterior of a circle
Points on the planar surface of the circle within its circumference are said to be interior points and points on the outside of circumference are said to be its exterior points.
Basic elements of a circle
Investigation to understand basic parameters associated with circles.
Chord of a circle
Chords of a circle are of different sizes.The length of the chord increases as it moves closer to the centre and decreases as it moves away from the center.
Arc of a circle
The part of the circumference within the two points in either directions are called its arcs.
Arcs and Sector of a circle
Slice of a circle enclosed between any two radii is called a sector.Semicircle and quadrant are special types of sectors.
Concept #3: Circles and Lines
Activities
Introduction to chords
A chord is the interval joining two distinct points on a circle. This activity investigates formation of chord and compares with the diameter of the circle.
Activity1 Angles in the same segment are equal
Angle subtended by an arc
Secant and tangent of a circle
A tangent is a line touching a circle in one point. A secant is the line through two distinct points on a circle.
Concept #4: Theorems and properties
A chord is a straight line joining 2 points on the circumference of a circle.Chords within a circle can be related in many ways.
The theorems that involve chords of a circle are :
- Perpendicular bisector of a chord passes through the centre of a circle.
- Congruent chords are equidistant from the centre of a circle.
- If two chords in a circle are congruent, then their intercepted arcs are congruent.
- If two chords in a circle are congruent, then they determine two central angles that are congruent.
Activities
Chord length and distance for centre of the circle
For a chord the distance from the centre is the perpendicular distance of the chord such that it passes through the centre.
The longest chord passes through the centre of the circle
Investigating the diameter is the longest chord of a circle.
Perpendicular bisector of a chord passes through the centre of a circle
Since every perpendicular bisector passes through the centre, the centre must lie on every one of them, so the centre must be their single common point.
Perpendicular from centre bisect the chord
Congruent chords are equidistant from the centre of a circle
In the same circle or in circles of equal radius:
• Equal chords are equidistant from the centre.
• Conversely, chords that are equidistant from the centre are equal.
Angles in a circle subtended by a chord
The angle made at the centre of a circle by the radii at the end points of a chord is called the central angle or angle subtended by a chord at the centre.
Concept #5: Cyclic Quadrilateral
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic.
Activities
Cyclic quadrilateral
A quadrilateral ABCD is called cyclic if all four vertices of it lie on a circle.In a cyclic quadrilateral the sum of opposite interior angles is 180 degrees.If the sum of a pair of opposite angles of a quadrilateral is 180, the quadrilateral is cyclic.In a cyclic quadrilateral the exterior angle is equal to interior opposite angle.
Properties of cyclic quadrilateral
Relation between the angles of a cyclic quadrilateral are explored with this hand on activity.
Concept #6 Constructions in circles
The students should know that tangent is a straight line touching the circle at one and only point.They should understand that a tangent is perpendicular to the radius of the circle.The construction protocol of a tangent.Constructing a tangent to a point on the circle.Constructing tangents to a circle from external point at a given distance.A tangent that is common to two circles is called a common tangent.A common tangent with both centres on the same side of the tangent is called a direct common tangent.A common tangent with both centres on either side of the tangent is called a transverse common tangent.
Circles_Constructions
Concept #7 Tangents
A line which touches a circle at exactly one point is called a tangent line and the point where it touches the circle is called the point of contact.
Properties of tangent
The tangent at any point of a circle is perpendicular to the radius through the point of contact. We can also conclude that at any point on a circle there can be one and only one tangent.
- Explain the theorem that if two segments from the same exterior point are tangent to a circle, then they are congruent.
- Solve for an unknown in a problem involving tangents.
- Apply properties of tangents to solve problems involving triangles circumscribed about a circle.
Tangents from a point outside the circle
The lengths of two tangents from an external point are equal.
The tangents drawn from an external point to a circle are equally inclined to the line joining the point to the centre of the circle.
Secant
A line which intersects the circle in two distinct points is called a secant line (usually referred to as a secant).
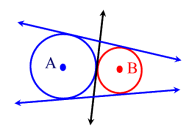
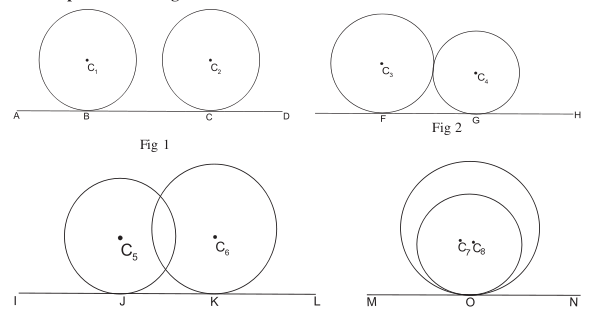
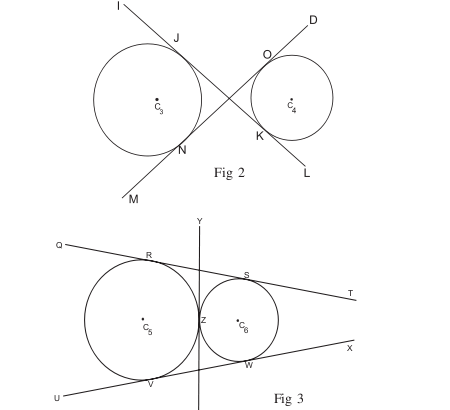
Touching circles
Common tangents
Common tangents are lines or segments that are tangent to moret han one circle at the same time.
Direct common tangents
The centres of the circles lie on the same side of the common tangent.(dct)
Transverse common tangents
The centres of the circles lie on either side of the common tangent(tct)
Evaluation
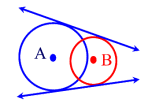
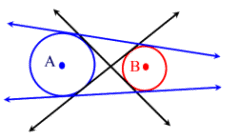
1.How many direct common tangents can be drawn to 2 intersecting circles and 2 separate circles?
2.Can you draw tct to 2 intersecting circles?
3. How many umber of tangents to a circle which are parallel to a secant ?
4. How many number of tangents that can be drawn through a point which is inside the circle ?
Proofs and verification of properties of tangents
The correct use of reasoning is at the core of mathematics, especially in constructing proofs. Many statements, especially in geometry. Recall that a proof is made up of several mathematical statements, each of which is logically deduced from a previous statement in the proof, or from a theorem proved earlier, or an axiom, or the hypotheses. The main tool, we use in constructing a proof, is the process of deductive reasoning.
We start the study of this chapter in deductive reasoning using several examples.
we can verify the theorems by practical construction. And also by using GeoGebra tool.
Tangents to a circles:
- Tangent: line that intersects a circle in exactly one point, called the point of tangency
- Radius from centre of circle to the point of tangency is always perpendicular to the tangent line. If
- The radius is not perpendicular to the line, the line is not tangent to the circle.
- Recall the Pythagorean Theorem:
- Use the fact that a tangent line and the radius through that point of tangency are perpendicular to solve for a third value. Show how you can also use this fact to deduce whether or not a line is tangent to a specific circle.
- Tangents from an external point are equal in length.
Tangents to a circle -Activity
Construction of tanget to a circle and its properties
Types of tangents
- Recognise the difference between a secant and a tangent of a circle.
- Construct a tangent to a circle at a given point on it.
- Construct and verify that, the radius drawn at the point of contact is perpendicular to the tangent.
- Construct tangents to a circle from an external point.
- Recognise the properties of direct common tangents and the transverse common tangents.
Touching circles
Common tangents of two circles How many common tangents do two circles have. Informally draw all different cases, with 0, 1, 2, 3, 4 common tangents.
For any two different circles, there are five possibilities regarding their common tangents:
- One circle lies inside the other. They have no common tangents.
- One circle touches the other from inside. There is one common tangent, located at this touching point.
- The two circles intersect in two points. They have two common tangents, which lie symmetrically to the axis connecting the two centres.
- The two circles touch each other from outside. They have three common tangents.
- The two circles lie outside of each other. They have four common tangents.
Construction of tangents
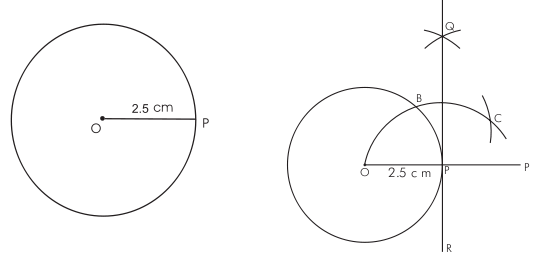
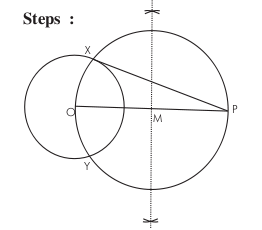
- To draw a tangent to a circle from an external point
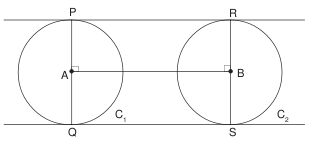
- To draw direct common tangents to two given circles of equal radii, with centres ‘d’ units apart.
- To draw a direct common tangent to two circles of different radii.
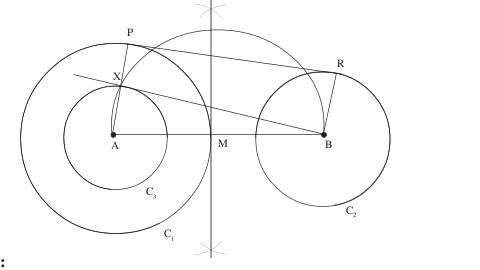
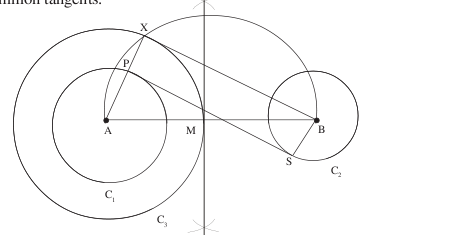
To construct Transverse common tangents to two circles.
Learning Objectives
Acquire knowledge about the
- properties of angles related to tangents.
- properties of tangents drawn to a circle from an external point and their applications.
- The angle between the tangent and a chord at the point of contact and the angle in the alternate segment and its application.
Material and Resources Required
Pencil, Paper
Pre-requisites/Instructions
Please refer to the document 22-Tangents File:2.7 Circles - Tangent Activities.pdf and complete the exercises.
Construction of direct common tangent
The direct common tangents to two circles meet on the line of centres and divide it externally in the ratio of the radii.
Construction of transverse common tangent
The transverse common tangents also meet on the line of centres and divide it internally in the ratio of the radii.
Further Explorations
1. This link gives an overview of what tangents are, [[4]]
See Also
Click here for some interesting videos on constructions of circles.
Teachers Corner
The major portion of the contributions for this topic are from Radha N, GHS Begur and Roopa N GHS Nelavagilu .
GeoGebra Contributions
- The GeoGebra file below verifies the theorem
- The angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
- Arcs and Angles http://karnatakaeducation.org.in/KOER/Maths/Arc_angle.html
- Download ggb file here http://karnatakaeducation.org.in/KOER/Maths/Arc_angle.ggb
- Arcs and Angles Part 2 http://karnatakaeducation.org.in/KOER/Maths/Same_segment_angle.html
- Download ggb file here http://karnatakaeducation.org.in/KOER/Maths/Same_segment_angle.ggb
- See a video to understand this theorem http://www.youtube.com/watch?v=0B0v0NCHZx0
- This GeoGebra file shows how a cone can be constructed from a sector of a circle
- Cone Construction http://karnatakaeducation.org.in/KOER/Maths/conesurfacearea.html
- Download ggb file here http://karnatakaeducation.org.in/KOER/Maths/conesurfacearea.ggb
Solved problems/ key questions (earlier was hints for problems).
Projects (can include math lab/ science lab/ language lab)
- Collect different types of circular objects
- Collect different Pie Charts.
- Collect different photographs of tools of cutting circles
- Collect different coins of circular shape
- Collect different images of medals