"ವಿಷಮ ಭಿನ್ನರಾಶಿ ಮತ್ತು ಮಿಶ್ರ ಭಿನ್ನರಾಶಿಗಳು" ಆವೃತ್ತಿಗಳ ಮಧ್ಯದ ಬದಲಾವಣೆಗಳು
Jump to navigation
Jump to search
| (ಅದೇ ಬಳಕೆದಾರನ ೬ ಮಧ್ಯದ ಬದಲಾವಣೆಗಳನ್ನು ತೋರಿಸುತ್ತಿಲ್ಲ) | |||
| ೪ ನೇ ಸಾಲು: | ೪ ನೇ ಸಾಲು: | ||
ಅಂಶವು ಛೇದಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿರುವ ಭಿನ್ನರಾಶಿಗಳನ್ನು ವಿಷಮ ಭಿನ್ನರಾಶಿಗಳು ಎಂದು ಕರೆಯುತ್ತೇವೆ. <math>\frac{3}{2},\frac{12}{7},\frac{18}{5}</math> ಮುಂತಾದ ಭಿನ್ನರಾಶಿಗಳು ವಿಷಮ ಭಿನ್ನರಾಶಿಗಳು. ವಿಷಮ ಭಿನ್ನರಾಶಿಯನ್ನು ಒಂದು ಪೂರ್ಣ ಹಾಗೂ ಒಂದು ಭಾಗದ ಸಂಯೋಜಿತ ರೂಪದಲ್ಲಿ ಬರೆಯಬಹುದು. ಇಂತಹ ಭಿನ್ನರಾಶಿಗಳನ್ನು ಮಿಶ್ರ ಭಿನ್ನರಾಶಿಗಳೆನ್ನುವರು. | ಅಂಶವು ಛೇದಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿರುವ ಭಿನ್ನರಾಶಿಗಳನ್ನು ವಿಷಮ ಭಿನ್ನರಾಶಿಗಳು ಎಂದು ಕರೆಯುತ್ತೇವೆ. <math>\frac{3}{2},\frac{12}{7},\frac{18}{5}</math> ಮುಂತಾದ ಭಿನ್ನರಾಶಿಗಳು ವಿಷಮ ಭಿನ್ನರಾಶಿಗಳು. ವಿಷಮ ಭಿನ್ನರಾಶಿಯನ್ನು ಒಂದು ಪೂರ್ಣ ಹಾಗೂ ಒಂದು ಭಾಗದ ಸಂಯೋಜಿತ ರೂಪದಲ್ಲಿ ಬರೆಯಬಹುದು. ಇಂತಹ ಭಿನ್ನರಾಶಿಗಳನ್ನು ಮಿಶ್ರ ಭಿನ್ನರಾಶಿಗಳೆನ್ನುವರು. | ||
| − | ಉದಾಹರಣೆ: <math>\frac{18}{5}</math> ಅನ್ನು | + | ಉದಾಹರಣೆ: |
| + | |||
| + | [[ಚಿತ್ರ:Mixed fraction image.png|left|thumb]] | ||
| + | |||
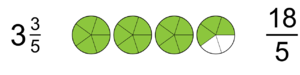
| + | <math>\frac{18}{5}</math> ಅನ್ನು 3 <math>\tfrac{3}{5}</math> ಎಂದು ಬರೆಯಲಾಗುತ್ತದೆ. | ||
| + | |||
| + | |||
| + | |||
=== ಉದ್ದೇಶಗಳು === | === ಉದ್ದೇಶಗಳು === | ||
| − | * ಭಿನ್ನರಾಶಿಯ | + | * ಭಿನ್ನರಾಶಿಯ ಅಂಶ ಮತ್ತು ಛೇದವನ್ನು ಬದಲಾಯಿಸಿದಾಗ ಭಿನ್ನರಾಶಿಯ ಮೌಲ್ಯದ ಮೇಲೆ ಹೇಗೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ ಎಂಬುದನ್ನು ತಿಳಿಯುವುದು |
| − | + | * ವಿಷಮ ಮತ್ತು ಮಿಶ್ರ ಭಿನ್ನರಾಶಿಯ ಒಳ ಅರ್ಥವನ್ನು ಅರಿಯುವುದು. | |
| − | * | ||
| − | |||
=== ಸಂಪನ್ಮೂಲಗಳು === | === ಸಂಪನ್ಮೂಲಗಳು === | ||
| + | |||
| + | |||
| + | ಜಿಯೋಜಿಬ್ರಾ ಸಂಪನ್ಮೂಲ: | ||
| + | |||
| + | {{Geogebra|pctx7vcw}} | ||
| + | |||
| + | '''Credit''' : Resource Author: EDC in Maine | ||
| + | |||
ಫೆಟ್ ಸಿಮ್ಯೂಲೆಷನ್ : | ಫೆಟ್ ಸಿಮ್ಯೂಲೆಷನ್ : | ||
೧೪:೩೩, ೨೦ ನವೆಂಬರ್ ೨೦೨೪ ದ ಇತ್ತೀಚಿನ ಆವೃತ್ತಿ
ವಿಷಮ ಮತ್ತು ಮಿಶ್ರ ಭಿನ್ನರಾಶಿಗಳು
ಅಂಶವು ಛೇದಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿರುವ ಭಿನ್ನರಾಶಿಗಳನ್ನು ವಿಷಮ ಭಿನ್ನರಾಶಿಗಳು ಎಂದು ಕರೆಯುತ್ತೇವೆ. ಮುಂತಾದ ಭಿನ್ನರಾಶಿಗಳು ವಿಷಮ ಭಿನ್ನರಾಶಿಗಳು. ವಿಷಮ ಭಿನ್ನರಾಶಿಯನ್ನು ಒಂದು ಪೂರ್ಣ ಹಾಗೂ ಒಂದು ಭಾಗದ ಸಂಯೋಜಿತ ರೂಪದಲ್ಲಿ ಬರೆಯಬಹುದು. ಇಂತಹ ಭಿನ್ನರಾಶಿಗಳನ್ನು ಮಿಶ್ರ ಭಿನ್ನರಾಶಿಗಳೆನ್ನುವರು.
ಉದಾಹರಣೆ:
ಅನ್ನು 3 ಎಂದು ಬರೆಯಲಾಗುತ್ತದೆ.
ಉದ್ದೇಶಗಳು
- ಭಿನ್ನರಾಶಿಯ ಅಂಶ ಮತ್ತು ಛೇದವನ್ನು ಬದಲಾಯಿಸಿದಾಗ ಭಿನ್ನರಾಶಿಯ ಮೌಲ್ಯದ ಮೇಲೆ ಹೇಗೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ ಎಂಬುದನ್ನು ತಿಳಿಯುವುದು
- ವಿಷಮ ಮತ್ತು ಮಿಶ್ರ ಭಿನ್ನರಾಶಿಯ ಒಳ ಅರ್ಥವನ್ನು ಅರಿಯುವುದು.
ಸಂಪನ್ಮೂಲಗಳು
ಜಿಯೋಜಿಬ್ರಾ ಸಂಪನ್ಮೂಲ:
Download this geogebra file from this link.
Credit : Resource Author: EDC in Maine
ಫೆಟ್ ಸಿಮ್ಯೂಲೆಷನ್ :
ಈ ಸಿಮ್ಯೂಲೇಷನ್ ನಲ್ಲಿ ವಿವಿಧ ಭಿನ್ನರಾಶಿಗಳನ್ನು ನಿರ್ಮಿಸಬಹುದು ಮತ್ತು ಅದನ್ನು ವೃತ್ತ, ಆಯತ, ಸಿಲಿಂಡರ್, ಕೇಕ್ ನಲ್ಲಿ ಮತ್ತು ಸಂಖ್ಯಾರೇಖೆಯ ಮೇಲೆ ಪ್ರತಿನಿಧಿಸುವುದನ್ನು ನೋಡಬಹುದು. ಅದರಲ್ಲಿ ಅಂಶ ಮತ್ತು ಛೇದವನ್ನು ಗಮನಿಸಿ, ವಿಷಮ ಭಿನ್ನರಾಶಿಯನ್ನು ಪರಿಚಯಿಸಿ ಹಾಗೇ ಅದನ್ನು ಮಿಶ್ರ ಭಿನ್ನರಾಶಿಯಲ್ಲಿ ಹೇಗೆ ಬರೆಯುವುದೆಂದು ಚರ್ಚಿಸಿ.