Difference between revisions of "Angles"

From Karnataka Open Educational Resources
Jump to navigation Jump to search
 
(21 intermediate revisions by 7 users not shown)
Line 1: Line 1:
−
= Concept Plan =
 
−
<mm>[[angles.mm|Flash]]</mm>
 
−
<!-- This portal was created using subst:box portal skeleton  -->
 
−
<!--        BANNER ACROSS TOP OF PAGE        -->
 
 
{| id="mp-topbanner" style="width:100%;font-size:100%;border-collapse:separate;border-spacing:20px;"
 
{| id="mp-topbanner" style="width:100%;font-size:100%;border-collapse:separate;border-spacing:20px;"
 
|-
 
|-
−
|style="width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|
+
| style="width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |
−
[http://www.karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_History The Story of Mathematics]
+
[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_History The Story of Mathematics]
−
|style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|[http://www.karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Philosophy Philosophy of Mathematics]
+
| style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Philosophy Philosophy of Mathematics]
−
|style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|
+
| style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |
−
[http://www.karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Pedagogy Teaching of Mathematics]
+
[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Pedagogy Teaching of Mathematics]
−
|style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|
+
| style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |
−
[http://www.karnatakaeducation.org.in/KOER/en/index.php/Maths:_Curriculum_and_Syllabus Curriculum and Syllabus]
+
[http://karnatakaeducation.org.in/KOER/en/index.php/Maths:_Curriculum_and_Syllabus Curriculum and Syllabus]
−
|style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|
+
| style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |
−
[http://www.karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Topics Topics in School Mathematics]
+
[http://karnatakaeducation.org.in/KOER/en/index.php/Mathematics:_Topics Topics in School Mathematics]
−
|style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|
+
| style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |
−
[http://www.karnatakaeducation.org.in/KOER/en/index.php/Text_Books#Mathematics_-_Textbooks Textbooks]
+
[http://karnatakaeducation.org.in/KOER/en/index.php/Text_Books#Mathematics_-_Textbooks Textbooks]
−
|style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; "|
+
| style=" width:10%; border:none; border-radius:5px;box-shadow: 10px 10px 10px #888888; background:#f9f9ff; vertical-align:middle; text-align:center; " |
−
[http://www.karnatakaeducation.org.in/KOER/en/index.php/Maths:_Question_Papers Question Bank]
+
[http://karnatakaeducation.org.in/KOER/en/index.php/Maths:_Question_Papers Question Bank]
 
|}
 
|}
 
While creating a resource page, please click here for a resource creation [http://karnatakaeducation.org.in/KOER/en/index.php/Resource_Creation_Checklist '''checklist'''].
 
While creating a resource page, please click here for a resource creation [http://karnatakaeducation.org.in/KOER/en/index.php/Resource_Creation_Checklist '''checklist'''].
 +
 +
=== Concept Plan ===
 +
[[File:Angles.mm]]
 +
<!-- This portal was created using subst:box portal skeleton  -->
 +
<!--        BANNER ACROSS TOP OF PAGE        -->
  
 
__FORCETOC__
 
__FORCETOC__
Line 33: Line 34:
 
= Teaching Outlines =
 
= Teaching Outlines =
  
−
==Concept #1.What is an angle ? ==
+
====Concept #1.What is an angle ? ====
−
===Learning objectives===
+
===Activities===
−
===Notes for teachers===
+
Foramtion of
−
===Activity No # ===
 
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
−
*Estimated Time
+
*
−
*Materials/ Resources needed
 
−
*Prerequisites/Instructions, if any
 
−
*Multimedia resources
 
−
*Website interactives/ links/ / Geogebra Applets
 
−
*Process/ Developmental Questions
 
−
*Evaluation
 
−
*Question Corner
 
−
 
 
−
===Activity No # ===
 
−
{| style="height:10px; float:right; align:center;"
 
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
−
|}
 
−
*Estimated Time
 
−
*Materials/ Resources needed
 
−
*Prerequisites/Instructions, if any
 
−
*Multimedia resources
 
−
*Website interactives/ links/ / Geogebra Applets
 
−
*Process/ Developmental Questions
 
−
*Evaluation
 
−
*Question Corner
 
  
 
==Concept #2. Using a Protractor- Measuring an angle ==
 
==Concept #2. Using a Protractor- Measuring an angle ==
Line 70: Line 49:
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
 
*Estimated Time
 
*Estimated Time
Line 84: Line 63:
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
 
*Estimated Time
 
*Estimated Time
Line 98: Line 77:
 
===Learning objectives===
 
===Learning objectives===
 
===Notes for teachers===
 
===Notes for teachers===
−
===Activity No # ===
+
===Activity No #1.Crazy  Angles  using Geogebra  ===
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
−
*Estimated Time
+
*Estimated Time: 40 minutes
−
*Materials/ Resources needed
+
*Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
−
*Prerequisites/Instructions, if any
+
*Prerequisites/Instructions, if any:
−
*Multimedia resources
+
# The students should have a basic understanding about  point, rays, line segments and vertex.
 +
# They should know how angles are formed.
 +
# They should know that angles are measured in units called degrees. 360 ° is a full rotation (a circle)
 +
# They should know to use a protractor and measure the  angles.
 +
# They should know the meaning of terms acute, obtuse, straight, reflex, and complete angles.
 +
*Multimedia resources; Laptop
 
*Website interactives/ links/ / Geogebra Applets
 
*Website interactives/ links/ / Geogebra Applets
−
*Process/ Developmental Questions
+
<span> </span>
−
*Evaluation
+
 
−
*Question Corner
+
<span></span><div id="ggbContainer4a44ef2dc4b78417b74d34b3b537830b"></div><span></span>
−
===Activity No # ===
+
*Process:
−
{| style="height:10px; float:right; align:center;"
+
# The teacher should recaptulate the concept of a point, line segment, ray, vertex and angles.
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
+
# The teacher should show how angles are formed.
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
# Discuss the concept of  cartesian plane, X and Y axes, rotation, and how it relates to angles.
−
|}
+
# Demonstrate how to measure angles using a protractor.
−
*Estimated Time
+
# Define and illustrate the classification of the types of angles—acute, obtuse, right, straight zero and complete angles.
−
*Materials/ Resources needed
+
# In the succeeding class give the students protractors and let them have enough practise measuring  and classifying angles.
−
*Prerequisites/Instructions, if any
+
Developmental Questions:
−
*Multimedia resources
+
# What is a point ?
−
*Website interactives/ links/ / Geogebra Applets
+
# A minimum of how many points are needed to define a line segment ?
−
*Process/ Developmental Questions
+
# A minimum of how many points are needed to form an angle ?
−
*Evaluation
+
# Name the line segments from the figure.
−
*Question Corner
+
# What is a vertex ?
−
===Activity No # ===
+
# How many rays /line segments are needed to form an angle ? 
−
{| style="height:10px; float:right; align:center;"
+
# Name the vertex at which the angle is formed
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
+
# Name the angle .
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
# Name the type of angle formed.
−
|}
+
*Evaluation:
−
*Estimated Time
+
# Assess the students knowledge of angles by projecting different types of angles and asking    them to name
−
*Materials/ Resources needed
+
# What are the characteristics of an acute angle ?
−
*Prerequisites/Instructions, if any
+
# What are the characteristics of an obtuse angle?
−
*Multimedia resources
+
# What are the characteristics of a right angle
−
*Website interactives/ links/ / Geogebra Applets
+
# Evaluate if the students have understood that :
−
*Process/ Developmental Questions
+
*An angle is formed where 2 lines meet at a point.
−
*Evaluation
+
*A right angle looks like a corner of a square or a rectangle.
−
*Question Corner
+
*An acute angle is narrower than a right angle.
−
==Concept #3. Angle constructions==
+
*An obtuse angle is wider than a right angle.
 +
*Question Corner:
 +
# What is an angle ?
 +
# Where do you name an angle ?
 +
# How do you identify different types of angles in 2-dimensional figures?
 +
# How do angles help to classify 2-dimensional figures?
 +
# Are angles <ABA' and <A'BA the same ? Justify
 +
# Differentiate between the zero angle and a complete angle.
 +
 
 +
==Concept # 4. Angle constructions==
 
===Learning objectives===
 
===Learning objectives===
 
===Notes for teachers===
 
===Notes for teachers===
 
===Activity No # ===
 
===Activity No # ===
−
{| style="height:10px; float:right; align:center;"
+
==Concept # 5. Angle bisector-Its construction==
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
−
|}
 
−
*Estimated Time
 
−
*Materials/ Resources needed
 
−
*Prerequisites/Instructions, if any
 
−
*Multimedia resources
 
−
*Website interactives/ links/ / Geogebra Applets
 
−
*Process/ Developmental Questions
 
−
*Evaluation
 
−
*Question Corner
 
−
 
 
−
===Activity No # ===
 
−
{| style="height:10px; float:right; align:center;"
 
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
−
|}
 
−
*Estimated Time
 
−
*Materials/ Resources needed
 
−
*Prerequisites/Instructions, if any
 
−
*Multimedia resources
 
−
*Website interactives/ links/ / Geogebra Applets
 
−
*Process/ Developmental Questions
 
−
*Evaluation
 
−
*Question Corner
 
−
 
 
−
==Concept # 4. Angle bisector-Its construction==
 
 
===Learning objectives===
 
===Learning objectives===
 
===Notes for teachers===
 
===Notes for teachers===
−
===Activity No # ===
+
Activity - [[Activity-construction of angles|Construction of angle with measure 22.5∘]]
−
{| style="height:10px; float:right; align:center;"
 
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
−
|}
 
−
*Estimated Time
 
−
*Materials/ Resources needed
 
−
*Prerequisites/Instructions, if any
 
−
*Multimedia resources
 
−
*Website interactives/ links/ / Geogebra Applets
 
−
*Process/ Developmental Questions
 
−
*Evaluation
 
−
*Question Corner
 
  
−
===Activity No # ===
+
This activity helps to illustrate the 'angle bisector' construction three times since we construct ∡22.5 by constructing ∡90∘ (bisecting a segment / straight angle ∡180∘, then bisect ∡90∘ to get ∡45∘ and finally bisect ∡45∘ to get ∡22.5∘).
−
{| style="height:10px; float:right; align:center;"
 
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
−
|}
 
−
*Estimated Time
 
−
*Materials/ Resources needed
 
−
*Prerequisites/Instructions, if any
 
−
*Multimedia resources
 
−
*Website interactives/ links/ / Geogebra Applets
 
−
*Process/ Developmental Questions
 
−
*Evaluation
 
−
*Question Corner
 
  
−
==Concept # 5. Pairs of angles==
+
==Concept # 6. Pairs of angles==
 
===Learning objectives===
 
===Learning objectives===
 
===Notes for teachers===
 
===Notes for teachers===
Line 205: Line 147:
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
 
*Estimated Time
 
*Estimated Time
Line 218: Line 160:
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
 
*Estimated Time
 
*Estimated Time
Line 231: Line 173:
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
 
*Estimated Time
 
*Estimated Time
Line 241: Line 183:
 
*Evaluation
 
*Evaluation
 
*Question Corner
 
*Question Corner
−
==Concept # 6.Angles formed when lines are cut by a transversal==
+
==Concept # 7.Angles formed when lines are cut by a transversal==
 
===Learning objectives===
 
===Learning objectives===
 
===Notes for teachers===
 
===Notes for teachers===
−
'''===Activity No # 1.Angles formed when a transversal intersects parallel lines ==='''
+
'''Activity No # 1.Angles formed when a transversal intersects parallel lines '''
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
 
'''*Estimated Time :''' 40 minutes<br>
 
'''*Estimated Time :''' 40 minutes<br>
−
'''*Materials/ Resources needed :'''Laptop, geogebra file, projector and pointer.
+
'''*Materials/ Resources needed :'''Laptop, geogebra file, projector and pointer.<br>
 
'''*Prerequisites/Instructions, if any :'''
 
'''*Prerequisites/Instructions, if any :'''
 
#The students should have prior knowledge of parallel lines , transversal, angles and types of angles formed when a pair of parallel lines are intersected by a transversal.
 
#The students should have prior knowledge of parallel lines , transversal, angles and types of angles formed when a pair of parallel lines are intersected by a transversal.
Line 257: Line 199:
 
'''*Multimedia resources:'''
 
'''*Multimedia resources:'''
 
Laptop<br>
 
Laptop<br>
−
'''*Website interactives/ links/ / Geogebra Applets'''
+
'''*Website interactives/ links/ / Geogebra Applets'''<br>
 +
<span> </span>
 +
 
 +
<span></span><div id="ggbContainer507e2592e2313aaf5f5d11fe1655c6bb"></div><span></span>
 +
 
 +
* This is a resource file on 'vertically opposite angles'
 +
{{#widget:YouTube|id=m7v2g9_3BdU|left}}<br>
 +
 
 +
It has been created by Sucheta, Mathematics teacher, GHS Thyamangondlu
 +
 
 
'''*Process:'''
 
'''*Process:'''
 
#Reiterate that when a transversal  intersects parallel lines, several pairs of congruent and supplementary angles are formed.
 
#Reiterate that when a transversal  intersects parallel lines, several pairs of congruent and supplementary angles are formed.
Line 270: Line 221:
 
*Alternate exterior angles - congruent<br>
 
*Alternate exterior angles - congruent<br>
 
*Same side exterior angles - supplementary
 
*Same side exterior angles - supplementary
−
'''Developmental Questions :(What discussion questions)'''         
+
'''*Developmental Questions :(What discussion questions)'''         
 
#How many pairs of corresponding angles are there ?
 
#How many pairs of corresponding angles are there ?
 
#What is true about corresponding angles formed when parallel lines are cut by a transversal?
 
#What is true about corresponding angles formed when parallel lines are cut by a transversal?
Line 289: Line 240:
 
# Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines.
 
# Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines.
  
−
===Activity No # ===
+
==='''Activity No 2  Angles formed when a transversal intersects parallel lines'''  ===
 
{| style="height:10px; float:right; align:center;"
 
{| style="height:10px; float:right; align:center;"
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
 
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
 
|}
 
|}
−
*Estimated Time
+
*'''Estimated Time''' : 90 minutes
−
*Materials/ Resources needed
+
*'''Materials/ Resources needed'''
−
*Prerequisites/Instructions, if any
+
Laptop, geogebra file, projector and pointer.
−
*Multimedia resources
+
*'''Prerequisites/Instructions, if any'''
−
*Website interactives/ links/ / Geogebra Applets
+
#The students should have prior knowledge of parallel lines , transversal, angles and types of angles formed when a pair of parallel lines are intersected by a transversal.
−
*Process/ Developmental Questions
+
#They should know what the terms interior, exterior, adjacent, alternate, consecutive, congruent, linear and corresponding mean.
−
*Evaluation
+
#Students should know the definition of complementary angles, supplementary angles, and congruent angles.
−
*Question Corner
+
*'''Multimedia resources''':
−
===Activity No # ===
+
Laptop
−
{| style="height:10px; float:right; align:center;"
+
*'''Website interactives/ links/ / Geogebra Applets'''
−
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;">
+
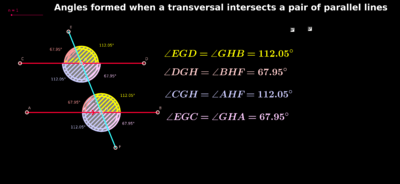
[[File:111.png|400px]]
−
''[http://www.karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div>
+
*'''Process'''
−
|}
+
#Reiterate that when a transversal  intersects parallel lines, several pairs of congruent and supplementary angles are formed.
−
*Estimated Time
+
#Have students draw two parallel lines and a third line(transversal) intersecting those two lines on their own paper. Direct them to think about any angle relationships they see. Have them discuss their conjectures with a partner.
−
*Materials/ Resources needed
+
#The teacher can next  project the GeoGebra worksheet and discuss about types of angles and their relationships with the class .
−
*Prerequisites/Instructions, if any
+
#Finally the teacher and students can summarize together the angle relationships.<br>
−
*Multimedia resources
+
Linear pair of angles - adjacent and supplementary<br>
−
*Website interactives/ links/ / Geogebra Applets
+
Vertical angles - congruent<br>
−
*Process/ Developmental Questions
+
Corresponding angles -congruent<br>
−
*Evaluation
+
Alternate interior angles - congruent<br>
−
*Question Corner
+
Same side interior angles - supplementary<br>
−
 
+
Alternate exterior angles - congruent<br>
−
 
+
Same side exterior angles - supplementary<br>
  
 +
*'''Developmental Questions'''
 +
#How many pairs of corresponding angles are there ?
 +
#What is true about corresponding angles formed when parallel lines are cut by a transversal?
 +
#Compare different pairs of alternate interior angles. What do you notice?
 +
#<EGD and <AHF are alternate exterior angles. What is another pair of alternate exterior angles?
 +
#Compare different pairs of same-side interior angles. What do you notice?
 +
#Compare different pairs of same-side exterior angles. What do you notice?
  
 +
'''Evaluation'''
 +
#What are the characteristics of linear angles (adjacent and supplementary) ?
 +
#What do you observe about the angle measures of the linear angles?
  
 +
*'''Question Corner'''
 +
#What do adjacent , alternate, linear , corresponding and consecutive mean individually
 +
#What are complementary angles?
 +
#What are supplementary angles ?
 +
#What does it mean if two angles are congruent?
 +
#What is the complement of 65 degrees
 +
#What is the supplement of 70 degrees?
 +
#Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines.
  
 
= Hints for difficult problems =
 
= Hints for difficult problems =
Line 330: Line 299:
  
 
Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template
 
Create a new page and type <nowiki>{{subst:Math-Content}}</nowiki> to use this template
 +
 +
[[Category:Lines and Angles]]

Latest revision as of 10:56, 2 November 2019

The Story of Mathematics

Philosophy of Mathematics

Teaching of Mathematics

Curriculum and Syllabus

Topics in School Mathematics

Textbooks

Question Bank

While creating a resource page, please click here for a resource creation checklist.

Concept Plan

[maximize]


Textbook

To add textbook links, please follow these instructions to: (Click to create the subpage)

Additional Information

Useful websites

Reference Books

Teaching Outlines

Concept #1.What is an angle ?

Activities

Foramtion of

Concept #2. Using a Protractor- Measuring an angle

Learning objectives

Notes for teachers

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ / Geogebra Applets
  • Process/ Developmental Questions
  • Evaluation
  • Question Corner

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ / Geogebra Applets
  • Process/ Developmental Questions
  • Evaluation
  • Question Corner

Concept #3.Types of angles

Learning objectives

Notes for teachers

Activity No #1.Crazy Angles using Geogebra

  • Estimated Time: 40 minutes
  • Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
  • Prerequisites/Instructions, if any:
  1. The students should have a basic understanding about point, rays, line segments and vertex.
  2. They should know how angles are formed.
  3. They should know that angles are measured in units called degrees. 360 ° is a full rotation (a circle)
  4. They should know to use a protractor and measure the angles.
  5. They should know the meaning of terms acute, obtuse, straight, reflex, and complete angles.
  • Multimedia resources; Laptop
  • Website interactives/ links/ / Geogebra Applets

  • Process:
  1. The teacher should recaptulate the concept of a point, line segment, ray, vertex and angles.
  2. The teacher should show how angles are formed.
  3. Discuss the concept of cartesian plane, X and Y axes, rotation, and how it relates to angles.
  4. Demonstrate how to measure angles using a protractor.
  5. Define and illustrate the classification of the types of angles—acute, obtuse, right, straight zero and complete angles.
  6. In the succeeding class give the students protractors and let them have enough practise measuring and classifying angles.

Developmental Questions:

  1. What is a point ?
  2. A minimum of how many points are needed to define a line segment ?
  3. A minimum of how many points are needed to form an angle ?
  4. Name the line segments from the figure.
  5. What is a vertex ?
  6. How many rays /line segments are needed to form an angle ?
  7. Name the vertex at which the angle is formed
  8. Name the angle .
  9. Name the type of angle formed.
  • Evaluation:
  1. Assess the students knowledge of angles by projecting different types of angles and asking them to name
  2. What are the characteristics of an acute angle ?
  3. What are the characteristics of an obtuse angle?
  4. What are the characteristics of a right angle
  5. Evaluate if the students have understood that :
  • An angle is formed where 2 lines meet at a point.
  • A right angle looks like a corner of a square or a rectangle.
  • An acute angle is narrower than a right angle.
  • An obtuse angle is wider than a right angle.
  • Question Corner:
  1. What is an angle ?
  2. Where do you name an angle ?
  3. How do you identify different types of angles in 2-dimensional figures?
  4. How do angles help to classify 2-dimensional figures?
  5. Are angles <ABA' and <A'BA the same ? Justify
  6. Differentiate between the zero angle and a complete angle.

Concept # 4. Angle constructions

Learning objectives

Notes for teachers

Activity No #

Concept # 5. Angle bisector-Its construction

Learning objectives

Notes for teachers

Activity - Construction of angle with measure 22.5∘

This activity helps to illustrate the 'angle bisector' construction three times since we construct ∡22.5 by constructing ∡90∘ (bisecting a segment / straight angle ∡180∘, then bisect ∡90∘ to get ∡45∘ and finally bisect ∡45∘ to get ∡22.5∘).

Concept # 6. Pairs of angles

Learning objectives

Notes for teachers

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ / Geogebra Applets
  • Process/ Developmental Questions
  • Evaluation
  • Question Corner

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ / Geogebra Applets
  • Process/ Developmental Questions
  • Evaluation
  • Question Corner

Activity No #

  • Estimated Time
  • Materials/ Resources needed
  • Prerequisites/Instructions, if any
  • Multimedia resources
  • Website interactives/ links/ / Geogebra Applets
  • Process/ Developmental Questions
  • Evaluation
  • Question Corner

Concept # 7.Angles formed when lines are cut by a transversal

Learning objectives

Notes for teachers

Activity No # 1.Angles formed when a transversal intersects parallel lines

*Estimated Time : 40 minutes
*Materials/ Resources needed :Laptop, geogebra file, projector and pointer.
*Prerequisites/Instructions, if any :

  1. The students should have prior knowledge of parallel lines , transversal, angles and types of angles formed when a pair of parallel lines are intersected by a transversal.
  2. They should know what the terms interior, exterior, adjacent, alternate, consecutive, congruent, linear and corresponding mean.
  3. Students should know the definition of complementary angles, supplementary angles, and congruent angles.

*Multimedia resources: Laptop
*Website interactives/ links/ / Geogebra Applets

  • This is a resource file on 'vertically opposite angles'


It has been created by Sucheta, Mathematics teacher, GHS Thyamangondlu

*Process:

  1. Reiterate that when a transversal intersects parallel lines, several pairs of congruent and supplementary angles are formed.
  2. Have students draw two parallel lines and a third line(transversal) intersecting those two lines on their own paper. Direct them to think about any angle relationships they see. Have them discuss their conjectures with a partner.
  3. The teacher can next project the GeoGebra worksheet and discuss about types of angles and their relationships with the class .
  4. Finally the teacher and students can summarize together the angle relationshipsalong with their characteristics.

Linear pair of angles - adjacent and supplementary

  • Vertical angles - congruent
  • Corresponding angles -congruent
  • Alternate interior angles - congruent
  • Same side interior angles - supplementary
  • Alternate exterior angles - congruent
  • Same side exterior angles - supplementary

*Developmental Questions :(What discussion questions)

  1. How many pairs of corresponding angles are there ?
  2. What is true about corresponding angles formed when parallel lines are cut by a transversal?
  3. Compare different pairs of alternate interior angles. What do you notice?
  4. <EGD and <AHF are alternate exterior angles. What is another pair of alternate exterior angles?
  5. Compare different pairs of same-side interior angles. What do you notice?
  6. Compare different pairs of same-side exterior angles. What do you notice?

*Evaluation:

  1. What are the characteristics of linear angles (adjacent and supplementary) ?
  2. What do you observe about the angle measures of the linear angles?

*Question Corner:

  1. What do adjacent , alternate, linear , corresponding and consecutive mean individually
  2. What are complementary angles?
  3. What are supplementary angles ?
  4. What does it mean if two angles are congruent?
  5. What is the complement of 65 degrees
  6. What is the supplement of 70 degrees?
  7. Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines.

Activity No 2 Angles formed when a transversal intersects parallel lines

  • Estimated Time : 90 minutes
  • Materials/ Resources needed

Laptop, geogebra file, projector and pointer.

  • Prerequisites/Instructions, if any
  1. The students should have prior knowledge of parallel lines , transversal, angles and types of angles formed when a pair of parallel lines are intersected by a transversal.
  2. They should know what the terms interior, exterior, adjacent, alternate, consecutive, congruent, linear and corresponding mean.
  3. Students should know the definition of complementary angles, supplementary angles, and congruent angles.
  • Multimedia resources:

Laptop

  • Website interactives/ links/ / Geogebra Applets

111.png

  • Process
  1. Reiterate that when a transversal intersects parallel lines, several pairs of congruent and supplementary angles are formed.
  2. Have students draw two parallel lines and a third line(transversal) intersecting those two lines on their own paper. Direct them to think about any angle relationships they see. Have them discuss their conjectures with a partner.
  3. The teacher can next project the GeoGebra worksheet and discuss about types of angles and their relationships with the class .
  4. Finally the teacher and students can summarize together the angle relationships.

Linear pair of angles - adjacent and supplementary
Vertical angles - congruent
Corresponding angles -congruent
Alternate interior angles - congruent
Same side interior angles - supplementary
Alternate exterior angles - congruent
Same side exterior angles - supplementary

  • Developmental Questions
  1. How many pairs of corresponding angles are there ?
  2. What is true about corresponding angles formed when parallel lines are cut by a transversal?
  3. Compare different pairs of alternate interior angles. What do you notice?
  4. <EGD and <AHF are alternate exterior angles. What is another pair of alternate exterior angles?
  5. Compare different pairs of same-side interior angles. What do you notice?
  6. Compare different pairs of same-side exterior angles. What do you notice?

Evaluation

  1. What are the characteristics of linear angles (adjacent and supplementary) ?
  2. What do you observe about the angle measures of the linear angles?
  • Question Corner
  1. What do adjacent , alternate, linear , corresponding and consecutive mean individually
  2. What are complementary angles?
  3. What are supplementary angles ?
  4. What does it mean if two angles are congruent?
  5. What is the complement of 65 degrees
  6. What is the supplement of 70 degrees?
  7. Compare angle relationships formed by parallel lines vs. angle relationships formed by non-parallel lines.

Hints for difficult problems

Project Ideas

Math Fun

Usage

Create a new page and type {{subst:Math-Content}} to use this template

Retrieved from "https://karnatakaeducation.org.in/KOER/en/index.php?title=Angles&oldid=32263"