Difference between revisions of "A Kite and its properties"
Jump to navigation
Jump to search
m (added Category:Quadrilaterals using HotCat) |
|||
| (29 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | = A Kite and its properties = | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Learning objectives=== | ===Learning objectives=== | ||
# A kite is a quadrilateral with two distinct pairs of adjacent sides that are congruent. | # A kite is a quadrilateral with two distinct pairs of adjacent sides that are congruent. | ||
| − | # | + | # The two pairs of congruent sides meet at two different points. |
| − | # | + | # A kite can also be described as a quadrilateral with an axis of symmetry along one of its diagonals. |
| + | # Kites have a couple of properties that will help us identify them from other quadrilaterals. | ||
* The diagonals of a kite meet at a right angle.<br> | * The diagonals of a kite meet at a right angle.<br> | ||
| − | *Kites have exactly one pair of opposite angles that are congruent.<br> | + | * Kites have exactly one pair of opposite angles that are congruent.<br> |
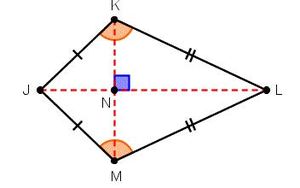
| − | + | * Diagnols intersect at right angles. | |
| − | + | <K = <M. This is the only pair of congruent angles because <J and <L have different measures. | |
| + | [[File:kite.jpeg|300px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Notes for teachers=== | ===Notes for teachers=== | ||
| − | + | Source : http://www.ask.com/question/what-is-a-kite-in-geometry<br> | |
| − | + | Summary : | |
| − | + | # A kite is sometimes also known as a deltoid. | |
| − | + | # A kite, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead". | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Activity No # 1. Paper kite=== | |
| − | |||
| − | |||
| − | ===Activity No # === | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
|<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | |<div style="width:150px;border:none; border-radius:10px;box-shadow: 5px 5px 5px #888888; background:#f5f5f5; vertical-align:top; text-align:center; padding:5px;"> | ||
| − | ''[http:// | + | ''[http://karnatakaeducation.org.in/?q=node/305 Click to Comment]''</div> |
|} | |} | ||
| − | *Estimated Time | + | *Estimated Time: 30 minutes. |
| − | *Materials/ Resources needed | + | *Materials/ Resources needed : |
| + | #A4 sheet of paper. | ||
*Prerequisites/Instructions, if any | *Prerequisites/Instructions, if any | ||
| + | # Neat paper folding skills. | ||
| + | # Ability to follow instructions. | ||
*Multimedia resources | *Multimedia resources | ||
*Website interactives/ links/ / Geogebra Applets | *Website interactives/ links/ / Geogebra Applets | ||
| − | + | This activity has been taken from the website : http://www.transum.org/software/Fun_Maths/kite/ | |
| − | * | + | *Process: |
| − | + | # Fold an A4 sheet of paper as shown in the figures to make a kite. | |
| − | + | [[File:kite 1.jpeg|200px]] [[File:kite 2.jpeg|200px]] [[File:kite 3.jpeg|200px]] [[File:kite 4.jpeg|200px]] | |
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *Developmental Questions: | |
| − | + | # Which is the figure formed ? | |
| − | + | # What is special about this quadrilateral ? | |
| − | + | # How many sides does a kite have ? | |
| − | + | # Are all sides equal ? | |
| − | + | # Mark the diagnols ? What do you notice about them ? | |
| − | * | + | *Evaluation: |
| − | + | # Were the students able dto recognise the properties of a kite. | |
| − | |||
| − | |||
| − | |||
| − | |||
*Question Corner | *Question Corner | ||
| + | # Compare kite with other quadrilaterals and make a list of similarities and differences between them. | ||
| − | + | [[Category:Quadrilaterals]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 13:55, 5 August 2020
A Kite and its properties
Learning objectives
- A kite is a quadrilateral with two distinct pairs of adjacent sides that are congruent.
- The two pairs of congruent sides meet at two different points.
- A kite can also be described as a quadrilateral with an axis of symmetry along one of its diagonals.
- Kites have a couple of properties that will help us identify them from other quadrilaterals.
- The diagonals of a kite meet at a right angle.
- Kites have exactly one pair of opposite angles that are congruent.
- Diagnols intersect at right angles.
<K = <M. This is the only pair of congruent angles because <J and <L have different measures.
Notes for teachers
Source : http://www.ask.com/question/what-is-a-kite-in-geometry
Summary :
- A kite is sometimes also known as a deltoid.
- A kite, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead".
Activity No # 1. Paper kite
- Estimated Time: 30 minutes.
- Materials/ Resources needed :
- A4 sheet of paper.
- Prerequisites/Instructions, if any
- Neat paper folding skills.
- Ability to follow instructions.
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
This activity has been taken from the website : http://www.transum.org/software/Fun_Maths/kite/
- Process:
- Fold an A4 sheet of paper as shown in the figures to make a kite.
- Developmental Questions:
- Which is the figure formed ?
- What is special about this quadrilateral ?
- How many sides does a kite have ?
- Are all sides equal ?
- Mark the diagnols ? What do you notice about them ?
- Evaluation:
- Were the students able dto recognise the properties of a kite.
- Question Corner
- Compare kite with other quadrilaterals and make a list of similarities and differences between them.