Difference between revisions of "A Kite and its properties"
Jump to navigation
Jump to search
| Line 49: | Line 49: | ||
===Notes for teachers=== | ===Notes for teachers=== | ||
| + | Source : http://www.ask.com/question/what-is-a-kite-in-geometry<br> | ||
| + | Summary : | ||
# A kite is sometimes also known as a deltoid. | # A kite is sometimes also known as a deltoid. | ||
# A kite, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead". | # A kite, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead". | ||
| + | |||
===Activity No # 1. Paper kite=== | ===Activity No # 1. Paper kite=== | ||
{| style="height:10px; float:right; align:center;" | {| style="height:10px; float:right; align:center;" | ||
Revision as of 15:54, 2 January 2014
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Error: Mind Map file kite.mm not found
Textbook
To add textbook links, please follow these instructions to: (Click to create the subpage)
Additional Information
Useful websites
- http://www.transum.org/software/Fun_Maths/kite. This website has good description and activities about kites.
Reference Books
Teaching Outlines
Concept # 1. A Kite and its properties
Learning objectives
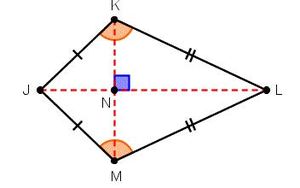
- A kite is a quadrilateral with two distinct pairs of adjacent sides that are congruent.
- The two pairs of congruent sides meet at two different points.
- A kite can also be described as a quadrilateral with an axis of symmetry along one of its diagonals.
- Kites have a couple of properties that will help us identify them from other quadrilaterals.
- The diagonals of a kite meet at a right angle.
- Kites have exactly one pair of opposite angles that are congruent.
- Diagnols intersect at right angles.
<K = <M. This is the only pair of congruent angles because <J and <L have different measures.
Notes for teachers
Source : http://www.ask.com/question/what-is-a-kite-in-geometry
Summary :
- A kite is sometimes also known as a deltoid.
- A kite, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead".
Activity No # 1. Paper kite
- Estimated Time: 30 minutes.
- Materials/ Resources needed :
- A4 sheet of paper.
- Prerequisites/Instructions, if any
- Neat paper folding skills.
- Ability to follow instructions.
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
This activity has been taken from the website : http://www.transum.org/software/Fun_Maths/kite/
- Process:
- Fold an A4 sheet of paper as shown in the figures to make a kite.
- Developmental Questions:
- Which is the figure formed ?
- What is special about this quadrilateral ?
- How many sides does a kite have ?
- Are all sides equal ?
- Mark the diagnols ? What do you notice about them ?
- Evaluation:
- Were the students able dto recognise the properties of a kite.
- Question Corner
- Compare kite with other quadrilaterals and make a list of similarities and differences between them.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept #2. Measurements in a kite
Learning objectives
- A kite has two pairs of congruent sides.
- Its diagnols intersect at right angles.
- The sum of its four sides would be its perimetre.
- Its area is given by the formula
Notes for teachers
Activity No # 1. Deriving formula for area of a kite
- Estimated Time : 30 minutes.
- Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any
- They should know a kite and its properties.
- The students should know the concept of an area.
- They should know the formula to find the area of a triangle.
- Multimedia resources: Laptop
- Website interactives/ links/ / Geogebra Applets
- Process:
- The teacher can project the geogebra file on kite.
- Show them that a kite is made of two isosceles traingles.
- Sum of areas of these two triangles would be the area of the kite.
- Developmental Questions
- What is a kite /
- What are the properties of a kite.
- What other figures can you see in a kite ?
- What types of triangles are these ?
- Identify the two isosceles triangles ?
- What is the formula to find the area of a triangle ?
- Evaluation:
- Choosing which two traingles out of the 8 visible types would be easy to deduce the area of kite ?
- Question Corner:
- Recall the two formulae that you know to find the area of a triangle.
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Concept # 3. Construction of a kite
Learning objectives
- Learn steps for constructing a kite with given measures.
Notes for teachers
Activity No # 1. Construction of a kite.
- Estimated Time : 20 minutes.
- Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
- Prerequisites/Instructions, if any:
- Students should have prior knowledge about a kite and its properties.
- They should know a perpendicular line and its construction.
- They should know to construct a line segment of given length by constructing arcs.
- Multimedia resources: Laptop
- Website interactives/ links/ / Geogebra Applets
- Process:
- The teacher can initially have a recaptualation of the concept of a kite and its properties.
- Give them measures say, "Construct a kite which has its congruent sides as 4 cm and 6 cm a pair with one of its diagnols measuring 5cm.
- Can project the geogebra file and explain the steps of construction for the given measures.
- Draw a rough small kite labelling with the given measures.
- Begin with drawing a line segment, the diagnol of a given measure, here 5 cm. label it as AB.
- Draw a perpendicular bisector to this line segment AB.
- With A as centre construct an arc with 4cm as radius. Mark the intersecting point of arc with the perpendicular bisector as D. Join AD.
- With B as centre construct another arc with the same radius 4cm. You get the same point D as point of intersection .
- Join AD and BD which would measure 4cm each and would become one pair of congruent sides of the kite.
- Similarly draw arcs on the other side taking radius as 6cm to get other pair of congruent sides.
- ADBE would be the specified kite.
- Developmental Questions:
- What are the properties of a kite ?
- What measures are given for constructing a kite ?
- By which given measure can we begin the kite construction ?
- What is the angle between the two diagnols in a kite ?
- For what purpose are we drawing the perpendicular bisector ?
- What is the purpose of drawing an arc ?
- What should be measure of the radius of the arc ?
- Why should AD and BD be same ?
- Evaluation:
- Check if the constructed kite satisfies all of its properties.
- Question Corner:
- Can you think of any other method of kite construction for the given measures ?
Activity No #
- Estimated Time
- Materials/ Resources needed
- Prerequisites/Instructions, if any
- Multimedia resources
- Website interactives/ links/ / Geogebra Applets
- Process/ Developmental Questions
- Evaluation
- Question Corner
Hints for difficult problems
Project Ideas
Math Fun
Usage
Create a new page and type {{subst:Math-Content}} to use this template