Cyclic quadrilateral

The Story of Mathematics

Philosophy of Mathematics

Teaching of Mathematics

Curriculum and Syllabus

Topics in School Mathematics

Textbooks

Question Bank

While creating a resource page, please click here for a resource creation checklist.

Concept Map

Error: Mind Map file Cyclic_quadrilateral.mm not found

Textbook

To add textbook links, please follow these instructions to: (Click to create the subpage)

Teaching Outlines

Concept # 1. Cyclic quadrilateral and its properties

Learning objectives

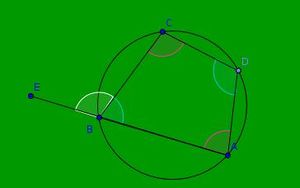
1. A quadrilateral ABCD is called cyclic if all of its four vertices lie on a circle.
2. In a cyclic quadrilateral the sum of opposite interior angles is 180 degrees.
3. If the sum of a pair of opposite angles of a quadrilateral is 180, the quadrilateral is cyclic.
4. In a cyclic quadrilateral the exterior angle is equal to interior opposite angle.

Activity#1 Cyclic quadrilateral

• Estimated Time 10 minutes
• Materials/ Resources needed: Laptop, geogebra file, projector and a pointer.
• Prerequisites/Instructions, if any

1. Circle and quadrilaterals should have been introduced.

• Multimedia resources : Laptop
• Website interactives/ links/ / Geogebra Applets

• Process:

1. The teacher can recall the concept of a circle, quadrilateral, circumcircle.
2. Can explain a cyclic quadrilateral and show the geogebra applet.
3. Move points, the vertices of the quadrilateral and let the students observe the sum of opposite interior angles.

Developmental Questions:

1. What two figures do you see in the figure ?
2. Name the vertices of the quadrilateral.
3. Where are all the 4 vertices situated ?
4. Name the opposite interior angles of the quadrilateral.
5. What do you observe about them.

• Evaluation:

1. Compare the cyclic quadrilateral to circumcircle.

• Question Corner

1. Can all quadrilaterals be cyclic ?
2. What are the necessary conditions for a quadrilateral to be cyclic ?

Activity No # 2.Properties of a Cyclic quadrilateral

• Estimated Time: 45 minutes
• Materials/ Resources needed

coloured paper, pair of scissors, sketch pen, carbon paper, geometry box

• Prerequisites/Instructions, if any

1. In a cyclic quadrilateral the sum of opposite interior angles is 180 degrees.
2. In a cyclic quadrilateral the exterior angle is equal to interior opposite angle

• Multimedia resources
• Website interactives/ links/ / Geogebra Applets

This activity has been taken from the website http://mykhmsmathclass.blogspot.in/2007/11/class-ix-activity-16.html

• Process:

1. Draw a circle of any radius on a coloured paper and cut it.
2. Paste the circle cut out on a rectangular sheet of paper.
3. By paper folding get chords AB, BC, CD and DA in order.
4. Draw AB, BC, CD & DA. A cyclic quadrilateral ABCD is obtained.
5. Produce AB to form a ray AE such that exterior angle CBE is formed.
6. Make a replica of cyclic quadrilateral ABCD using carbon paper.
7. Cut the replica into 4 parts such that each part contains one angle .
8. Draw a straight line on a paper.
9. Place the two opposite angles, angle BAD and angle BCD adjacent to each other on the straight line.Write the observation.
10. Place other two opposite angles, angle ABC and angle ADC adjacent to each other on the straight line . Write the observation.
11. Make a replica of angle ADC and place it on angle CBE . Write the observation.

Developmental Questions:

1. How do you take radius ?
2. What is the circumference ?
3. What is a chord ?
4. What is a quadrilateral ?
5. Where are all four vertices of a quadrilateral located ?
6. What part are we trying to cut and compare ?
7. What can you infer ?

• Evaluation:

1. Angle BAD and angle BCD, when placed adjacent to each other on a straight line, completely cover the straight angle.What does this mean ?
2. Angle ABC and angle ADC, when placed adjacent to each other on a straight line, completely cover the straight angle.What can you conclude ?
3. Compare angle ADC with angle CBE.

• Question Corner:

Name the two properties of cyclic quarilaterals.

Concept # 2.Construction of cyclic quadrilateral

Learning objectives

1. Ability to construct a cyclic quadrilateral accurately .

Activity No # Constructing a cyclic quadrilateral

Click to Comment

• Estimated Time: 40 minutes.
• Materials/ Resources needed:

1. Laptop, geogebra file, projector and a pointer.
2. Students constructing materials, the geometry box.
3. white papers.

• Prerequisites/Instructions, if any

1. The students should have sufficient knowledge regarding construction of perpendicular lines, bisectors, angles and circle.

• Multimedia resources : Laptop
• Website interactives/ links/ / Geogebra Applets: For step by step illustration of cyclic quadrilateral construction please refer to the website: http://www.matrusrieppower.net/Constructionoftriangleandcyclicquadrilateral.html.
• Process:

1. The teacher can do this activity after introducing the concept and properties of cyclic quadrilateral.
2. She can project the file and let students watch it carefully.
3. After watching discuss the steps of construction and the purpose of each step so that the students can appreciate the sequence of construction steps.
4. Then ask the students to actually construct a cyclic quadrilateral for the given measures.

• Developmental Questions:

1. What is a cyclic quadrilateral ? Why is it called so ?
2. Name the measuring parameters of it ?
3. What measures are given for its construction ?
4. Explain the steps involved in determing the radius of the required circle ?
5. What do the measures of the arcs specify ?

• Evaluation:

1. Were the students able to justify the sequence of steps involved ?

• Question Corner:

1. Can you draw a circle first and then the quadrilateral ? Why not so ?

Activity No #

Click to Comment

• Estimated Time
• Materials/ Resources needed
• Prerequisites/Instructions, if any
• Multimedia resources
• Website interactives/ links/ / Geogebra Applets
• Process/ Developmental Questions
• Evaluation
• Question Corner

Concept # 3. Theorems on cyclic quadrilaterals

Learning objectives

1. Both pairs of opposite angles of a cyclic quadrilateral are supplementary.
2. When one side of a cyclic quadrilateral is produced, the exterior angle so formed is equal to the interior opposite angle.
   

Converse theorems:

1. Suppose a quadrilateral is such that the sum of two opposite angles is a straight angle, them the quadrilateral is cyclic.
2. If the exterior angle of a quadrilateral is equal to the interior opposite angle, then the quadrilateral is cyclic.

Activity No 1. Theorems

Click to Comment

• Estimated Time : 40 minutes.
• Materials/ Resources needed:

Laptop, geogebra file, projector and a pointer.

• Prerequisites/Instructions, if any

1. The students should know a cyclic quadrilateral and its properties.
2. They should know the linear pair and exterior angle theorem.
3. They should know the circle theorem (Angle at centre = double the angle at the circumference)

• Multimedia resources: Laptop
• Website interactives/ links/ / Geogebra Applets:

• Process:

1. The teacher can project the geogebra file and prove the theorems.

• Developmental Questions:

1. How many angles does a cyclic quadrilateral have ?
2. Name the opposite angles of it.
3. Name the minor arc.
4. Recall the angle -arc theorem.
5. What is the total angle at the centre of a circle ?
6. Name the angles at the centre of the circle.
7. What is the sum of those two angles ?
8. How can you show that <b and <d are supplementary from above observations ?

• Evaluation;

1. What is the converse of this theorem.

• Question Corner;

1. Write down the steps to prove the converse of this theorem.

Activity No #

Click to Comment

• Estimated Time
• Materials/ Resources needed
• Prerequisites/Instructions, if any
• Multimedia resources
• Website interactives/ links/ / Geogebra Applets
• Process/ Developmental Questions
• Evaluation
• Question Corner

Math Fun

Usage

Create a new page and type {{subst:Math-Content}} to use this template