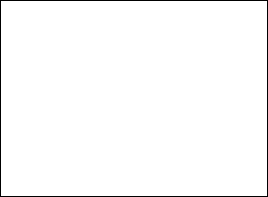Learning geogebra
6.Learning geometry with GeoGebra
Chapter objectives
In this chapter you will learn
- How you can use the computer to learn mathematics.
- About GeoGebra a mathematical software application that helps you learn Geometry, Algebra and Statistics.
- How to use GeoGebra.
- Connect GeoGebra with the geometry taught in the maths class to better understand some of the concepts and properties.
How can we use ICTs for learning mathematics?
Nowadays we see computers everywhere and we know that it has become an important part of our daily lives. So far we have learnt how to use the computer for basic document writing also called text processing. We have used the Internet to read information. We might also have watched some videos, listened to music, seen some CDs about our class lessons. You must have played some games on the computer as well! Have you seen or used a calculator? A calculator is a device to do arithmetic calculations. Now calculators are available in computers and mobile phones. Now you can also learn other areas of mathematics such as geometry, algebra and statistics using software applications like GeoGebra.
It helps you visualise geometric concepts and explore properties of
different types of geometric figures like lines, triangles and rays.
What is GeoGebra ?
Can you guess why the creators of this tool named it GeoGebra. Geo is an abbreviation for Geometry and Gebra for Algebra. Did you know that you can represent all geometric figures as algebra equations? GeoGebra helps you see both the geometric figures and its algebra representation at the same time, hence the name GeoGebra.
In this chapter you will learn to understand Geometry concepts using GeoGebra.
In GeoGebra you can animate
the geometric figure you have drawn and dynamically see how
some values like length, area, perimeter of a figure changes, see the
same figure in different ways.
Lab exercises
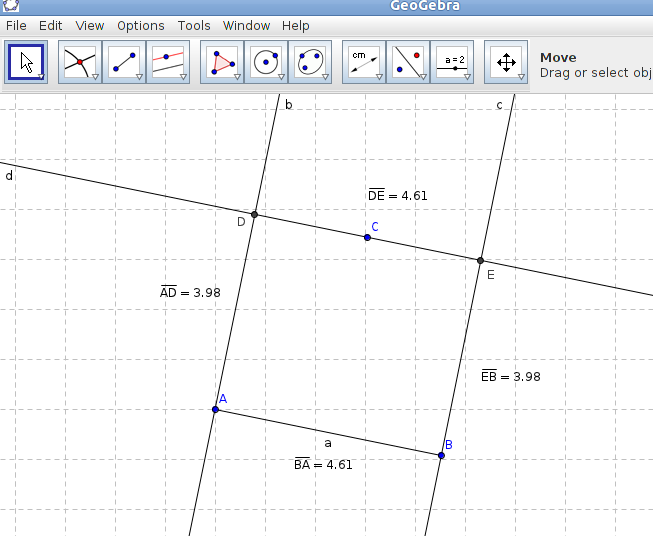
Introduction, the GeoGebra window
The GeoGebra screen is divided in several sections to represent mathematical objects in different
ways. The names of the different
parts are shown below.
Menu
Bar: It is a typical
windows command menu bar. File,
Edit, View etc...
are called the menu-items.
Tool Bar: It
has all the tools (compass
box) to use in the graphic view.
Active Tool View: It
tells you which tool is active to use on the graphic view and how to
use it.
Graphic View: It is used
to draw the geometric figures (also called objects
in GeoGebra). This window can never be closed.
Algebra View: It shows
the algebraic expressions. This window can be closed if you are
working only on geometry.
Input Bar: This
is used to enter more complex mathematical expressions that may not
be available on the Tool Bar.
Commands: It has to be used
along with the Input Bar, to select from a list of available
commands.
The Toolbar
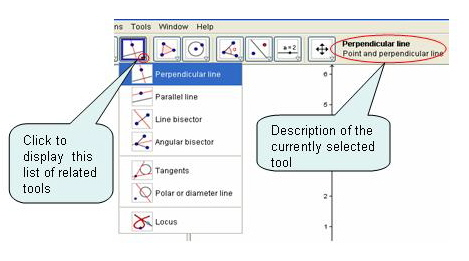
The tool bar is GeoGebra's compass box
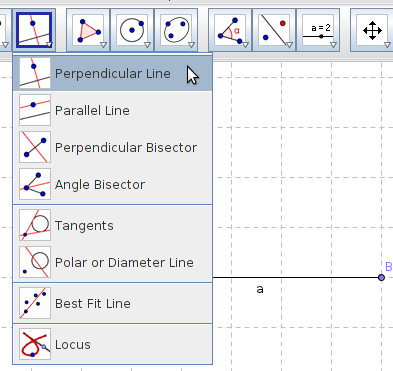
 Each tool has many related tools under it. To see all
the related tools, click on the arrow at the bottom right hand corner
of each tool as shown below.
Each tool has many related tools under it. To see all
the related tools, click on the arrow at the bottom right hand corner
of each tool as shown below.
Basic use of tools
 Activate a tool by clicking on the button showing the corresponding icon.
Activate a tool by clicking on the button showing the corresponding icon.- Open a toolbox by clicking on the lower part of a button and select another tool from this toolbox.
Look of screen
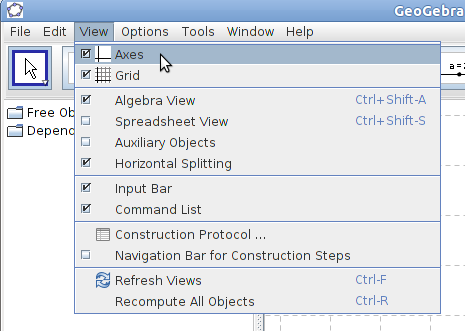 In
GeoGebra only the graphic view cannot be closed. You can change the
screen to be best fit for working with your needs: Press View
on the menu Item and uncheck or check Algebra View,
Axes and Grid based on your needs.
In
GeoGebra only the graphic view cannot be closed. You can change the
screen to be best fit for working with your needs: Press View
on the menu Item and uncheck or check Algebra View,
Axes and Grid based on your needs.
GeoGebra Exercises
- Drawing points, line segment and rays
To learn how to use GeoGebra we will
use the most commonly used tools when drawing geometrical shapes .
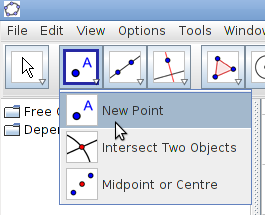
- Select Point Tool, and click anywhere on the drawing point to plot six points A, B, C, D, E, F.
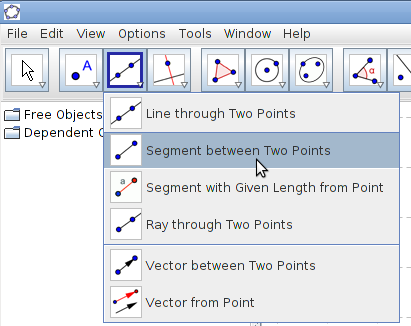
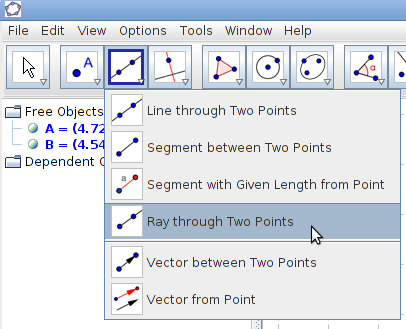 Select Segment between two points tool, click on point A and then point B.
Select Segment between two points tool, click on point A and then point B.- Select Line through two points tool, click on point C and then point D.
- Select Ray through two points tool, click on point E and the point F.
Can you describe in your own words the difference between a segment, line and ray? Also see the algebra view and observe the equations of the line b and ray c. The line segment a is represented in the algebra view as a = 2.83, where 2.83 is the length of the segment.
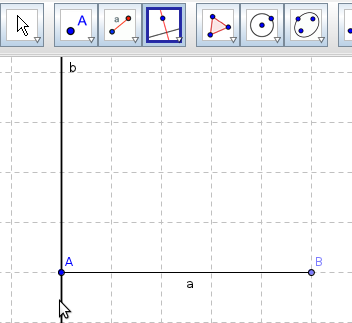
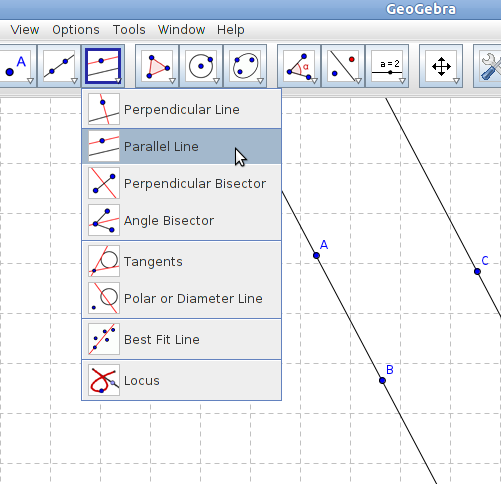 Drawing a parallel line
Drawing a parallel line
- Select Point Tool and click anywhere on the drawing point to plot three points A,B, C.
- Select Line through two points tool, click on point A and then point B.
- Select Parallel Line tool, click on point C first. Then click on line AB.
![]() Now
use the Move Tool
move points A, B and C. What do you observe? Describe it.
Now
use the Move Tool
move points A, B and C. What do you observe? Describe it.
![]() Next
use the Move Graphics view
tool and move the drawing pad. Do the two lines ever
meet?
Next
use the Move Graphics view
tool and move the drawing pad. Do the two lines ever
meet?
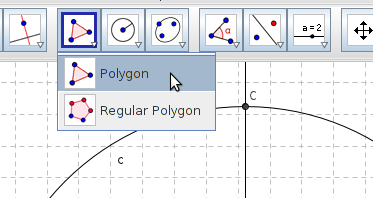
- Drawing polygons
 Try
making a pentagon and hexagon on your own.
Try
making a pentagon and hexagon on your own.
- Rotate a ray
- Draw line segment AB of any length' (Segment between two points tool)'.
- Select the Ray Through two points tool, click on point A, then select another point C on the drawing pad as shown in the figure.
- Select the Angle tool, as seen in the figure and click on points B, then A and finally C. You will see an angle measure. Click on the Move tool and move point C. Observe the change of angle.
- Observe the direction (clockwise, anticlockwise) in which you move the ray? In which direction does the angle increase and which direction does it decrease?
- Draw triangles
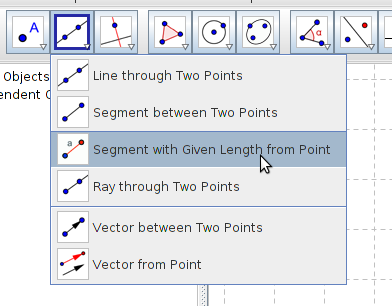
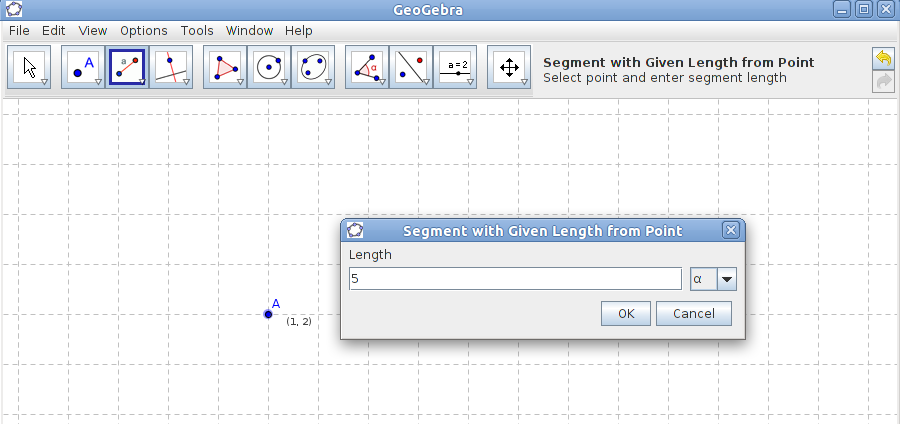
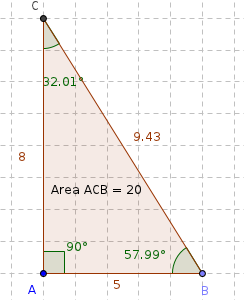
In this exercise you are going to draw a right-angled triangle where the base is 5 units and the hypotenuse is 8 units.
All buttons on the tool bar hide
many related tools. You choose the tool you want by pressing the
small red arrow in the lower right corner of the button. Choose from
the list that shows up.
- Start your drawing by using the tool Segment with Given Length from Point.
- Continue by drawing the right angle. Do this by drawing a perpendicular line through point A. Choose the perpendicular line tool, click on point A first and then on the line.
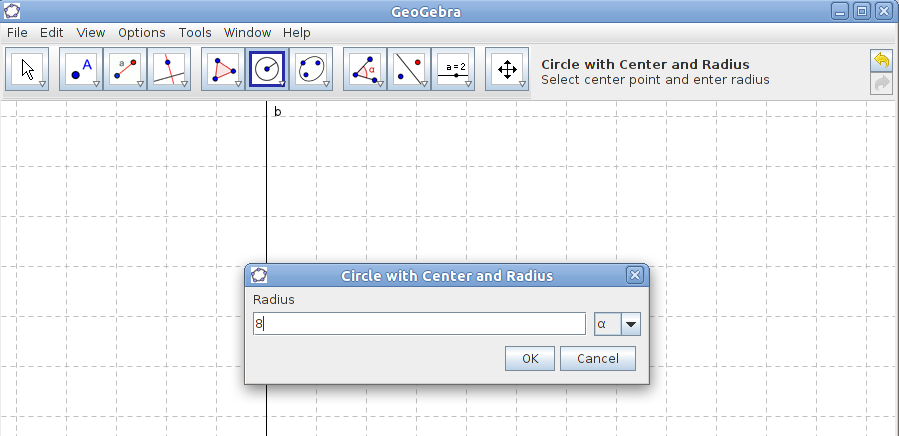
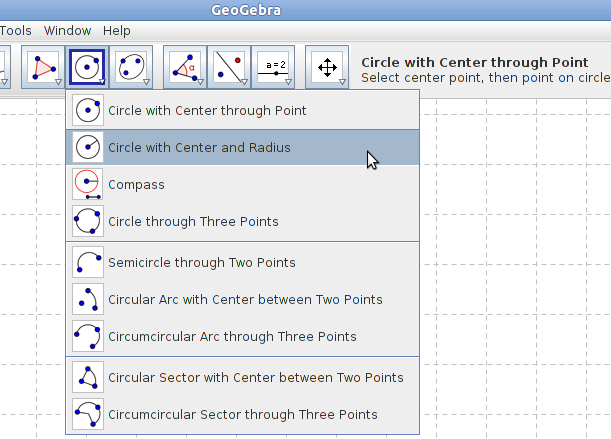 To mark the third corner of the triangle you use one of the circle tools, Circle with Centre and Radius.
To mark the third corner of the triangle you use one of the circle tools, Circle with Centre and Radius.- Click on the point B and fill in the length of the hypotenuse as radius.
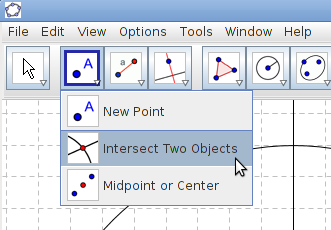 Choose the tool Intersect Two Objects, click on the circle and the perpendicular line. The point in the intersection is the third corner of the triangle.
Choose the tool Intersect Two Objects, click on the circle and the perpendicular line. The point in the intersection is the third corner of the triangle.
- Draw the triangle by choosing the Polygon tool. You need to click all the corners and then click again on the first corner to complete the triangle.
- The perpendicular line and the circle, even the points do not need to be visible or seen now, you only want to show the triangle. Hide an object by right-clicking the object and uncheck Show Object by clicking on it.
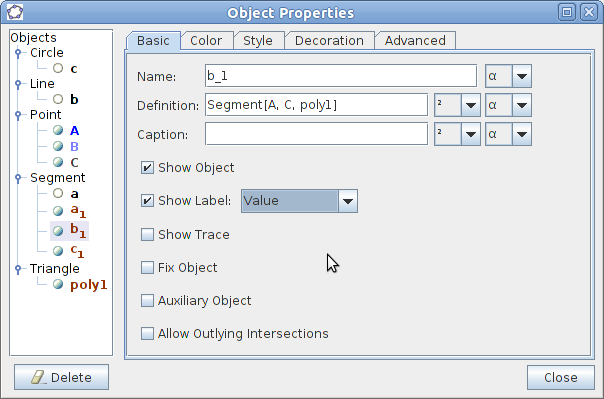
- The lengths of the sides in the triangle can be shown. Right-click one of the sides and choose Object Properties in the menu which shows up. Check the Show Label field and choose Value from the drop down list.
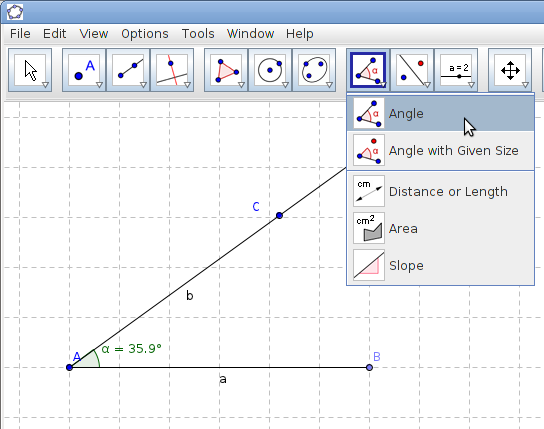
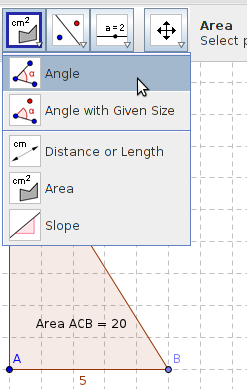 To show the size of the angles use the Angle tool. Click on each vertex of the triangle. The order in which you click the vertices must be in the clock wise direction. In this figure click in this order BAC, CBA, and ACB.
To show the size of the angles use the Angle tool. Click on each vertex of the triangle. The order in which you click the vertices must be in the clock wise direction. In this figure click in this order BAC, CBA, and ACB.
- The area of the triangle can also be shown, use the Area tool as seen in the figure above. Click on Area tool and then click on the polygon.
- Change the shape of the triangle by moving the points you are able to move (use the Move tool).
To save GeoGebra files
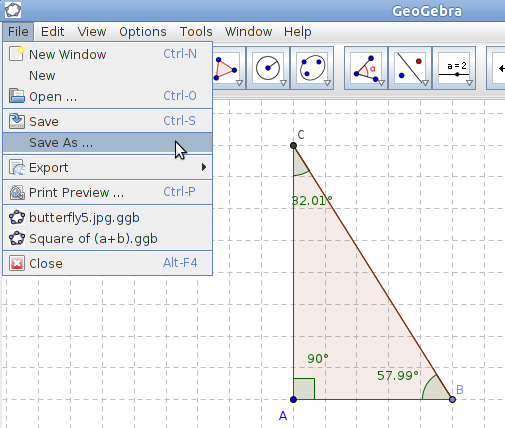
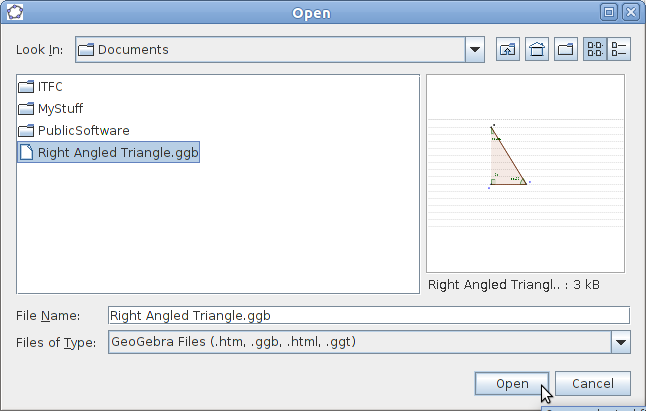
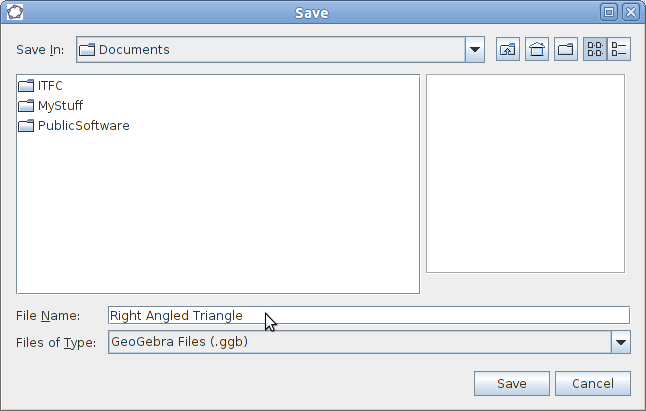 To save your GeoGebra file, select menu item File > Save As.
To save your GeoGebra file, select menu item File > Save As.- Select the Document folder.
- Type the filename Right Angled Triangle.
- The Files of Type box will automatically have Geogebra Files (.ggb).
- Click Save. Your file will be saved as Right Angled Triangle.ggb.
- Open the GeoGebra applications.
- Select menu item File > Open.
- Select the folder and the file.
- Click Open.
Additionally you can try the following exercise.
- Follow the following steps to construct a rectangle ABCD like the figure. Use the Move tool and move the vertices of the rectangle. If you have constructed the rectangle correctly, when you move the vertices the figure will always be a rectangle. Seeing this construction can you write down the properties of a rectangle? Steps:
- Draw a line segment AB of any length (Segment between two points tool).
- Draw a perpendicular line at point A perpendicular to line segment AB. For this in GeoGebra : Select the Perpendicular line tool. Click on point A then select line segment AB.
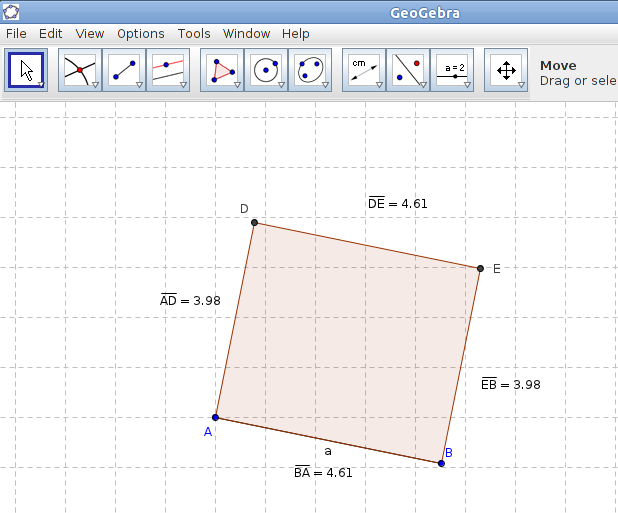
- Similarly draw another perpendicular line at point B to line segment AB. How will you do this in GeoGebra?
- Now select the 'Parallel Line tool and draw a parallel line to AB at any new point C'.
- Mark the intersection points of the parallel and perpendicular lines as D and E using the Intersect two objects tool.
- ADEB the rectangle you constructed.
- To measure the sides, use the Distance or Length tool and click on points AD, then DE, then EB and finally AB.
- Select the move tool and move points A or B. What do you observe, write down your observations.
- Now use the polygon tool and complete your rectangle. Also hide the construction. How will you do this?
Chapter summary
In this chapter you have learnt about:
- GeoGebra is a mathematical tool that helps you construct geometrical figures and see the geometric and algebraic representations at the same time. It is dynamic (where you can change the values of some of the properties like length, angle) and you can animate your geometric figures to understand properties of the figures you have drawn.
- You learnt how to use GeoGebra to construct different geometrical figures and understand some mathematical concepts.
Exercises
- Verifying a Theorem: T'he sum of the interior angles of a triangle are 180 degrees.'
- Draw three points A, B, C (New Point tool)
- Draw the triangle with vertices A,B and C (Polygon tool)
- Select the Angle tool to measure each of the interior angles of the triangle. Now verify that the sum of all the interior angles equals to 180 degrees.
- Select one of the vertices of the triangle (A,B or C) and move the points (Move tool) to change the shape of the triangles.
|
Angle BAC
|
Angle CBA
|
Angle ACB
|
Sum of Interior Angles of Triangle ABC
|
- Exploring the rule: Similar triangles are proportional : Draw a triangle. Place a point on one of the sides and draw a line through this point parallel to one of the sides in the triangle. Parallel line: Use the Parallel line tool. You now have two triangles like the figure below.
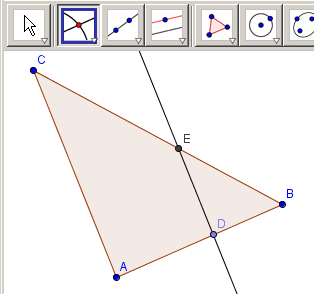
- Explain why triangle ABC is similar to triangle DBE. Measure the lengths of the sides in both triangles.
- Check if the rule stating that the ratio between the lengths of corresponding sides in similar triangles is the same applies.
- Measuring lengths: Use the Distance or Length tool.
- Make the Algebra View visible: View on the Menu Item.
- Show names of points: Right‐click on one of the points, choose properties, in the list on the left side click on points and check Show Label.
- Calculate the ratio: In the Input bar write: r1=Distance[A,B]/Distance[A,D]. AB and AD are corresponding sides in the two triangles. Repeat the command for the other two pairs of corresponding sides.
- Change the shape of the triangle by moving the points you are able to move (use the Move tool). Are the triangles still similar? What happens to the ratios?
- Construct a square in GeoGebra. You are only given a line segment AB of any length. How will you construct the square? The steps are given below
- Draw a line segment AB of any length using Segment between Two Points Tool'.'
- Draw two perpendicular lines at points A and B respectively and perpendicular to the line segment AB using Perpendicular Line tool'.'
- Draw a circle of radius = length of line segment AB using the circle with centre 'through point tool'. Make point A the centre of the circle and point B as the point on the circle.
- Use Intersection two objects and click on the point where the circle intersects the perpendicular line at A. This will be point C.
- Draw a parallel line by selecting point C and line segment AB using the parallel line tool.
- Use Intersection two objects and click on the point where the parallel line intersects the perpendicular line at B. This will be point D.
- ABCD is your square.
- Measure the sides using the Distance or Length tool. What do you observe? What are the properties of a square?
 Move the points A or B using the Move tool. Is ABCD still a square?
Move the points A or B using the Move tool. Is ABCD still a square?
Additional resources
- To learn more GeoGebra seethe website [[1]]
- To download GeoGebra files (.ggb) created by your mathematics teachers go to [[2]] Select Maths Tab , then Computer Tools Tab.
- [[3]] To see video tutorials of GeoGebra
- To learn about how to participate in mathematics olympiads please see the website [[4]]
- Here are a list of mathematics websites that you can try out puzzles