Difference between revisions of "Triangles"
| Line 144: | Line 144: | ||
These points of concurrencies, orthocenter, centroid, and circumcenter of any triangle are collinear that is they lie on the same straight line called the Euler line. | These points of concurrencies, orthocenter, centroid, and circumcenter of any triangle are collinear that is they lie on the same straight line called the Euler line. | ||
| − | =====Activities #===== | + | ======Activities #====== |
======[[Exploring concurrent lines from given surroundings]]====== | ======[[Exploring concurrent lines from given surroundings]]====== | ||
Interactive activity to introduce concurrent lines using examples from our surroundings. | Interactive activity to introduce concurrent lines using examples from our surroundings. | ||
| Line 156: | Line 156: | ||
[[Image:KOER%20Triangles_html_m404a4c0b.gif|link=]] | [[Image:KOER%20Triangles_html_m404a4c0b.gif|link=]] | ||
| − | =====Activities #===== | + | ======Activities #====== |
======[[Marking centroid of a triangle|Marking centroid of the triangle]]====== | ======[[Marking centroid of a triangle|Marking centroid of the triangle]]====== | ||
This is a hands on activity to explore concurrent lines formed in a triangle when vertices are joined to the midpoints of the opposite side. | This is a hands on activity to explore concurrent lines formed in a triangle when vertices are joined to the midpoints of the opposite side. | ||
| Line 166: | Line 166: | ||
=====Concept #: Concurrency of altitudes in triangles===== | =====Concept #: Concurrency of altitudes in triangles===== | ||
The distance between a vertex of a triangle and the opposite side is called the altitude of the triangle. Altitude also refers to the length of the segment. Altitudes can be used to compute the area of a triangle: one half of the product of an altitude's length and its base's length equals the triangle's area. A triangle has 3 altitudes. The intersecting point of 3 altitudes of a triangle is known as orthocentre of the triangle. This point may be inside, outside, or on the triangle. If the triangle is obtuse, it will be outside. If the triangle is acute, the orthocentre is inside the triangle. The orthocenter on a right triangle would be directly on the 90° vertex. From Greek: orthos - "straight, true, correct, regular" The point where the three altitudes of a triangle intersect. One of a triangle's points of concurrency. | The distance between a vertex of a triangle and the opposite side is called the altitude of the triangle. Altitude also refers to the length of the segment. Altitudes can be used to compute the area of a triangle: one half of the product of an altitude's length and its base's length equals the triangle's area. A triangle has 3 altitudes. The intersecting point of 3 altitudes of a triangle is known as orthocentre of the triangle. This point may be inside, outside, or on the triangle. If the triangle is obtuse, it will be outside. If the triangle is acute, the orthocentre is inside the triangle. The orthocenter on a right triangle would be directly on the 90° vertex. From Greek: orthos - "straight, true, correct, regular" The point where the three altitudes of a triangle intersect. One of a triangle's points of concurrency. | ||
| − | =====Activities #===== | + | ======Activities #====== |
======[[Altitudes and orthocenter of a triangle]]====== | ======[[Altitudes and orthocenter of a triangle]]====== | ||
An altitude of a triangle is a line segment that is drawn from the vertex to the opposite side and is perpendicular to the side. A triangle can have three altitudes. Point of intersection of these lines for different types of triangles is explored. | An altitude of a triangle is a line segment that is drawn from the vertex to the opposite side and is perpendicular to the side. A triangle can have three altitudes. Point of intersection of these lines for different types of triangles is explored. | ||
| Line 173: | Line 173: | ||
One consequence of the Perpendicular Bisector Theorem is that the perpendicular bisectors of a triangle intersect at a point that is equidistant from the vertices of the triangle. | One consequence of the Perpendicular Bisector Theorem is that the perpendicular bisectors of a triangle intersect at a point that is equidistant from the vertices of the triangle. | ||
| − | =====Activities #===== | + | ======Activities #====== |
[[Perpendicular bisectors and circumcenter of a triangle|'''Perpendicular bisectors and circumcenter of a triangle''']] | [[Perpendicular bisectors and circumcenter of a triangle|'''Perpendicular bisectors and circumcenter of a triangle''']] | ||
| Line 181: | Line 181: | ||
If a point is on the bisector of an angle, then it is equidistant from the two arms of the angle. | If a point is on the bisector of an angle, then it is equidistant from the two arms of the angle. | ||
| − | =====Activities #===== | + | ======Activities #====== |
======[[Angular bisectors and incenter of a triangle]]====== | ======[[Angular bisectors and incenter of a triangle]]====== | ||
The intersecting point of three lines which are the bisectors of three angles of a triangle that is the incenter and it's properties are examined. | The intersecting point of three lines which are the bisectors of three angles of a triangle that is the incenter and it's properties are examined. | ||
Revision as of 07:07, 10 May 2019
| Philosophy of Mathematics |
While creating a resource page, please click here for a resource creation checklist.
Concept Map
Additional Resources
OER
- Web resources:
- Wikipedia, the free encyclopedia : The website gives a comprehensive information on triangles from basics to in depth understanding of the topic.
- cbsemathstudy.blogspot.com : The website contains worksheets that can be downloaded. Worksheets for other chapters can also be searched for which are listed based on class.
- Books and journals
- Textbooks
- NCERT Textbooks – Class 9
- Syllabus documents
Non-OER
- Web resources:
- Bright hub education : The website describes a lesson plan for introducing triangles and lists classroom problems at the end of the lesson that can be solved for better understanding.
- CPALMS : The website contains lesson plan, activities and worksheets associated with triangles.
- UrbanPro : This website gives downloadable worksheets with problems on triangle construction.
- AglaSem Schools : This website lists important questions for math constructions.
- National Institute of Open Schooling: This website has good reference notes on concurrency of lines in a triangle for both students and teachers.
- Math Open Reference : This website gives activities that can be tried and manipulated online for topics on geometry.
- Books and journals
- Textbooks:
- Syllabus documents (CBSE, ICSE, IGCSE etc)
Learning Objectives
- Identifying a triangle and understanding its formation
- Recognizing parameters related to triangles
- Understanding different formation of triangles based on sides and angles
- Establishing relationship between parameters associated with triangles
Teaching Outlines
Concept #: Formation of a triangle, elements of a triangle and its measures
The triangle is the basic geometrical figure that allows us to best study geometrical shapes. A quadrilateral can be partitioned into two triangles, a pentagon into three triangles, a hexagon into four triangles, and so on.These partitions allow us to study the characteristics of these figures. And so it is with Euclidean geometry—the triangle is one of the very basic parts on which most other figures depend. Here we will be investigating triangles and related its properties
Activities #
Formation of a triangle
Introducing formation of a shape with least number of lines and the space enclosed by these lines form a geometric shape.The key geometric concepts that are related with this are explained.
Elements and measures in triangle
The components that make a triangle are investigated. Measuring these components gives a better understanding of properties of triangles. Relation between these components are conceptualized.
Interior and exterior angles in triangle
Interior angles are angles that are formed with in the closed figure by the adjacent sides.An exterior angle is an angle formed by a side and the extension of an adjacent side. Exterior angles form linear pairs with the interior angles.
Concept #: Types of triangles based on sides and angles
Variations in elements that make a triangle results in distinct triangles. Recognizing these variations helps in interpreting changes that are possible with in a triangle.
Activities #
Types of triangles based on sides
A triangle can be drawn with different measures of sides and these sides determine the kind of triangle formed.
Types of triangles based on angles
A triangle can be drawn with different measures of angles which also determine the kind of triangle formed.
Concept #: Theorems and properties
Properties of triangles are logically proved by deductive method. Relations ships between angles of a triangle when a triangle is formed are recognized and understood.
Activities #
Angle sum property
Interior angles of a triangle are in relation and also determine the type of angles that can forms a triangle. This also helps in determining an unknown angle measurement.
Exterior angle theorem
Interior angle and the corresponding angle form a linear pair. This exterior angle in relation to the remote interior angles and their dependencies are deducted with the theorem.
Concept #: Construction of triangles
Constructing geometric shapes to precision using a scale and a compass helps in understanding of properties of the shape. Constructing geometric shapes with minimum number of parameters enhances thinking skills.
The following constructions are based on three essential parameters that are required for construction following the SSS, SAS and ASA theorems
Activities #
Construction of a triangle with three sides
Investigating formation of a unique triangle with the given parameters as the three sides. Constriction follows SSS congruence rule.
Construction of a triangle with two sides and an angle
Construing of a triangle when two of the sides and an angle of a triangle are known and recognizing the role of the given angle, this construction follows SAS congruence rule for the given parameters.
Construction of a triangle with two angles and included side
Construction of a triangle when two angles of a triangle and a side are known and understanding the side given can only be constructed between the two angles to form a unique triangle. Construction follows ASA congruence rule.
Construction of a right angled triangle
Right angle is one of the angles of the triangle the and assimilating other parameters that are required to complete construction. Construction of a triangle based on RH congruence rule.
Construction of a triangle with a side, an angle and sum of two sides
The triangle inequality states that the sum of the lengths of any two sides of a triangle must be greater than or equal to the length of the third side. Construction of a triangle with given parameters sum of two sides and an angle follows SAS congruence rule.
Construction of a triangle with a side, an angle and difference to two sides
Difference of two sides and an angle are parameters with which a triangle construction is possible, this construction of triangle follows SAS congruence rule.
Construction of a triangle with perimeter and base angles
Constructing a unique triangle with perimeter and with other two parameters the base angles of the triangle follows construction on a triangle using SAS congruence rule.
Concept #: Concurrency in triangles
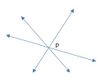
A set of lines are said to be concurrent if they all intersect at the same point. In the figure below, the three lines are concurrent because they all intersect at a single point P. The point P is called the "point of concurrency". This concept appears in the various centers of a triangle.
All non-parallel lines are concurrent.
Rays and line segments may, or may not be concurrent, even when not parallel.
In a triangle, the following sets of lines are concurrent:
The three medians.
The three altitudes.
The perpendicular bisectors of each of the three sides of a triangle.
The three angle bisectors of each angle in the triangle.
The medians, altitudes, perpendicular bisectors and angle bisectors of a triangle are all concurrent lines. Their point of intersections are called centroid, orthocentre, circumcentre and incentre respectively. Concurrent lines are especially important in triangle geometry, as the three-sided nature of a triangle means there are several special examples of concurrent lines, including the centroid, the circumcenter and the orthocenter.
These points of concurrencies, orthocenter, centroid, and circumcenter of any triangle are collinear that is they lie on the same straight line called the Euler line.
Activities #
Exploring concurrent lines from given surroundings
Interactive activity to introduce concurrent lines using examples from our surroundings.
Concept #: Concurrency of medians in triangles.
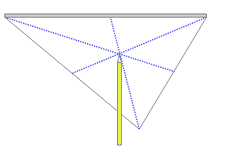
Median of a triangle is a line segment from a vertex to the midpoint of the opposite side. A triangle has three medians. Each median divides the triangle into two smaller triangles of equal area. The medians of a triangle are concurrent and the point of concurrence is called the centroid. The centroid is always inside the triangle. The centroid is exactly two-thirds the way along each median. i.e the centroid divides each median into two segments whose lengths are in the ratio 2:1, with the longest one nearest the vertex.
From Latin: centrum - "center", and Greek: -oid -"like" The centroid of a triangle is the point through which all the mass of a triangular plate seems to act. Also known as its 'center of gravity' , 'center of mass' , or barycenter. Refer to the figure . Imagine you have a triangular metal plate, and try and balance it on a point - say a pencil tip. Once you have found the point at which it will balance, that is the centroid. In the diagram, the medians of the triangle are shown as dotted blue lines.
Activities #
Marking centroid of the triangle
This is a hands on activity to explore concurrent lines formed in a triangle when vertices are joined to the midpoints of the opposite side.
Medians and centroid of a triangle
The centroid of a triangle is where the three medians intersect. This activity will show you how to find the centroid and you’ll explore several geometric relationships related to centroid and medians.
Concept #: Concurrency of altitudes in triangles
The distance between a vertex of a triangle and the opposite side is called the altitude of the triangle. Altitude also refers to the length of the segment. Altitudes can be used to compute the area of a triangle: one half of the product of an altitude's length and its base's length equals the triangle's area. A triangle has 3 altitudes. The intersecting point of 3 altitudes of a triangle is known as orthocentre of the triangle. This point may be inside, outside, or on the triangle. If the triangle is obtuse, it will be outside. If the triangle is acute, the orthocentre is inside the triangle. The orthocenter on a right triangle would be directly on the 90° vertex. From Greek: orthos - "straight, true, correct, regular" The point where the three altitudes of a triangle intersect. One of a triangle's points of concurrency.
Activities #
Altitudes and orthocenter of a triangle
An altitude of a triangle is a line segment that is drawn from the vertex to the opposite side and is perpendicular to the side. A triangle can have three altitudes. Point of intersection of these lines for different types of triangles is explored.
Concept #: Concurrency of Perpendicular bisectors in a triangle
The perpendicular bisector of a triangle is the perpendicular drawn to a line segment which divides it into two equal parts. The point where the three perpendicular bisectors of a triangle meet is called the circumcentre of a triangle. The circumcentre of a triangle is equidistant from all the three sides vertices of the triangle. This common distance is the crcumradius. The circumcentre is also the center of the triangle's circumcircle - the circle that passes through all three of the triangle's vertices. The circumcentre of a triangle lies inside or on a side or outside the triangle according as the triangle is acute or right angled or obtuse. The circumcentre of a right angled triangle is the mid-point of its hypotenuse. Latin: circum - "around" centrum - "center"
One consequence of the Perpendicular Bisector Theorem is that the perpendicular bisectors of a triangle intersect at a point that is equidistant from the vertices of the triangle.
Activities #
Perpendicular bisectors and circumcenter of a triangle
Circumcentre for different types of triangles is investigated with this activity and this further explores several geometric relationships related to the circumcentre and perpendicular bisectors.
Concept #: Concurrency of angle bisectors in triangles.
The ray which bisects an angle is called the angle bisector of a triangle. The point of concurrence of angle bisectors of a triangle is called as incentre of the triangle. The incentre always lies inside the triangle. The distance from incentre to all the sides are equal and is referred to as inradius. The circle drawn with inradius is called incircle and touches all sides of the triangle.
If a point is on the bisector of an angle, then it is equidistant from the two arms of the angle.
Activities #
Angular bisectors and incenter of a triangle
The intersecting point of three lines which are the bisectors of three angles of a triangle that is the incenter and it's properties are examined.
Concept #: Similar and congruent triangles
Two objects are similar if they have the same shape, but not necessarily the same size. This means that we can obtain one figure from the other through a process of expansion or contraction, possibly followed by translation, rotation or reflection. If the objects also have the same size, they are congruent. Two triangles are said to be congruent to one another only if their corresponding sides and angles are equal to one another